Impact of uncertain demand and lead-time reduction on two-echelon supply chain

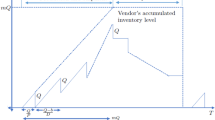
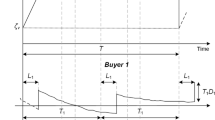
Abstract

This paper develops a continuous-review vendor-buyer supply chain (SC) model wherein the lead-time (taken as replenished) is considered as a factor affected upon by the time stamp required for setup and production followed by transportation. Here, the production time indicates the interaction between the lot-size and lead-time. Assuming the existence of an opportunity with the buyer of reducing the replenishment lead-time. The buyer receives normally distributed stochastic lead-time demands from its customers. Due to the stochastic nature of lead-time demand, shortages may arise at the buyer’s side which is fully backlogged. We presume imperfection production at the vendor’s end, which leads to the generation of a certain ratio/percentage of defective products, which results in additional warranty costs for the vendor. This study intends to uncover the best policy that minimizes the system’s total expected cost. A solution algorithm with some lemmas is provided which helped in finding the optimal solution and to prove the uniqueness of the solutions. Findings demonstrate that a reduction in lead-time can effectively lower safety stock as well as the total cost.

Appendices

Appendix A: Proof of Lemma 1

Proof

We have the second order derivative derivative of $\Pi _{sc}$ as

$$\begin{aligned} \frac{\partial ^2 \Pi _{sc}}{\partial Q^2} =L_{1}^{-3/2}\left[ L1\left\{ \frac{E_{5}}{Q^2}+ \frac{E2}{Q^2}+\frac{2(E_{4}+\sqrt{L_{1}}E_{3})}{Q^3}\right\} + \frac{1}{2P}\left( \frac{E5}{Q}+\frac{E2}{Q}+\frac{E4}{Q^2}\right) -\frac{E1}{2P}\right] \qquad \end{aligned}$$

(25)

where $E_{1}=\frac{\sigma k_{1}h_{B}}{2P}>0,$

$E_{2}=\frac{\sigma \pi D\Psi (k_{1})}{2mP(1-E[Y])}>0,$

$E_{3}=\frac{D}{1-E[Y]}\left\{ F+\frac{S_{B}+S_{V}}{m}+\left( 1-\frac{1}{m}\right) \pi \sigma \sqrt{\kappa _{t0}e^{-aW}}\Psi (k_{2})\right\} >0,$

$E_{4}=\frac{D\sigma \pi }{m(1-E[Y])}\left( \kappa _{t0}e^{-aW}+s_{t}\right) \Psi (k_{1})>0,$

$E_{5}=\frac{(m-1)\sigma \pi Dk_{1}[1-\Phi (k_{2})]}{2mP(1-E[Y])}>0.$

As the first and second terms of (25) within the bracket converge to zero for large Q, and therefore it is obvious that $\frac{\partial ^2 \Pi _{sc}}{\partial Q^2}<0$ for large value of Q,  and hence clearly $\left| \frac{\partial ^2 \Pi _{sc}}{\partial Q^2}\right| _{Q=\infty }=0.$ Therefore, $\Pi _{sc}(Q,k_{1},W,m)$ is not convex in Q.

To prove the existence of the unique solution, we consider the following.

The first-order partial derivative of $\Pi _{sc}(Q,k_{1},W,m)$ with respect to Q for given $k_{1}, W,$ and m is given by

$$\begin{aligned} \frac{\partial \Pi }{\partial Q}= & {} \left\{ -\left( \frac{S_{B}+S_{V}}{mQ^2}\right) D-\frac{FD}{Q^2}-\frac{(m-2)Dh_{V}}{2P}\right\} \left( \frac{1}{1-E[Y]}\right) \\&+\frac{h_{B}}{(1-E[Y])}\left( \frac{E[Y]D}{x}+\frac{E(1-Y)^2}{2}\right) \nonumber \\&+\frac{(m-1)}{2}h_{V}+\frac{h_{B}k_{1}\sigma }{2P\sqrt{L_{1}}}-\frac{\pi D}{mQ^2(1-E[Y])}\Bigg \{\sigma \sqrt{L_{1}}\Psi (k_{1})+(m-1)\sigma \sqrt{L_{2}}\Psi \left( k_{1}\sqrt{\frac{L_{1}}{L_{2}}}\right) \Bigg \}\nonumber \\&+\frac{\pi D}{mQ(1-E[Y])}\Bigg \{\frac{\sigma \Psi (k_{1})}{2P\sqrt{L_{1}}}-\frac{(m-1)k_{1}\sigma \left[ 1-\Phi \left( k_{1}\sqrt{\frac{L_{1}}{L_{2}}}\right) \right] }{2P\sqrt{L_{1}}}\Bigg \} \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \frac{\partial \Pi }{\partial Q}= & {} H(m)+L_{1}^{-1/2} \left( E_{1}-\frac{E_{2}}{Q}-\frac{\sqrt{E_{3}L_{1}}}{Q^2}-\frac{E_{4}}{Q^2} -\frac{E_{5}}{Q}\right) \end{aligned}$$

(26)

where $H(m)=\frac{h_{V}}{2}\left( m-1-\frac{D(m-2)}{P(1-E[Y])}\right) +\frac{h_{B}}{1-E[Y]}\left( \frac{E[(1-Y)^2]}{2}+\frac{DE[Y]}{x}\right) >0.$

In (26), the last four terms within the bracket converge to zero for large Q and it is certain that $\left| \frac{\partial \Pi }{\partial Q}\right| _{Q=\infty }=H(m)>0.$

$$\begin{aligned} \hbox {If}~\left| \frac{\partial \Pi }{\partial Q}\right| _{Q=1}= & {} H(m)+\left( \frac{1}{P}+\kappa _{t0}e^{-aW}+s_{t}\right) ^{-1/2}\\&\left( E_{1}-E_{2}-\sqrt{E_{3}\left( \frac{1}{P}+\kappa _{t0}e^{-aW}+s_{t}\right) }-E_{4}-E_{5}\right) \ge 0 \end{aligned}$$

then $\frac{\partial \Pi }{\partial Q}\ge 0$ for all Q which implies that $\Pi _{sc}$ is a strictly increasing function of Q and the optimal solution is the possible minimum lot size $Q_{min}$.

$$\begin{aligned} \hbox {If}~\left| \frac{\partial \Pi }{\partial Q}\right| _{Q=1}= & {} H(m)+\left( \frac{1}{P}+\kappa _{t0}e^{-aW}+s_{t}\right) ^{-1/2}\\&\left( E_{1}-E_{2}-\sqrt{E_{3}\left( \frac{1}{P}+\kappa _{t0}e^{-aW}+s_{t}\right) } -E_{4}-E_{5}\right) <0 \end{aligned}$$

then it is clear that the sign of the first-order partial derivative changes from negative to positive only once for $1\le Q<\infty .$ This means that $\frac{\partial \Pi _{sc}}{\partial Q}=0$ has a unique solution for fixed $k_{1},W,$ and m. The sign of the first-order derivative indicates that $\Pi _{sc}$ gradually increases after a point of inflection. Thus, for fixed $k_{1},W,$ and m, there exists an optimal solution that can be determined uniquely in Q.

Hence, Lemma 1 is proved. $\square$

Appendix B: Proof of Lemma 2

Proof

Now, evaluating first and second order partial derivatives of $\Pi _{sc}$ w.r.t. $k_{1}$:

$$\begin{aligned} \frac{\partial \Pi _{sc}}{\partial k_{1}}= & {} h_{B}\sigma \sqrt{L_{1}}-\frac{\pi D\sigma }{mQ}\left\{ 1-\Phi (k_{1})+(m-1)\left[ 1-\Phi \left( k_{1}\sqrt{\frac{L_{1}}{L_{2}}}\right) \right] \right\} \sqrt{L_{1}} \end{aligned}$$

(B1)

and

$$\begin{aligned} \frac{\partial ^2 \Pi _{sc}}{\partial k_{1}^2}= & {} \frac{\pi D\sigma }{mQ}\left[ \phi (k_{1})+(m-1)\sqrt{\frac{L_{1}}{L_{2}}}\phi \left( k_{1}\sqrt{\frac{L_{1}}{L_{2}}}\right) \right] \sqrt{L_{1}} \end{aligned}$$

(B2)

Since $\frac{\partial ^2 \Pi _{sc}}{\partial k_{1}^2}>0$, we can conclude that the cost function $\Pi _{sc}$ is convex w.r.t. $k_{1}.$ Hence, Lemma 2 is proved. $\square$