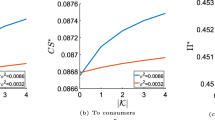
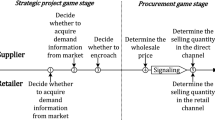
Abstract
Many upstream brand manufacturers have established their direct channels to compete with the retailers; this is encroachment behavior by the manufacturers. In this paper, we introduce the retailer’s risk-averse behavior into the manufacturer’s encroachment problem under asymmetric information, focusing specifically on how the risk-averse behavior of the retailer and the per-unit selling cost of the manufacturer influence the optimal decisions. To address this problem, we assume that the market demand may be high or low, and each kind of demand follows a truncated normal distribution. The retailer has more information regarding the market size than the manufacturer. Under the mean–variance decision framework, we develop a dual-channel supply chain model and obtain three feasible regions of the optimal equilibrium results. We find that whether the profit of the manufacturer and the utility of the retailer are better off or worse off depends on the manufacturer’s per-unit selling cost and the degree of risk aversion of the retailer. Numerical experiments provide the comparisons of the expected profits and the utilities of both members in the supply chain under asymmetric information and symmetric information.






Similar content being viewed by others
References
Arya, A., Mittendorf, B., & Sappington, D. E. M. (2007). The bright side of supplier encroachment. Marketing Science, 26(5), 651–659.
Babich, V., Li, H., Ritchken, P., & Wang, Y. (2012). Contracting with asymmetric demand information in supply chains. European Journal of Operational Research, 217(2), 333–341.
Burnetas, A., Gilbert, S. M., & Smith, C. E. (2007). Quantity discounts in single-period supply contracts with asymmetric demand information. IIE Transactions, 39(5), 465–479.
Cachon, G. P., & Lariviere, M. A. (2001). Contracting to assure supply: How to share demand forecasts in a supply chain. Management Science, 47(5), 629–646.
Choi, T. M., Li, D., & Yan, H. (2008). Mean–variance analysis of a single supplier and retailer supply chain under a returns policy. European Journal of Operational Research, 184(1), 356–376.
Feng, Q., Lai, G., & Lu, L. X. (2014). Dynamic bargaining in a supply chain with asymmetric demand information. Management Science. doi:10.1287/mnsc.2014.1938.
Gan, X., Sethi, S. P., & Yan, H. (2005). Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer. Production and Operations Management, 14(1), 80–89.
Gümüş, M. (2014). With or without forecast sharing: Competition and credibility under information asymmetry. Production and Operations Management, 23(10), 1732–1747.
Kalkanci, B., Chen, K. Y., & Erhun, F. (2011). Contract complexity and performance under asymmetric demand information: An experimental evaluation. Management Science, 57(4), 689–704.
Karray, S. (2014). Modeling brand advertising with heterogeneous consumer response: Channel implications. Annals of Operations Research. doi:10.1007/s10479-014-1656-9.
Lai, G., Xiao, W., & Yang, J. (2012). Supply chain performance under market valuation: An operational approach to restore efficiency. Management Science, 58(10), 1933–1951.
Lau, H. S., & Lau, A. H. L. (1999). Manufacturer’s pricing strategy and return policy for a single-period commodity. European Journal of Operational Research, 116(2), 291–304.
Li, B., Chen, P., Li, Q., & Wang, W. (2014a). Dual-channel supply chain pricing decisions with a risk-averse retailer. International Journal of Production Research, 52(23), 7132–7147.
Li, Z., Gilbert, S., & Lai, G. (2013). Supplier encroachment under asymmetric information. Management Science, 60(2), 449–462.
Li, Y., Lin, Q., & Ye, F. (2014b). Pricing and promised delivery lead time decisions with a risk-averse agent. International Journal of Production Research, 52(12), 3518–3537.
Liu, Y., & Zhang, Z. J. (2006). Research note—The benefits of personalized pricing in a channel. Marketing Science, 25(1), 97–105.
Loch, C. H., & Wu, Y. Z. (2008). Social preferences and supply chain performance: An experimental study. Management Science, 54(11), 1835–1849.
Ma, L., Liu, F., Li, S., & Yan, H. (2012). Channel bargaining with risk-averse retailer. International Journal of Production Economics, 139(1), 155–167.
Markowitz, H. M. (1959). Porfolio selection: Efficient diversification of investment. New York: Wiley.
Özer, Ö., Zheng, Y., & Ren, Y. (2014). Trust, trustworthiness, and information sharing in supply chains bridging China and the United States. Management Science, 60(10), 2435–2460.
Porteus, E. L., & Whang, S. (1999). Supply chain contracting: Nonrecurring engineering charge, minimum order quantity and boilerplate contracts. Stanford: Stanford University.
Tsay, A. A. (2002). Managing retail channel overstock: Markdown money and return policies. Journal of Retailing, 77(4), 457–492.
Wang, C. X., & Webster, S. (2007). Channel coordination for a supply chain with a risk-neutral manufacturer and a loss-averse retailer. Decision Sciences, 38(3), 361–389.
Wei, Y., & Choi, T. M. (2010). Mean–variance analysis of supply chains under wholesale pricing and profit sharing schemes. European Journal of Operational Research, 204(2), 255–262.
Xu, G., Dan, B., Zhang, X., & Liu, C. (2014). Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract. International Journal of Production Economics, 147, 171–179.
Acknowledgments
The authors gratefully acknowledge reviewers for their constructive comments and suggestions that were instrumental in improving this paper. This work is supported by the Program for the Humanity and Social Science Foundation of the Ministry of Education, China, No. 12YJAZH052 and the National Nature Science Foundation of China under Grant No. 71472133.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 2 and Proposition 1
When the information is symmetric, the retailer has not mimicking incentives, the optimal order quantity follows \(q_R (w;i)=\frac{\mu _i -2w+c-k\sigma }{2}\) (it is positive because of\(w<\frac{\mu _i +c-k\sigma }{2})\). \(\forall i,j\in \{H,L\}\), \(i\ne j\), the retailer’s utility function is
Similarly, we have \(V_{ii} (q_R )=\frac{1}{2}\left[ {\mu _i -q_R (w;i)+c-2w-k\sigma } \right] q_R (w;i)\), \(\forall i\in \{H,L\}\). \(\square \)
Obviously, we have
Then, we can obtain \(V_{HL} \left( \frac{\mu _L -2w+c-k\sigma }{2}\right) \le \frac{1}{8}\left( {\mu _H -2w+c-k\sigma } \right) ^{2}\) and
It is obvious that, if \(V_{HL} \left( {\frac{\mu _L -2w+c-k\sigma }{2}} \right) \le V_{HH} \left( {\frac{\mu _H -2w+c-k\sigma }{2}} \right) \), then the retailer that observes a high market size has no incentive to mimic the ordering decision under a low market size. (Note that the retailer will never mimic the decision under a high market size, when the true market size is low). The condition can be written as \(w\ge \overline{{w}}=\frac{3\mu _L -\mu _H +2c-2k\sigma }{4}\). Then, the next condition is satisfied, \(V_{HL} \left( {\frac{\mu _L -2w+c-k\sigma }{2}} \right) >V_{HH} \left( {\frac{\mu _H -2w+c-k\sigma }{2}} \right) \), or identically, \(w<\overline{{w}}\); then the retailer who observes a high market size may attempt to mimic the ordering decision under a low market size. Consequently, for a separating equilibrium to hold, the retailer, when observing a low market size, must downward distort order quantity to a level such that he would have no incentive to mimic when observing a high market size, i.e.,
By expanding the condition
we obtain the threshold order quantity is
where \(B=\left( {\mu _H -\mu _L } \right) \left( {3\mu _H -\mu _L -4w+2c-2k\sigma } \right) \).
We can verify that

where  and the manufacturer’s quantity \(q_M (w;i)=\frac{\mu _i -q_R (w;i)-c}{2}\). In conclusion, a separating equilibrium is constituted.
and the manufacturer’s quantity \(q_M (w;i)=\frac{\mu _i -q_R (w;i)-c}{2}\). In conclusion, a separating equilibrium is constituted.
Proof of Proposition 2
When \(w\ge \overline{{w}}\), the retailer will not deceive the manufacturer and thus \(q_R (w;i)=\frac{\mu _i -2w+c-k\sigma }{2}\). The manufacturer’s optimal expected profit in the natural separating equilibrium is (NS denotes natural separating, i.e., without distortion):
When \(w\le \overline{{w}}\), the retailer distorts his order quantity when the market size is low and thus \(q_R (w;L)=\overline{{q}}_R (w)\). The optimal expected profit of the manufacturer is (SD denotes separating with distortion):
\(\square \)
The manufacturer sets the best wholesale price according to the above two types of separating equilibrium; that is to say, the manufacturer can choose the better results by solving the next two programs with constraint.
The first order condition of \(E\left[ {\prod \nolimits _M^{NS} (w)} \right] \) reduces to the unconstrained optimal solution
The first derivative of \(E[ {\prod \nolimits _M^{SD} (w)} ]\) follows
where \(\frac{M}{N}=\frac{\sqrt{\mu _H -\mu _L }}{\sqrt{3\mu _H -\mu _L +2c-4w-2k\sigma }}\), which yield the first order condition
The first-order condition of \(\overline{{q}}_R (w)\) is
where \(C=\left( {\mu _H -\mu _L } \right) \left( {\mu _H -\mu _L +2(\mu _H -2w+c)-2k\sigma } \right) =M^{2}N^{2}\).
According to the condition \(\frac{\sqrt{\mu _H -\mu _L }}{\sqrt{3\mu _H -\mu _L +2c-4w-2k\sigma }}=\frac{M}{N}=\frac{M}{\sqrt{G+M^{2}}}\), where \(G=2(\mu _H -2w+c-k\sigma )\), when \(w<\overline{{w}},\overline{{w}}=\frac{1}{4}\left( {3\mu _L -\mu _H +2c-2k\sigma } \right) ,G>3\left( {\mu _H -\mu _L } \right) >0\), then \(0<\frac{M}{N}<1\).
The solution of (23) is \(w_f =\frac{\mu _H +2\mu _L -c-k\sigma }{6}\) when \(\lambda =0\), and \(w_f =\frac{1}{6}\left( {3\mu _H -c-k\sigma } \right) \) when \(\lambda =1\), where \(\frac{M}{N}=\frac{\sqrt{\mu _H -\mu _L }}{\sqrt{3\mu _H -\mu _L +2c-4w-2k\sigma }}\).
Notice that when \(w<\overline{{w}}\), which implies \(0<1-\frac{M}{N}<1\). One can be shown by the implicit function theorem that \(w_f \) increases in \(\lambda \). Thus, for \(\frac{dE[ {\prod \nolimits _M^{NS} (w)} ]}{dw}=0\) to hold for \(w_f <\overline{{w}}\), we must have \(3\mu _H -c-k\sigma -6w_f >0\) and \(\mu _H +2\mu _L -c-k\sigma -6w_f <0\) (given \(3\mu _H -c-k\sigma >\mu _H +2\mu _L -c-k\sigma \)).
Then,
Due to \(\frac{dE[ {\prod \nolimits _M^{SD} (w)} ]}{dw}<0\), that is to say,
Then we obtain that if \(\frac{dE[ {\prod \nolimits _S^{NS} (w)} ]}{dw}=0\) has a solution \(w_f \in (0,\overline{{w}})\), which asserts that the unconstrained maximizer, \(w_f \), of \(E[ {\prod \nolimits _M^{SD} (w)} ]\) must be larger than \(\frac{3\mu -c-k\sigma }{6}\) i.e., the unconstrained maximizer of \(E[ {\prod \nolimits _M^{NS} (w)} ]\). Note that we can derive the second and third derivatives of \(E[ {\prod \nolimits _M^{SD} (w)} ]\). In particular, the third derivative \(\frac{d^{3}E[ {\prod \nolimits _M^{SD} (w)} ]}{dw^{3}}\) is always positive when \(w\le \overline{{w}}\) and thus the second derivative \(\frac{d^{2}E[ {\prod \nolimits _M^{SD} (w)} ]}{dw^{2}}\) is increasing when \(w\le \overline{{w}}\). Therefore, there at most exists one solution of \(\frac{dE[ {\prod \nolimits _M^{SD} (w)} ]}{dw}=0\) in \((0,\overline{{w}})\).
Note that \(E[ {\prod \nolimits _M^{NS} (w)} ]\) and \(E[ {\prod \nolimits _M^{SD} (w)} ]\) coincide at \(w=\overline{{w}}\) because the retailer’s order quantity in the equilibrium without distortion coincides with that with distortion at \(w=\overline{{w}}\). Therefore, if \(\overline{{w}}\le w^{NS*}=\frac{3\mu -c-k\sigma }{6}\), or identically, \(c\le \frac{3( {1+2\lambda } )(\mu _H -\mu _L )+4k\sigma }{8}\), then \(w^{NS*}\) induces a natural separating equilibrium; moreover, \(E[ {\prod \nolimits _S^{SD} (w)} ]\) must be increasing at \(w=\overline{{w}}\) given that \(E[ {\prod \nolimits _M^{SD} (w)} ]\) is increasing at \(w=0\) and any solution of the first order condition of \(E[ {\prod \nolimits _M^{SD} (w)} ]\) is larger than \(w^{NS*}\) or \(\overline{{w}}\). Hence, if \(c\le \frac{3( {1+2\lambda } )(\mu _H -\mu _L )+4k\sigma }{8}\), \(\overline{{w}}<w^{NS*}\), \(w^{AI}=w^{NS*}=\frac{3\mu -c-k\sigma }{6}\) is the manufacturer’s optimal wholesale price. In contrast, if \(\overline{{w}}>w^{NS*}\), or identically, \(c>\frac{3( {1+2\lambda } )(\mu _H -\mu _L )+4k\sigma }{8}\), then \(w^{NS*}\) does not induce a natural separating equilibrium and the corner solution \(\overline{{w}}\) would be the manufacturer’s best choice for achieving a natural separating equilibrium. Note that if \(\frac{dE[ {\prod \nolimits _M^{SD} (w)} ]}{dw}=0\) has a solution \(w_f \in (0,\overline{{w}})\), then \(w_f \) induces the distorted separating equilibrium which is the optimal solution. If \(\frac{dE[ {\prod \nolimits _M^{SD} (w)} ]}{dw}=0\) does not have a solution in \((0,\overline{{w}})\), then \(E[ {\prod \nolimits _M^{SD} (w)} ]\) must be increasing in \((0,\overline{{w}})\) and the corner solution \(\overline{{w}}\) will be the manufacturer’s optimal wholesale price. Given the optimal wholesale price, we can directly obtain the retailer’s order quantity and then the manufacturer’s direct selling quantity.
Notice that given the optimal wholesale price \(w^{AI}=\frac{3\mu -k\sigma -c}{6}\) in the separating equilibrium without distortion, the manufacturer’s optimal expected profit can be derived as:
where \(D=\lambda (\mu _H -\mu )^{2}+(1-\lambda )(\mu _L -\mu )^{2}=\lambda \mu _H ^{2}+(1-\lambda )\mu _L ^{2}-\mu ^{2}\). The manufacturer’s expected profit in the separating equilibrium with distortion cannot be explicitly expressed.
The last step is to characterize the boundary conditions such that the manufacturer’s and the retailer’s selling quantities are strictly positive. If the manufacturer’s selling cost is low, the retailer’s selling quantity under a low market size will first go to zero. This always happens in a natural separating equilibrium, i.e., when \(c\le \frac{3\left( {1+2\lambda } \right) (\mu _H -\mu _L )+4k\sigma }{8}\) (when the retailer’s order quantity goes to zero under a low market size, the retailer would never mimic such an ordering decision when the market size is high; thus, it must be a separating equilibrium without distortion). It can be easily shown that when \(c>\frac{3\left( {1+2\lambda } \right) (\mu _H -\mu _L )+4k\sigma }{8}\), the retailer’s order quantity is positive. On the contrary, as the manufacturer’s selling cost increases, the manufacturer’s direct selling quantity may go to zero. Given \(\mu _H \) and \(\mu _L \), we define the smallest threshold \(\overline{{c}}(\lambda )\) that can be implicitly determined at which the manufacturer’s direct selling quantity goes to zero under at least one market size.
Proof of Part (i) The manufacturer can also choose a wholesale price such that the retailer does not place a low market size order. The manufacturer’s optimal expected profit in this case is
The retailer’s expected utility is
There exists a unique maximizer \(w^{AI}=\frac{3\mu _H -k\sigma -c}{6}\) and the subgame equilibrium follows directly: \(q_R^{AI} (H)=\frac{4c}{3},q_R^{AI} (L)=0\).
When \(c\in \left( {\max \left\{ {\frac{-3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4},0} \right\} ,\frac{3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4}} \right) \), the optimal expected utility of the retailer is \(U_R^{AI} =\frac{2c}{9}\lambda k\sigma -\frac{4c}{3}k\sigma \sqrt{\lambda }\) and the optimal expected profit of the manufacturer is
In Region \(R_1 \), the optimal expected utility of the retailer is
In Region \(R_2 \), the retailer’s optimal expected utility is
Proof of Proposition 3
We first show that in Region \(R_1 \), whether the manufacturer will benefit or hurt from encroachment depends on additional conditions c and k. In this region, with encroachment, the natural separating equilibrium arises and we can obtain the manufacturer’s expected profit. From Sect. 2.1, we know that without encroachment, the manufacturer’s optimal expected profit is \(\prod \nolimits _M^N =\frac{\left( {\mu -k\sigma } \right) ^{2}}{8}\) with the presumption that \(0<k<\frac{2\mu _L -\mu }{\sigma }\,\psi \) (the retailer is induced to order a positive quantity in both market scenarios).
Thus, we derive:
Let \(h_1 =\frac{3}{56}\left( {8\mu +\frac{16}{3}k\sigma } \right) -E\), where
Second, when we investigate Region \(R_2 \), we obtain the following results. By solving \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N >0\), the feasible range of c is \(c>\frac{3}{56}\left( {8\mu +\frac{16}{3}k\sigma } \right) +E\) or \(0\le c\le \max \{h_1 ,0\}\); that is, in this range, the manufacturer will benefit from encroachment under this situation. Correspondingly, if \(\max \{h_1 ,0\}<c<h_2 \), where \(h_2 =\frac{3}{56}\left( {8\mu +\frac{16}{3}k\sigma } \right) +E\), we obtain \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N <0\); in other words, the manufacturer will hurt from encroachment under this situation. \(\square \)
In the next section, we investigate Region \(R_1 \), we derive that
By solving \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N =0\), we obtain \(c=g_1 \) or \(c=g_2 \), where
In Region \(R_1 \), we obtain the following result. If \(c<g_1 \) or \(c>g_2 \), \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N >0\). Otherwise, \(g_1 <c<g_2 \), then we obtain \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N <0\).
Proof of Proposition 4
Notice that with manufacturer encroachment, in Region \(R_1 \), the retailer’s optimal expected utility is
In Region \(R_2 \), the optimal expected utility of the retailer \(U_R^{AI} \) is
In feasible Region \(R_2 \), when all the parameters are fixed except \(c, \frac{\partial U_R^{AI} }{\partial c}=\frac{1}{9}(4c-5k\sigma )\). For any given k, when \(c>\frac{5}{4}k\sigma , U_R^{AI} \) increases in c. When \(c<\frac{5}{4}k\sigma , U_R^{AI} \) decreases in c. When \(c=\frac{5}{4}k\sigma , U_R^{AI} \) achieve the maximum value. \(\square \)
The retailer’s optimal expected utility without manufacturer encroachment \(U_R^N \) is
which is independent of c.
Comparing (40) and (42), we obtain
which yields a threshold
where the two utilities of the retailer are equal; in the same manner, comparing (41) with (42) generates another threshold \(c_R^h (\lambda )\), which is an implicit function of \(\lambda \). If \(\max \left\{ {\frac{-3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4},\frac{k\sigma }{2}} \right\} <c_R^l (\lambda )\le \min \left\{ {\frac{3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4},3\mu _H -k\sigma ,\frac{3\mu _H +k\sigma }{5}} \right\} \), the retailer is worse off in \(c\in \left( {\max \left\{ {\frac{-3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4},\frac{k\sigma }{2}} \right\} ,c_R^l (\lambda )} \right] \) and better off in \(c\in \left( {c_R^l (\lambda ),\;\min \left\{ {\frac{3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4},3\mu _H -k\sigma ,\frac{3\mu _H +k\sigma }{5}} \right\} } \right] \); otherwise, if \(c_R^h (\lambda )<b\), then the retailer is worse off when the manufacturer’s per-unit selling cost \(c\in \left( {\left. {\max \left\{ {\frac{2k\sigma +3\lambda (\mu _H -\mu _L )}{4},\frac{3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4}} \right\} ,c_R^h (\lambda )} \right] } \right. \) and better off in \(c\in \left( {\left. {c_R^h (\lambda ),b} \right] } \right. \). In conclusion, whether the retailer is better off or worse off by manufacturer encroachment depends on the limitative range of c and k. Based on the above results, we obtain a threshold \(c_R (\lambda )\) that is either \(c_R^l (\lambda )\), \(c_R^h (\lambda )\) or b. The threshold \(c_R (\lambda )\) exists such that the retailer is worse off in the expectation utility with manufacturer encroachment when c satisfy the condition: \(c\in \left( {\max \left\{ {\frac{2k\sigma +3\lambda (\mu _H -\mu _L )}{4},\frac{3\sqrt{\lambda }(\mu _H -\mu _L )+2k\sigma }{4}} \right\} ,c_R (\lambda )} \right) \) and the retailer is better off when \(c\in \left( {c_R (\lambda ),b} \right) \).
Proof of Remark 1
In Region \(R_3 \), the manufacturer may be better off or worse off when the retailer distorts the order quantity downward. Because there is not closed-form solution for the manufacturer’s optimal wholesale price in a low-sized market, it is technically challenging to derive the necessary and sufficient condition under which the manufacturer is better off or worse off. Thus, we analyze the simple limiting case with \(\lambda \rightarrow 0\), then obtain the following results.
The manufacturer’s profit is \(\prod \nolimits _M^N =\frac{\left( {\mu _L -k\sigma } \right) ^{2}}{8}\) without encroachment, and the retailer’s utility \(U_R^N \) is
The manufacturer’s optimal wholesale price is
where \(\overline{w} =\frac{1}{4}\left( {3\mu _L -\mu _H +2c-2k\sigma } \right) .\) We obtain the following results:
When k takes different values, the difference between \(E[ {\prod \nolimits _M^{SD} (w)} ]\) with \(\prod \nolimits _M^N \), i.e., \(\prod \nolimits _M^{AI} -\prod \nolimits _M^N =E[ {\prod \nolimits _M^{SD} (w^{AI})} ]-\prod \nolimits _M^N >0\) or \(E[ {\prod \nolimits _M^{SD} (w^{AI})} ]-\prod \nolimits _M^N <0\). Given that the two parties’ profit functions are continuous in \(\lambda \), because of \(\mu _H \), \(\mu _L \), \(\lambda >0\), in Region \(R_3 \), we obtain that whether both parties are better off or worse off depends on the range of c and the different values k takes for a manufacturer’s encroachment. \(\square \)
Rights and permissions
About this article
Cite this article
Li, Q., Li, B., Chen, P. et al. Dual-channel supply chain decisions under asymmetric information with a risk-averse retailer. Ann Oper Res 257, 423–447 (2017). https://doi.org/10.1007/s10479-015-1852-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-1852-2