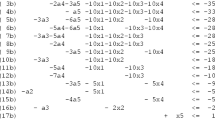Abstract
In this paper, we study the single-item and the multi-item capacitated lot sizing problem in presence of inventory bounds (CLSP-IB). That is, in any period, both the quantity produced and the stock on hand are limited. For the single-item CLSP-IB with a stationary production capacity, time-dependent inventory bounds and concave costs, we show that the problem can be solved in time \(O(T^4)\) by adapting a well-known algorithm in the literature. Restricting to non-speculative costs, we propose an \(O(T^3)\) time dynamic programming algorithm. For the multi-item CLSP-IB, we consider the lot-sizing problem with item dedicated machines and a common capacitated storage space shared by all the items. We show that this problem is \(\text{ NP }\)-hard in the strong sense even if all the cost parameters and capacities of the instance are stationary and identical for each item.





Similar content being viewed by others
References
Akbalik, A., Kebe, S., Penz, B., & Sbihi, N. (2008). Exact methods and a heuristic for the optimization of an integrated replenishment-storage planning problem. International Transactions in Operations Research, 15, 195–214.
Akbalik, A., Penz, B., & Rapine, C. (2015). Multi-item uncapacitated lot sizing problem with inventory bounds. Optimization Letters, 9(1), 143–154.
Atamturk, A., & Kucukyavuz, S. (2005). Lot sizing with inventory bounds and fixed costs: Polyhedral study and computation. Operations Research, 53, 711–730.
Atamturk, A., & Kucukyavuz, S. (2008). An \(O(n^2)\) algorithm for lot sizing with inventory bounds and fixed costs. Operations Research Letters, 36, 297–299.
Baker, K. R., Dixon, P., Magazines, M. J., & Silver, E. A. (1978). An algorithm for the dynamic lot-size problem with time-varying production capacity constraints. Management Science, 24(16), 1710–1720.
Bitran, G. R., & Yanasse, H. H. (1982). Computational complexity of the capacitated lot size problem. Management Science, 28(10), 1174–1186.
Buschkühl, L., Sahling, F., Helber, S., & Tempelmeier, H. (2010). Dynamic capacitated lot-sizing problems: A classification and review of solution approaches. OR Spectrum, 32(2), 231–261.
Chen, W. H., & Thizy, J. M. (1990). Analysis of relaxations for the multi-item capacitated lotsizing problem. Annals of Operations Research, 26, 29–72.
Chu, C., Chu, F., Zhong, J., & Yang, S. (2013). A polynomial algorithm for a lot-sizing problem with backlogging, outsourcing and limited inventory. Computers and Industrial Engineering, 64, 200–210.
Florian, M., & Klein, M. (1971). Deterministic production planning with concave costs and capacity constraints. Management Science, 18(1), 12–20.
Florian, M., Lenstra, J. K., & Rinnooy Kan, A. H. G. (1980). Deterministic production planning: Algorithms and complexity. Management Science, 26(7), 669–679.
Garey, M. R., & Johnson, D. S. (1979). Computers and intractability : A guide to the theory of NP-completeness. New York: W.H. Freeman.
Guan, Y., & Liu, T. (2010). Stochastic lot-sizing problem with inventory-bounds and constant order-capacities. European Journal of Operational Research, 207, 1398–1409.
Hwang, H.-C., & van den Heuvel, W. (2012). Improved algorithms for a lot-sizing problem with inventory bounds and backlogging. Naval Research Logistics, 59(3–4), 244–253.
Hwang, H.-C., van den Heuvel, W., & Wagelmans, A. P. M. (2013). The economic lot-sizing problem with lost sales and bounded inventory. IIE Transactions, 45, 912–924.
Jaruphongsa, W., Cetinkaya, S., & Lee, C.-Y. (2004). Warehouse space capacity and delivery time window considerations in dynamic lot-sizing for a simple supply-chain. International Journal of Production Economics, 92, 169–180.
Levi, R., Lodi, A., & Sviridenko, M. (2008). Approximation algorithms for the capacitated multi-item lot-sizing problem via flow-cover inequalities. Mathematics of Operations Research, 33(2), 461–474.
Love, S. F. (1973). Bounded production and inventory models with piecewise concave costs. Management Science, 20(3), 313–318.
Minner, S. (2009). A comparison of simple heuristics for multi-product dynamic demand lot-sizing with limited warehouse capacity. International Journal of Production Economics, 118, 305–310.
Onal, M., van den Heuvel, W., & Liu, T. (2012). A note on “Economic lot sizing problem with inventory bounds”. European Journal of Operational Research, 223(1), 290–294.
Pochet, Y., & Wolsey, L. A. (1993). Lot-sizing with constant batches: Formulation and valid inequalities. Mathematics of Operations Research, 18(4), 767–785.
Sedeno-Noda, A., Gutiérrez, J., Abdul-Jalbar, B., & Sicilia, J. (2004). An \(O(T log(T))\) algorithm for the dynamic lot size problem with limited storage and linear costs. Computational Optimization and Applications, 28, 311–323.
Toczylowski, E. (1995). An \(O(T^2)\) algorithm for the lot-sizing problem with limited inventory levels. IEEE Symposium on Emerging Technologies and Factory Automation, 3, 78–85.
van den Heuvel, W., Gutiérrez, J. M., & Hwang, H.-C. (2011). Note on An efficient approach for solving the lot-sizing problem with time-varying storage capacities. European Journal of Operational Research, 213, 455–457.
van Hoesel, C. P. M., & Wagelmans, A. P. M. (1996). An \(O(T^3)\) algorithm for the economic lot-sizing problem with constant capacities. Management Science, 42(1), 142–150.
Van Vyve, M. (2007). Algorithms for single-item lot-sizing problems with constant batch size. Mathematics of Operations Research, 32(3), 594–613.
Wagelmans, A., van Hoesel, S., & Kolen, A. (1992). Economic lot sizing: An \(O(nlogn)\) algorithm that runs in linear time in the Wagner–Whitin case. Operations Research, 40(1), 145–156.
Wagner, H. M., & Whitin, T. M. (1958). Dynamic version of the economic lot size model. Management Science, 5(1), 89–96.
Wolsey, L. A. (2006). Lot-sizing with production and delivery time windows. Mathematical Programming Series A, 107, 471–489.
Author information
Authors and Affiliations
Corresponding author
Appendix: Illustrative example for the complexity reduction
Appendix: Illustrative example for the complexity reduction
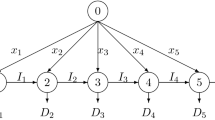
We give an example to show the idea of the reduction theoretically explained above. We consider \(n=6, T=n+1=7, P=\frac{n(n+1)}{2}=21\). The subsets \(S\) are given as follows: \(S_1=\{x_1,x_2,x_3\}, S_2=\{x_2,x_3,x_4\}, S_3=\{x_3,x_4,x_5\}, S_4=\{x_4,x_5,x_6\}, S_5=\{x_1,x_2,x_6\}, S_6=\{x_1,x_5,x_6\}\)
The two sets of items are considered as: \(A_1,\ldots ,A_6\) and \(F_1,\ldots ,F_6\). We give in Fig. 6 the demand configuration of items \(A\).
We observe that at the end of each period \(i\), there is a positive storage quantity \(P-\frac{i(i+1)}{2}\) in the warehouse. Those quantities must be stored in order to satisfy the demand exceeding the production capacity in periods \(i+1\). The stored quantities of items A are shown in Fig. 7.
The storage space is recomputed for each period and the new values are given in Fig. 8. One can easily deduce that items A are produced at full production capacity over seven periods with a total cost of \(n(n+1)=6.7=42\).
Concerning the items \(F_i\), demand configurations are given in Fig. 9 and the data is as follows:
We remark that in order to satisfy the demand of each \(F_i\) over periods 1–6, one has to produce those items in periods \(\{1,\ldots ,6\}\) (see Lemma 2). The latter has a cost of \(n^2=36\). The question asked by the instance is to know if a production policy with a cost at most \(Z=2n^2 + \frac{5n}{3}\) exists. For this example, \(Z=82\) for \(n=6\). We have already a total cost of 78. Thus, in an optimal solution we can make at most four setups in period 7 for all items F. We have to anticipate the demand of at least 2 items from the period 7 to the previous periods. However, we are constrained by the storage space: we can only anticipate at most 2 items demand. This corresponds to the search of an exact cover. Some covers are for example: \((F_1 \, \hbox {and} \, F_4)\) or \((F_2 \, \hbox {and} \, F_6)\) or \((F_3 \, \hbox {and} \, F_5)\).
Rights and permissions
About this article
Cite this article
Akbalik, A., Penz, B. & Rapine, C. Capacitated lot sizing problems with inventory bounds. Ann Oper Res 229, 1–18 (2015). https://doi.org/10.1007/s10479-015-1816-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-015-1816-6