Error analysis of the SAV Fourier-spectral method for the Cahn-Hilliard-Hele-Shaw system | Advances in Computational Mathematics
Skip to main content
Springer Nature Link
Log in

Error analysis of the SAV Fourier-spectral method for the Cahn-Hilliard-Hele-Shaw system

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

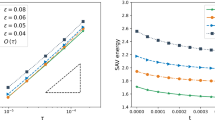
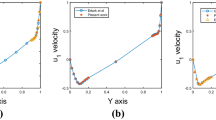
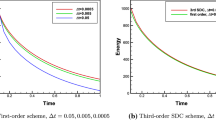
In this paper, we construct several efficient scalar auxiliary variable (SAV) schemes based on the Fourier-spectral method in space for the Cahn-Hilliard-Hele-Shaw system. The temporal discretizations are built upon the first-order Euler and second-order BDF method, respectively. We derive the unconditional energy stability for both schemes and also establish the rigorous error estimates for the first-order SAV Fourier-spectral scheme. Finally, various numerical experiments are presented to demonstrate the accuracy and performance for the constructed schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wise, S.M.: Unconditionally stable finite difference, nonlinear multigrid simulation of the Cahn-Hilliard-Hele-Shaw system of equations. J. Sci. Comput. 44 (1), 38–68 (2010)

    Article  MathSciNet  Google Scholar 

  2. Han, D., Wang, X.: Decoupled energy-law preserving numerical schemes for the Cahn-Hilliard-Darcy system. Numer. Methods Partial Differ. Equat. 32(3), 936–954 (2016)

    Article  MathSciNet  Google Scholar 

  3. Han, D., Wang, X.: A second order in time, decoupled, unconditionally stable numerical scheme for the Cahn-Hilliard-Darcy system. J. Sci. Comput. 77(2), 1210–1233 (2018)

    Article  MathSciNet  Google Scholar 

  4. Feng, X., Prohl, A.: Numerical analysis of the Cahn-Hilliard equation and approximation for the Hele-Shaw problem. Interfaces Free Boundaries 7(1), 1–28 (2005)

    Article  MathSciNet  Google Scholar 

  5. Wang, X., Zhang, Z.: Well-posedness of the Hele-Shaw-Cahn-Hilliard system. Ann. l’IHP Anal. Linéaire 30(3), 367–384 (2013)

    MathSciNet  MATH  Google Scholar 

  6. Feng, X., Wise, S.: Analysis of a Darcy-Cahn-Hilliard diffuse interface model for the Hele-Shaw flow and its fully discrete finite element approximation. SIAM J. Numer. Anal. 50(3), 1320–1343 (2012)

    Article  MathSciNet  Google Scholar 

  7. Gao, Y., Li, R., Mei, L., Lin, Y.: A second-order decoupled energy stable numerical scheme for Cahn-Hilliard-Hele-Shaw system. Appl. Numer. Math. 157, 338–355 (2020)

    Article  MathSciNet  Google Scholar 

  8. Liu, C., Shen, J.: A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Physica D Nonlinear Phenom. 179(3-4), 211–228 (2003)

    Article  MathSciNet  Google Scholar 

  9. Li, Y., Yu, Q., Fang, W., Xia, B., Kim, J.: A stable second-order BDF scheme for the three-dimensional Cahn-Hilliard-Hele-Shaw system. Adv. Comput. Math. 47(1), 1–18 (2021)

    Article  MathSciNet  Google Scholar 

  10. Chen, W., Liu, Y., Wang, C., Wise, S.: Convergence analysis of a fully discrete finite difference scheme for the Cahn-Hilliard-Hele-Shaw equation. Math. Comput. 85(301), 2231–2257 (2016)

    Article  MathSciNet  Google Scholar 

  11. Shen, J., Xu, J., Yang, J.: The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 353, 407–416 (2018)

    Article  MathSciNet  Google Scholar 

  12. Shen, J.: Efficient and accurate structure preserving schemes for complex nonlinear systems. In: Handbook of Numerical Analysis, vol. 20, pp 647–669. Elsevier (2019)

  13. Liu, Z., Li, X.: The exponential scalar auxiliary variable (E-SAV) approach for phase field models and its explicit computing. SIAM J. Sci. Comput. 42(3), B630–B655 (2020)

    Article  MathSciNet  Google Scholar 

  14. Zhuang, Q., Shen, J.: Efficient, SAV approach for imaginary time gradient flows with applications to one-and multi-component Bose-Einstein Condensates. J. Comput. Phys. 396, 72–88 (2019)

    Article  MathSciNet  Google Scholar 

  15. Li, X., Shen, J., Rui, H.: Energy stability and convergence of SAV block-centered finite difference method for gradient flows. Math. Comput. 88(319), 2047–2068 (2019)

    Article  MathSciNet  Google Scholar 

  16. Li, X., Shen, J.: On a SAV-MAC scheme for the Cahn-Hilliard-Navier-Stokes phase-field model and its error analysis for the corresponding Cahn-Hilliard-Stokes case. Math. Models Methods Appl. Sci. pp. 1–35 (2020)

  17. Shen, J., Tang, T., Wang, L.-L.: Spectral methods: algorithms, analysis and applications, vol. 41. Springer Science & Business Media, New York (2011)

    Book  Google Scholar 

  18. Li, X., Shen, J.: Stability and error estimates of the SAV Fourier-spectral method for the phase field crystal equation. Adv. Comput. Math. 46 (3), 48 (2020)

    Article  MathSciNet  Google Scholar 

  19. Weng, Z., Zhai, S., Feng, X.: A Fourier spectral method for fractional-in-space Cahn-Hilliard equation. Appl. Math. Model. 42, 462–477 (2017)

    Article  MathSciNet  Google Scholar 

  20. Shen, J., Xu, J.: Convergence and error analysis for the scalar auxiliary variable (SAV) schemes to gradient flows. SIAM J. Numer. Anal. 56(5), 2895–2912 (2018)

    Article  MathSciNet  Google Scholar 

  21. Li, X., Shen, J.: On fully decoupled MSAV schemes for the Cahn-Hilliard-Navier-Stokes model of Two-Phase Incompressible Flows. arXiv:2009.09353

  22. Guo, R., Xia, Y., Xu, Y.: An efficient fully-discrete local discontinuous galerkin method for the Cahn-Hilliard-Hele-Shaw system. J. Comput. Phys. 264, 23–40 (2014)

    Article  MathSciNet  Google Scholar 

  23. Han, D.: A decoupled unconditionally stable numerical scheme for the Cahn-Hilliard-Hele-Shaw system. J. Sci. Comput. 66(3), 1102–1121 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China under grant numbers 11901489 and 12131014.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences and Fujian Provincial Key Laboratory on Mathematical Modeling and High Performance Scientific Computing, Xiamen University, 361005, Xiamen, Fujian, China

    Nan Zheng

  2. School of Mathematics, Shandong University, 250100, Jinan, Shandong, People’s Republic of China

    Xiaoli Li

Authors
  1. Nan Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoli Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaoli Li.

Additional information

Communicated by: Silas Alben

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, N., Li, X. Error analysis of the SAV Fourier-spectral method for the Cahn-Hilliard-Hele-Shaw system. Adv Comput Math 47, 71 (2021). https://doi.org/10.1007/s10444-021-09897-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-021-09897-0

Keywords

Mathematics Subject Classification (2010)

Search

Navigation