Abstract
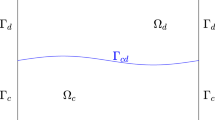
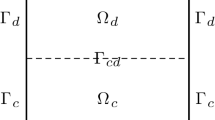
The recently developed dual-porosity-Stokes model describes a complicated dual-porosity-conduit system which uses a dual-porosity/permeability model to govern the flow in porous media coupled with free flow via four physical interface conditions. This system has important applications in unconventional reservoirs especially the multistage fractured horizontal wellbore problems. In this paper, we propose and analyze domain decomposition methods to decouple the large system arisen from the discretization of dual-porosity-Stokes model. Robin boundary conditions are used to decouple the coupling conditions on the interface. Then, Robin-Robin domain decomposition methods are constructed based on the two decoupled sub-problems. Convergence analysis is demonstrated and a geometric convergence order is obtained. Optimized Schwarz methods are proposed for the dual-porosity-Stokes model and optimized Robin parameters are obtained to improve the convergence of proposed algorithms. Three computational experiments are presented to illustrate and validate the accuracy and applicability of proposed algorithms.
Similar content being viewed by others
References
Ervin, V.J., Jenkins, E.W., Sun, S.: Coupled generalized nonlinear Stokes flow with flow through a porous medium. SIAM J. Numer Anal. 47(2), 929–952 (2009)
Fraunhofer, W., Winter, G.: The use of asymmetrical flow field-flow fractionation in pharmaceutics and biopharmaceutics. Eur. J. Pharm. Biopharm. 58 (2), 369–383 (2004)
Cao, S., Pollastrini, J., Jiang, Y.: Separation and characterization of protein aggregates and particles by field flow fractionation. Curr. Pharm. Biotechnol. 10(4), 382–390 (2009)
D’Angelo, C., Zunino, P.: Robust numerical approximation of coupled Stokes’ and Darcy’s flows applied to vascular hemodynamics and biochemical transport. ESAIM Math. Model. Numer. Anal. 45(3), 447–476 (2011)
Chen, J., Sun, S., Wang, X.: A numerical method for a model of two-phase flow in a coupled free flow and porous media system. J. Comput. Phys. 268, 1–16 (2014)
Arbogast, T., Gomez, M.: A discretization and multigrid solver for a Darcy-Stokes system of three dimensional vuggy porous media. Comput. Geosci. 13(3), 331–348 (2009)
Nassehi, V.: Modelling of combined Navier-Stokes and Darcy flows in crossflow membrane filtration. Chem. Eng. Sci. 53, 1253–1265 (1998)
Hanspal, N., Waghode, A., Nassehi, V., Wakeman, R.: Numerical analysis of coupled Stokes/Darcy flow in industrial filtrations. Transp. Porous Media 64, 73–101 (2006)
Hoppe, R., Porta, P., Vassilevski, Y.: Computational issues related to iterative coupling of subsurface and channel flows. Calcolo 44(1), 1–20 (2007)
Discacciati, M., Miglio, E., Quarteroni, A.: Mathematical and numerical models for coupling surface and groundwater flows. Appl. Numer. Math. 43(1–2), 57–74 (2002)
Çeşmelioğlu, A., Rivière, B.: Primal discontinuous Galerkin methods for time-dependent coupled surface and subsurface flow. J. Sci. Comput. 40(1–3), 115–140 (2009)
Babuška, I., Gatica, G.N.: A residual-based a posteriori error estimator for the Stokes-Darcy coupled problem. SIAM J. Numer. Anal. 48(2), 498–523 (2010)
Gatica, G.N., Oyarzúa, R., Sayas, F.J.: A residual-based a posteriori error estimator for a fully-mixed formulation of the Stokes-Darcy coupled problem. Comput. Methods Appl. Mech. Eng. 200(21–22), 1877–1891 (2011)
Boubendir, Y., Tlupova, S.: Domain decomposition methods for solving Stokes-Darcy problems with boundary integrals. SIAM J. Sci. Comput. 35(1), B82–B106 (2013)
Wang, W., Xu, C.: Spectral methods based on new formulations for coupled Stokes and Darcy equations. J. Comput. Phys. 257(part A), 126–142 (2014)
Vassilev, D., Yotov, I.: Coupling Stokes-Darcy with flow transport. SIAM J. Sci. Comput. 31(5), 3661–3684 (2009)
Tlupova, S., Cortez, R.: Boundary integral solutions of coupled Stokes and Darcy flows. J. Comput. Phys. 228(1), 158–179 (2009)
Rybak, I., Magiera, J.: A multiple-time-step technique for coupled free flow and porous medium systems. J. Comput. Phys. 272(272), 327–342 (2014)
Rivière, B., Yotov, I.: Locally conservative coupling of Stokes and Darcy flows. SIAM J. Numer. Anal. 42(5), 1959–1977 (2005)
Münzenmaier, S., Starke, G.: First-order system least squares for coupled Stokes-Darcy flow. SIAM J. Numer. Anal. 49(1), 387–404 (2011)
Mu, M., Zhu, X.: Decoupled schemes for a non-stationary mixed Stokes-Darcy model. Math. Comput. 79(270), 707–731 (2010)
Mu, M., Xu, J.: A two-grid method of a mixed Stokes-Darcy model for coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 45 (5), 1801–1813 (2007)
Márquez, A., Meddahi, S., Sayas, F.J.: A decoupled preconditioning technique for a mixed Stokes-Darcy model. J. Sci. Comput. 57(1), 174–192 (2013)
Layton, W.J., Schieweck, F., Yotov, I.: Coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 40(6), 2195–2218 (2002)
Girault, V., Vassilev, D., Yotov, I.: Mortar multiscale finite element methods for Stokes-Darcy flows. Numer. Math. 127(1), 93–165 (2014)
Girault, V., Rivière, B.: DG approximation of coupled Navier-Stokes and Darcy equations by Beaver-Joseph-Saffman interface condition. SIAM J. Numer. Anal. 47(3), 2052–2089 (2009)
Galvis, J., Sarkis, M.: FETI and BDD preconditioners for Stokes-Mortar-Darcy systems. Commun. Appl. Math. Comput. Sci. 5, 1–30 (2010)
Ervin, V.J., Jenkins, E.W., Lee, H.: Approximation of the Stokes-Darcy system by optimization. J. Sci. Comput. 59(3), 775–794 (2014)
Discacciati, M., Quarteroni, A., Valli, A.: Robin-Robin domain decomposition methods for the Stokes-Darcy coupling. SIAM J. Numer Anal. 45(3), 1246–1268 (2007)
Chen, W., Gunzburger, M., Hua, F., Wang, X.: A parallel Robin-Robin domain decomposition method for the Stokes-Darcy system. SIAM J. Numer. Anal. 49(3), 1064–1084 (2011)
Cao, Y., Gunzburger, M., Hu, X., Hua, F., Wang, X., Zhao, W.: Finite element approximation for Stokes-Darcy flow with Beavers-Joseph interface conditions. SIAM J. Numer. Anal. 47(6), 4239–4256 (2010)
Badea, L., Discacciati, M., Quarteroni, A.: Numerical analysis of the Navier-Stokes/Darcy coupling. Numer. Math. 115(2), 195–227 (2010)
Hou, J., Qiu, M., He, X., Guo, C., Wei, M., Bai, B.: A dual-porosity-stokes model and finite element method for coupling dual-porosity flow and free flow. SIAM J. Sci. Comput. 38(5), B710–B739 (2016)
Chen, W., Gunzburger, M., Sun, D., Wang, X.: An efficient and long-time accurate third-order algorithm for the Stokes-Darcy system. Numer. Math. 134(4), 857–879 (2016)
Layton, W., Tran, H., Trenchea, C.: Analysis of long time stability and errors of two partitioned methods for uncoupling evolutionary groundwater-surface water flows. SIAM J. Numer. Anal. 51(1), 248–272 (2013)
Rivière, B.: Analysis of a discontinuous finite element method for the coupled Stokes and Darcy problems. J. Sci. Comput. 22(/23), 479–500 (2005)
Kanschat, G., Riviére, B.: A strongly conservative finite element method for the coupling of Stokes and Darcy flow. J. Comput. Phys. 229, 5933–5943 (2010)
Chidyagwai, P., Rivière, B.: On the solution of the coupled Navier-Stokes and Darcy equations. Comput. Methods Appl. Mech. Eng. 198(47–48), 3806–3820 (2009)
Urquiza, J.M., N’Dri, D., Garon, A., Delfour, M.C.: Coupling Stokes and Darcy equations. Appl. Numer. Math. 58(5), 525–538 (2008)
Rui, H., Zhang, R.: A unified stabilized mixed finite element method for coupling Stokes and Darcy flows. Comput. Methods Appl. Mech. Eng. 198(33–36), 2692–2699 (2009)
Karper, T., Mardal, K.A., Winther, R.: Unified finite element discretizations of coupled Darcy-Stokes flow. Numer. Methods Partial Differ. Equ. 25 (2), 311–326 (2009)
Feng, M., Qi, R., Zhu, R., Ju, B.: Stabilized Crouzeix-Raviart element for the coupled Stokes and Darcy problem. Appl. Math. Mech. (English Ed.) 31(3), 393–404 (2010)
Chen, W., Chen, P., Gunzburger, M., Yan, N.: Superconvergence analysis of FEMs for the Stokes-Darcy system. Math Methods Appl. Sci. 33(13), 1605–1617 (2010)
Çeşmelioğlu, A., Rivière, B.: Analysis of time-dependent Navier-Stokes flow coupled with Darcy flow. J. Numer. Math. 16(4), 249–280 (2008)
Arbogast, T., Brunson, D.S.: A computational method for approximating a Darcy-Stokes system governing a vuggy porous medium. Comput. Geosci. 11(3), 207–218 (2007)
He, X.-M., Li, J., Lin, Y., Ming, J.: A domain decomposition method for the steady-state Navier-Stokes-Darcy model with Beavers-Joseph interface condition. SIAM J. Sci. Comput. 37(5), S264–S290 (2015)
Shan, L., Zheng, H.: Partitioned time stepping method for fully evolutionary Stokes-Darcy flow with Beavers-Joseph interface conditions. SIAM J. Numer. Anal. 51(2), 813–839 (2013)
Shan, L., Zheng, H., Layton, W.: A decoupling method with different sub-domain time steps for the nonstationary Stokes-Darcy model. Numer. Methods Partial Differ. Equ. 29(2), 549–583 (2013)
Galvis, J., Sarkis, M.: Balancing domain decomposition methods for mortar coupling Stokes-Darcy systems. In: Domain Decomposition Methods in Science and Engineering XVI. Lect. Notes Comput. Sci. Eng., vol. 55, pp. 373–380. Springer, Berlin (2007)
Boubendir, Y., Tlupova, S.: Stokes-Darcy boundary integral solutions using preconditioners. J. Comput. Phys. 228(23), 8627–8641 (2009)
Bernardi, C., Rebollo, T.C., Hecht, F., Mghazli, Z.: Mortar finite element discretization of a model coupling Darcy and Stokes equations. M2AN Math. Model. Numer. Anal. 42(3), 375–410 (2008)
Gatica, G.N., Meddahi, S., Oyarzúa, R.: A conforming mixed finite-element method for the coupling of fluid flow with porous media flow. IMA J. Numer. Anal. 29(1), 86–108 (2009)
Jiang, B.: A parallel domain decomposition method for coupling of surface and groundwater flows. Comput. Methods Appl. Mech. Eng. 198(9–12), 947–957 (2009)
Discacciati, M., Quarteroni, A.: Analysis of a domain decomposition method for the coupling of Stokes and Darcy equations. In: Numerical Mathematics and Advanced Applications, pp. 3–20. Springer Italia, Milan (2003)
Discacciati, M., Quarteroni, A.: Convergence analysis of a subdomain iterative method for the finite element approximation of the coupling of Stokes and Darcy equations. Comput. Vis. Sci. 6(2–3), 93–103 (2004)
Discacciati, M.: Domain decomposition methods for the coupling of surface and groundwater flows. PhD thesis, Ecole Polytechnique Fédérale de Lausanne, Switzerland (2004)
Cao, Y., Gunzburger, M., He, X.-M., Wang, X.: Parallel, non-iterative, multi-physics domain decomposition methods for time-dependent Stokes-Darcy systems. Math. Comput. 83(288), 1617–1644 (2014)
Cao, Y., Gunzburger, M., He, X.-M., Wang, X.: Robin-Robin domain decomposition methods for the steady Stokes-Darcy model with Beaver-Joseph interface condition. Numer. Math. 117(4), 601–629 (2011)
Cai, M., Mu, M., Xu, J.: Preconditioning techniques for a mixed Stokes/Darcy model in porous media applications. J. Comput. Appl. Math. 233(2), 346–355 (2009)
Shan, L., Hou, J., Yan, W., Chen, J.: Partitioned time stepping method for a dual-porosity-Stokes model. J. Sci. Comput. 79(1), 389–413 (2019)
Arbogast, T.: The existence of weak solutions to single porosity and simple dual-porosity models of two-phase incompressible flow. Nonlinear Anal. 19(11), 1009–1031 (1992)
Douglas, J., Kischinhevsky, M., Paes Leme, P.J., Spagnuolo, A.M.: A multiple-porosity model for a single-phase flow through naturally-fractured porous media. Comput. Appl. Math. 17(1), 19–48 (1998)
Barenblatt, G.E., Zheltov, I.P., Kochina, I.N.: Basic concepts in the theory of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 24, 1286–1303 (1960)
Warren, J.E., Root, P.J.: The behavior of naturally fractured reservoirs. Soc. Petrol. Eng. J. 3(3), 245–255 (1963)
Austria, J.J.C., O’Sullivan, M.J.: Dual porosity models of a two-phase geothermal reservoir. In: Proceedings World Geothermal Congress. Melbourne (2015)
Aguilera, R: Naturally fractured reservoirs. In: Proceedings World Geothermal Congress. Pennwell Publishing Company, Tulsa (1995)
Discacciati, M., Gerardo-Giorda, L.: Optimized Schwarz methods for the Stokes-Darcy coupling. IMA J. Numer. Anal. 38(4), 1959–1983 (2018)
Gander, M.J., Vanzan, T.: On the derivation of optimized transmission conditions for the stokes-darcy coupling. In: Domain Decomposition Methods in Science and Engineering XXV. LNCSE. Springer (2019)
Saffman, P.: On the boundary condition at the interface of a porous medium. Stud. Appl. Math. 1, 77–84 (1971)
Toselli, A., Widlund, O B: Domain Decomposition Methods—Algorithms and Theory. Springer, New York (2004)
Lions, P.-L.: On the Schwarz alternating method. III. A variant for nonoverlapping subdomains. In: Third International Symposium on Domain Decomposition Methods for Partial Differential Equations (Houston, TX, 1989), pp. 202–223. SIAM, Philadelphia (1990)
Gander, M.J.: Optimized Schwarz methods. SIAM J. Numer. Anal. 44(4), 699–731 (2006)
Brenner, S. C., Scott, L R: The Mathematical Theory of Finite Element Methods. Springer, New York (1994)
Smolen, J.J.: Cased Hole and Production Log Evaluation. PennWell Books (1996)
Seale, R. A., Donaldson, J., Athans, J.: Multistage fracturing system: improving operational efficiency and production. In: SPE Eastern Regional Meeting. Society of Petroleum Engineers (2006)
Bello, R.O., Wattenbarger, R.A.: Multi-stage hydraulically fractured shale gas rate transient analysis. In: Paper SPE 126754 Presented at the SPE North Africa Technical Conference and Exhibition held in Cairo, pp. 14–17, Egypt (2010)
Gigante, G., Pozzoli, M., Vergara, C.: Optimized Schwarz Methods for the diffusion-reaction problem with cylindrical interfaces. SIAM J. Numer. Anal. 51(6), 3402–3420 (2013)
Funding
This work is partially supported by NSFC (Grant Nos. 11701451, 11971377, 11931013, and 12001421), NSF of Shaanxi Province (Nos. 2019JM-367 and 2018JQ1077), and Scientific Research Program funded by Shaanxi Provincial Education Department (20JK0782).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by: Francesca Rapetti
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 3.3
Adding (3.29) and (3.30), summing over k from k = 1 to N, then we can obtain:
By the coercivity of the bilinear forms on the right-hand side of (5.1), we have:
where C0 is given in (2.22). Hence, \(\left \|{\mathbf {e}}_{u}^{k}\right \|_{1}\), \(\left \|{e_{m}^{k}}\right \|_{1}\), and \(\left \|{e_{f}^{k}}\right \|_{1}\) tend to zero, respectively. Passing k to the limit in the error (3.16) will result in:
which implies the convergence of \({\varepsilon _{d}^{k}}\) in \(H^{-\frac 12}({\Gamma }_{cd})\). Through the convergence of \({\varepsilon ^{k}_{d}}\) and \({e_{f}^{k}}\) together with the error (3.19), we deduce the convergence of \({\varepsilon _{c}^{k}}\) in \(H^{-\frac 12}({\Gamma }_{cd})\). The convergence of the pressure \({e_{p}^{k}}\) follows from the inf-sup condition (2.21) and (3.17). Then, the theorem is obtained. □
Proof of Theorem 3.4
It is easy to show the following coercivity properties:
where the constants C1 and C2, also the constants C3, C4, and C5 used below, are given in (2.13)–(2.16). Since (3.31) and (3.32) are satisfied, then from (5.4) and (5.5) and trace inequalities (2.15) and (2.16), we deduce:
and
where \(\left \|{\mathbf {e}}_{u}^{k}\cdot \mathbf {n}_{cd}\right \|_{L^{2}({\Gamma }_{cd})}\) is bounded from above by \(\left \|{\mathbf {e}}_{u}^{k}\right \|_{L^{2}({\Gamma }_{cd})}\) and then by (2.16). Plugging (5.6) and (5.7) into (3.21) and (3.22), respectively, we can obtain:
Above recurrence formula implies the geometric convergence rate \(\sqrt { \gamma _{c}/\gamma _{d}}\) for \({\varepsilon _{c}^{k}}\) and \({\varepsilon _{d}^{k}}\), as follows:
Above two inequalities are true whether k is even or odd. For the sake of simplification, define:
Next, we derive the convergence rate for \({e_{m}^{k}}\), \({e_{f}^{k}}\), \({\mathbf {e}}_{u}^{k}\) and \({e_{p}^{k}}\) via the error equations (3.16)–(3.18) and (5.11). Setting \(\psi _{m}={e_{m}^{k}} \) and \(\psi _{f}={e_{f}^{k}} \) in (3.16), we have:
By (5.12), Poincaré inequality (2.13), Cauchy-Schwarz inequality, and trace inequality (2.15), we deduce
where the middle inequality follows from (5.12). Substituting the first estimate in (5.11) into (5.13), then we can obtain the convergence rate of \({p^{k}_{f}}\):
Using (5.11), (5.14), and (5.15), we can obtain the convergence rate of \({p^{k}_{m}}\):
From (3.17) and the trace inequality (2.16), we have:
and the convergence rate of uk is
Furthermore, rewriting (3.17) and estimating the upper bound of the bilinear form bS(⋅,⋅), as follows:
for all v ∈V0. Due to the inf-sup condition (2.21) combined with the upper bound (5.19), we deduce:
Hence, we have proved the convergence theorem for Case 2. □
Rights and permissions
About this article
Cite this article
Hou, J., Yan, W., Hu, D. et al. Robin-Robin domain decomposition methods for the dual-porosity-conduit system. Adv Comput Math 47, 7 (2021). https://doi.org/10.1007/s10444-020-09828-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10444-020-09828-5