Abstract
In medicine, confounding variables in a generalized linear model are often adjusted; however, these variables have not yet been exploited in a non-linear deep learning model. Sex plays important role in bone age estimation, and non-linear deep learning model reported their performances comparable to human experts. Therefore, we investigate the properties of using confounding variables in a non-linear deep learning model for bone age estimation in pediatric hand X-rays. The RSNA Pediatric Bone Age Challenge (2017) dataset is used to train deep learning models. The RSNA test dataset is used for internal validation, and 227 pediatric hand X-ray images with bone age, chronological age, and sex information from Asan Medical Center (AMC) for external validation. U-Net based autoencoder, U-Net multi-task learning (MTL), and auxiliary-accelerated MTL (AA-MTL) models are chosen. Bone age estimations adjusted by input, output prediction, and without adjusting the confounding variables are compared. Additionally, ablation studies for model size, auxiliary task hierarchy, and multiple tasks are conducted. Correlation and Bland–Altman plots between ground truth and model-predicted bone ages are evaluated. Averaged saliency maps based on image registration are superimposed on representative images according to puberty stage. In the RSNA test dataset, adjusting by input shows the best performances regardless of model size, with mean average errors (MAEs) of 5.740, 5.478, and 5.434 months for the U-Net backbone, U-Net MTL, and AA-MTL models, respectively. However, in the AMC dataset, the AA-MTL model that adjusts the confounding variable by prediction shows the best performance with an MAE of 8.190 months, whereas the other models show the best performances by adjusting the confounding variables by input. Ablation studies of task hierarchy reveal no significant differences in the results of the RSNA dataset. However, predicting the confounding variable in the second encoder layer and estimating bone age in the bottleneck layer shows the best performance in the AMC dataset. Ablations studies of multiple tasks reveal that leveraging confounding variables plays an important role regardless of multiple tasks. To estimate bone age in pediatric X-rays, the clinical setting and balance between model size, task hierarchy, and confounding adjustment method play important roles in performance and generalizability; therefore, proper adjusting methods of confounding variables to train deep learning-based models are required for improved models.
Supplementary Information
The online version contains supplementary material available at 10.1007/s10278-023-00849-2.
Keywords: Bone age estimation; Confounding variable; Deep learning; Model enhancement; Multi-task learning, Pediatric X-ray
Introduction
With recent advancements in computational resources, deep learning has performed well in several areas. Adding additional non-linearities and layers has improved the performances of deep learning models [1]. It has enabled tasks that were difficult or impossible for linear models before, such as the XOR problem or image analyses. Numerous deep learning models showed decent performances in the ImageNet Large Scale Visual Recognition Challenge [2, 3]. Moreover, they can analyze medical images, and recent studies have shown that important medical variables, such as biological age [4] and sex [5], can be predicted. Moreover, recent advances in medical image analysis techniques that employ deep learning has reported their performances comparable to human experts and their effectiveness in clinical applications [6, 7].
In statistical analyses using generalized linear models, such as linear regression, logistic regression, and Poisson regression [8], adjusting confounding variables is a common and critical procedure [9, 10], particularly in medicine [11, 12]. Particularly, age and sex are major confounding variables and therefore frequently adjusted [13–16]. However, the method of handling these important confounding variables in a deep learning model has been insufficiently investigated.
Biological age estimation using skeletal images is important in pediatric endocrinology and genetics. For example, adult height can be predicted through skeletal age [17, 18], and the discrepancy between the chronological age and bone age of children can indicate pathological genetic [19], endocrine [20, 21], and systemic conditions [22–25]. Recently, numerous deep learning-based approaches for automatically estimating bone age from pediatric hand X-rays have been made [26]. One article noted that sex and age itself can affect the generalizability and bias of bone age estimation model [27]. The challenge-winning models leveraged sex information by using additional encoders for sex or additional dense layers [26]. However, most studies only considered this important confounding variable as input variable.
Although non-linearity has allowed deep learning to show decent performances, confounding variables and linear models play an important role in medicine. In pediatric bone age estimation, sex information and laboratory results (e.g., growth hormone, estrogen, and testosterone) are such important variables [28]. Herein, we presented the differences in performance and generalizability according to different handling strategies of confounding variables in non-linear deep learning models for bone age estimation in pediatric hand X-rays. The main contributions of our study are as follows:
We experimented with and compared different methods for handling sex information in deep learning model for bone age estimation.
We proposed the role of hierarchical multi-task learning architecture as a confounding variable handling architecture.
We suggested auxiliary-accelerated multi-task learning architecture to better utilize confounding variables to improve the performance and robustness of models.
Materials and Methods
This retrospective study was conducted according to the principles of the Declaration of Helsinki and according to current scientific guidelines. The study protocol was approved by the Institutional Review Board (IRB) Committee. The requirement for informed patient consent was waived by the IRB.
Dataset and Preprocessing
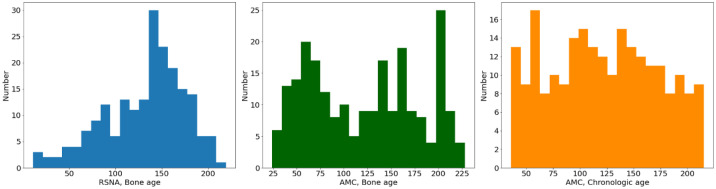
A large dataset for skeletal age prediction consisting of hand X-ray images with bone age and sex information has been released by the Radiological Society of North America (RSNA) [26, 29]. The RSNA dataset is composed of 12,611 training images, 1,425 validation images, and 200 testing images. To train the bone age prediction model, only the RSNA dataset was used. For this dataset, the Greulich and Pyle [30] (GP) method, which interprets bone age by comparing hand X-rays with representative images, was used to measure the ground truth bone age. For external validation, 227 hand X-rays of clinically normal participants with sex information from the South Korean referral hospital, Asan Medical Center (AMC), were used. For the AMC dataset, two expert radiologists labeled the bone ages using the GP method. The mean of the bone age label and chronological age was used for evaluation. The bone ages of the RSNA test dataset were similarly distributed to those in the train dataset; the study populations were sampled according to the uniform distribution of chronological age in the AMC dataset. These two datasets showed significantly different distributions according to two-sample Kolmogorov–Smirnov test for goodness of fit (P-value < 0.001). The bone ages of participants ranged from 11 to 219 months in the RSNA dataset, while they ranged from 24 to 228 in the AMC dataset. The age histograms of the RSNA and AMC datasets are depicted in Fig. 1.
Fig. 1.
Age histograms of each age label. RSNA, Radiological Society of North America; AMC, Asan Medical Center
When preprocessing the images, they were first adjusted from the top 1% pixel value to avoid L/R markers and other high intensity artifacts acting as confounding factors [31]. To preserve the original image shape, the images were padded into a square. And they were reshaped into 512 × 512 pixels, considering the sophisticated nature of medical images and resource limitations, such as training time and GPU memory. The pixel values were normalized from 0 to 1 using min–max scaling; Additionally, contrast limited adaptive histogram equalization was used to emphasize the bony part of hand X-rays.
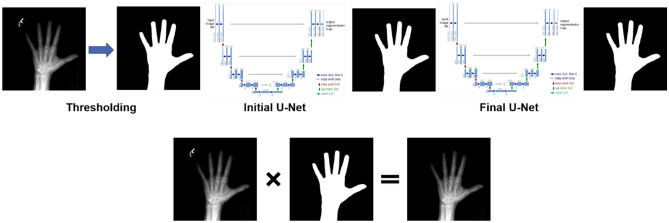
U-Net [32] was trained for hand-image segmentation using a semi-automated data labeling strategy. 200 randomly sampled hand X-ray images were binarized and small clusters were removed. The first U-Net segmentation network was trained using these masks and the intersection over union (IoU) for the baseline 200 images was 0.982. Subsequently, additional masks were generated from this network using the training dataset. Next, well-generated masks were sampled and the U-Net segmentation network was trained with these masks. The final IoU for the entire RSNA dataset was 0.975. Finally, a hand mask was generated for all training, validation, and testing datasets. Hand images only were extracted and used for bone age prediction. The hand mask generation and hand extraction processes are summarized in Fig. 2.
Fig. 2.
Hand mask generation and hand extraction using U-Net
Network Architectures
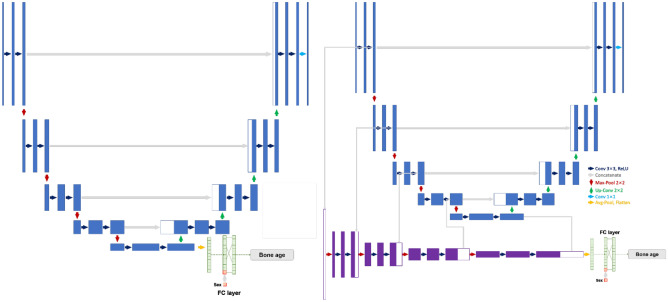
U-Net based multi-task learning (MTL) architecture was adopted for bone age estimation. The network simultaneously conducted bone age estimation and image reconstruction tasks; therefore, the model could learn good representations when reconstructing the original image from the augmented image. An auxiliary regression layer was added to the bottleneck layer of the U-Net architecture to estimate bone age. Furthermore, because bone age estimation was the main target for the entire architecture, additional encoder layers were added to accelerate the target auxiliary regression task. The schematic figure of U-Net MTL and auxiliary-accelerated MTL (AA-MTL) architecture is depicted in Fig. 3.
Fig. 3.
U-Net based multi-task learning (MTL) architecture, which simultaneously conducts image reconstruction and bone age estimation. Figure on the left depicts U-Net MTL architecture and the right depicts the auxiliary-accelerated (AA) MTL architecture. Additional encoders are added in the AA-MTL model to accelerate the target auxiliary regression task. In this figure, sex information is handled as an input vector, which is concatenated before the fully connected layer for bone age estimation
Handling Methods of Confounding Variables
In the typical statistical model (i.e., generalized linear models), the relationship between the observation Yi and independent variable Xij is formulated as a linear combination of independent variables and parameters as:
| 1 |
given a random sample (Yi, Xi1, Xi2, …, Xij-1, Xij), where W1, W2, …, Wj-1, Wj are the parameters for the variables Xi1, Xi2, …, Xij-1, Xij; and βi is the random bias.
However, considering the non-linear properties of deep learning, the relationship between the input vector vij and output vector uij cannot be defined as in Eq. (1). The relationship between vectors vij and uij in a non-linear deep learning model can be formulated as:
| 2 |
Therefore, three different handling methods of the important confounding variable (sex) in non-linear deep learning models were compared. The model that did not use sex information was regarded as the baseline. The models that used sex information as the input vector and predicted sex information as the output vector were trained. When sex was set as an input to a deep learning model, sex was concatenated just before the fully connected layer for bone age estimation; when sex was set as an output, an auxiliary classifier was added to predict it.
Furthermore, the backpropagation from one loss function was hypothesized to affect another loss function, and vice versa. Therefore, sex classification and bone age estimation at the diverse encoder level were investigated when sex was set as the prediction output. The hierarchical model structures of the following were compared. Bone age estimation after bottleneck block, followed by sex classification after second encoder block (the two-convolutional layer followed by the max pooling layer or input image was considered as an encoder block, see Fig. 3); sex classification after bottleneck block, followed by bone age estimation after second encoder block; and sex classification and bone age estimation simultaneously after bottleneck block.
Average Class Activation Maps
Saliency maps using gradient-weighted class activation map (Grad-CAM) [33] were acquired to assess the explainability of each model. The Grad-CAM images were stratified by pubertal stage because the growth patterns of children change with the pubertal stage. Therefore, the hand X-ray images were grouped into pre-puberty (0–6 years), puberty (6–14 for boys, 6–12 for girls), and post-puberty (14–18 for boys, 12–18 for girls) [34–36].
Next, the image registration technique was applied to the pubertal stage-stratified Grad-CAMs to show each model focus on. First, the representative image of each pubertal stage was selected. The center, width, and height from the hand mask of each image was acquired. Subsequently, an affine transformation using the center, width, and height of the hand mask was applied to the Grad-CAM and averaged. Finally, the averaged Grad-CAM was superimposed on the representative image of each pubertal stage.
Statistical Analyses
Parametric and nonparametric statistics were used on the RSNA and AMC datasets, respectively, as the RSNA dataset was similarly distributed to the train dataset, while the AMC dataset was not. The mean average error (MAE) and Pearson’s correlation coefficient (r) or the Kendall rank correlation coefficient (τ) between the model-estimated bone age and ground truth age were evaluated and compared. A paired t-test and Wilcoxon signed-rank test were conducted on the RSNA and AMC datasets, respectively, to compare the statistical differences between each model. Correlation plots and Bland–Altman plots [37, 38] were constructed to show the correlation between the estimated bone age and ground truth age. The statistics software R version 4.2.0 (R Foundation for Statistical Computing, Vienna, Austria) was used for all statistical analyses. Two-sided P-values were used to determine statistical significance, which was set at an alpha value of 0.05.
Experiments
Implementation Details
U-Net [32] based encoder-decoder architecture was adopted. Because deep learning models can learn good representations from self-reconstruction of the original image [39], the U-Net decoder learnt to reconstruct the original image from the augmented image. The models without decoders were trained to isolate the effect of this self-reconstruction. All models were implemented in Python version 3.6.9 with PyTorch version 1.9.0. Adam optimizer was chosen with a learning rate of 5e-3, and the ReduceLROnPlateau learning rate scheduler was used. The models were trained with augmentation techniques plausible for medical images, such as shifting, zooming, rotation, blur, gaussian noise addition, and sharpening. Additionally, strong augmentation, such as cutout [40], was used to the extent that it did not compromise clinical viability. All networks were trained using a single GPU (Titan RTX) and a batch size of eight. For bone age estimation, regression loss was calculated as L1 Loss, as was image reconstruction loss. L1 loss was calculated as:
| 3 |
where y is ground truth age and is bone age regression output when applied as regression loss. When applied as reconstruction loss, y was regarded as the original image and as the model reconstruction output. When sex was set as the prediction output, the classification loss was calculated using cross entropy loss:
| 4 |
where is the softmax probability of the model classification output. As the target task was bone age estimation and the other tasks were performed for confounding adjustment, the loss weights for the image reconstruction and sex classification were set to 0.1 and the sum of loss weights was set to 1 (i.e., bone age estimation weight + image reconstruction weight, if performed + sex classification weight, if performed = 1). The models were trained from the scratch without pretrained weights.
Comparison of Handling Methods of Confounding Variables
A comparison of the confounding handling methods in U-Net backbone, U-Net MTL, and AA-MTL is summarized in Table 1. The absolute errors between the model-predicted bone age and ground truth age label were compared for each confounding adjustment method and the best performing method for each architecture. The correlation analyses between the model-predicted bone age and ground truth age labels are depicted in Supplementary Table 1.
Table 1.
Comparison of confounding adjustment methods in RSNA and AMC datasets with each architecture
| Architecture (Parameters) | Confounding adjustment | RSNA dataset | AMC dataset | |
|---|---|---|---|---|
| MAE (BA)a | MAE (BA)b | MAE (CA)b | ||
| U-Net backbone (14.13 M) | No | 7.966 ± 6.693*** | 9.183 ± 7.887 | 11.850 ± 9.440*** |
| Input | 5.740 ± 5.335 | 8.388 ± 7.433 | 12.511 ± 10.023** | |
| Output | 7.897 ± 7.042*** | 9.519 ± 7.423* | 10.549 ± 8.797 | |
| U-Net MTL (23.38 M) | No | 7.803 ± 7.488*** | 8.756 ± 7.244 | 11.560 ± 9.572 |
| Input | 5.478 ± 4.589 | 8.172 ± 7.710 | 12.130 ± 9.791 | |
| Output | 8.060 ± 7.562*** | 9.336 ± 7.810* | 11.983 ± 10.026 | |
| AA-MTL (36.59 M) | No | 8.078 ± 7.466*** | 9.385 ± 7.833** | 11.775 ± 9.144** |
| Input | 5.434 ± 4.402 | 8.347 ± 7.889 | 12.171 ± 10.284 | |
| Output | 7.613 ± 7.098*** | 8.190 ± 6.854 | 10.635 ± 8.256 | |
Best evaluation scores are presented in bold
RSNA Radiologic Society of North America, AMC Asan Medical Center, MAE mean absolute error, BA bone age, CA chronological age, MTL multi-task learning, AA auxiliary-accelerated
*p < 0.05; **p < 0.01; ***P < 0.001
aPaired t-test is applied to compare the performance between each method and best performance method in RSNA dataset
bWilcoxon signed-rank test is applied to compare the performance between each method and best performance method in AMC dataset
In the U-Net backbone architecture, the confounding adjustment by input method showed the best performances in the RSNA dataset with an MAE of 5.740 months (P-value < 0.001, no adjustment and adjustment by output). For the AMC dataset bone age, confounding adjustment by input showed statistically better performance than confounding adjustment by output (P-value = 0.023). For the AMC dataset chronological age, confounding adjustment by output outperformed no adjustment (P-value < 0.001) and adjustment by input (P-value = 0.002).
The confounding adjustment by input method showed the best performances in bone age estimation of the RSNA dataset when compared with the other methods (P-value < 0.001 in both methods) in the U-Net MTL architecture. For the AMC dataset bone age, a significant difference between the confounding adjustment by input and output (P-value = 0.027) was observed, whereas no statistical difference between input and no adjustment (P-value = 0.205) was observed. For the chronological age, there were no significant differences between the best performing method, no adjustment, and adjustment by input (P-value = 0.542) and output (P-value = 0.329).
Finally, in the proposed AA-MTL architecture, confounding adjustment by input outperformed other methods in the RSNA dataset with an MAE of 5.434 months (P-value < 0.001, no adjustment and adjustment by output). For the AMC dataset bone age, adjustment by output significantly outperformed no adjustment (P-value = 0.009). However, no significant difference between output and input was observed (P-value = 0.814). For the AMC dataset chronological age, adjustment by output outperformed no adjustment (P-value = 0.006), but not adjustment by input (P-value = 0.051).
Comparison of Conducting Multi-task at Diverse Encoder Level
The performance of each MTL network depended on the other tasks and model size [1, 41]. Considering the multi-task nature of this study, confounding adjustments and target task were conducted at the diverse encoder levels. Three different multi-task combinations of confounding adjustments and task were performed: sequential (sex classification at second encoder level, bone age estimation at bottleneck level), simultaneous (sex classification and bone age estimation at bottleneck level), and inverse-sequential (bone age estimation at second encoder level, sex classification at bottleneck level). The U-Net backbone architecture performed only sex classification and bone age estimation. The U-Net MTL and AA-MTL architectures performed sex classification, bone age estimation, and source image reconstruction from augmented images.
For the RSNA dataset bone age, the simultaneous model outperformed the inverse-sequential model (P-value = 0.007); however, it did not outperform the sequential model (P-value = 0.328) with double-task U-Net backbone architecture. In the AMC dataset, the simultaneous model outperformed the inverse-sequential model (P-value = 0.008) but not the sequential model (P-value = 0.075) with bone age labels; whereas the sequential model outperformed the inverse-sequential (P-value < 0.001) and simultaneous (P-value = 0.021) models with chronological age labels.
In the U-Net MTL architecture, the simultaneous model showed the best performance with an MAE of 7.601 months for the RSNA dataset bone age; however, no statistical difference was observed compared to the sequential (P-value = 0.080) or inverse-sequential (P-value = 0.281) models. In the AMC dataset, the simultaneous model outperformed both the inverse-sequential (P-value < 0.001) and sequential (P-value = 0.006) models with bone age labels, and the inverse-sequential model (P-value = 0.003) but not the sequential model (P-value = 0.148) with chronological age labels.
For the RSNA dataset bone age, the simultaneous model showed the best performance but did not have statistically significant results compared to the inverse-sequential (P-value = 0.115) or sequential (P-value = 0.249) models with AA-MTL architecture. For the AMC dataset with bone age labels, the sequential model of AA-MTL architecture showed the best performance with an MAE of 8.190 m. The AA-MTL sequential model significantly outperformed the inverse-sequential model (P-value = 0.001), but no statistical difference between it and the simultaneous model (P-value = 0.990) was observed. The sequential model of AA-MTL architecture showed the best performance for the AMC dataset with chronological age labels: it outperformed the inverse-sequential (P-value = 0.002) and simultaneous (P-value = 0.001) models. Table 2 summarizes the comparison results of conducting multi-task at diverse encoder level.
Table 2.
Comparison of conducting multi-task at diverse encoder level
| Sex classification | Bone age estimation | RSNA dataset | AMC dataset | |
|---|---|---|---|---|
| MAE (BA)a | MAE (BA)b | MAE (CA)b | ||
| U-Net backbone architecture | ||||
| Bottleneck | 2nd encoder | 8.883 ± 7.376** | 10.008 ± 7.570** | 12.202 ± 9.774*** |
| Bottleneck | 7.523 ± 7.174 | 8.690 ± 7.080 | 11.326 ± 8.507* | |
| 2nd encoder | Bottleneck | 7.897 ± 7.042 | 9.519 ± 7.423 | 10.549 ± 8.797 |
| U-Net MTL architecture | ||||
| Bottleneck | 2nd encoder | 8.509 ± 7.232 | 10.112 ± 7.870*** | 12.456 ± 9.643** |
| Bottleneck | 7.601 ± 7.427 | 8.477 ± 7.557 | 11.157 ± 9.816 | |
| 2nd encoder | Bottleneck | 8.060 ± 7.562 | 9.336 ± 7.810** | 11.983 ± 10.026 |
| AA-MTL architecture | ||||
| Bottleneck | 2nd encoder | 7.861 ± 5.866 | 9.500 ± 7.725** | 11.866 ± 9.441** |
| Bottleneck | 7.206 ± 6.647 | 8.351 ± 7.099 | 11.884 ± 9.046** | |
| 2nd encoder | Bottleneck | 7.613 ± 7.098 | 8.190 ± 6.854 | 10.635 ± 8.256 |
Best evaluation scores are presented in bold
RSNA Radiologic Society of North America, AMC Asan Medical Center, MAE mean absolute error, BA bone age, CA chronological age, MTL multi-task learning, AA auxiliary-accelerated
*p < 0.05; **p < 0.01; ***p < 0.001
aPaired t-test is applied to compare the performance between each method and best performance method in RSNA dataset
bWilcoxon signed-rank test is applied to compare the performance between each method and best performance method in AMC dataset
Comparison of Multiple Tasks in Performance and Generalizability
A comparison of the single-task model, which only performed bone age estimation; double-task model, which performed bone age estimation and source image reconstruction; and triple-task model, which performed bone age estimation, source image reconstruction, and sex classification is summarized in Table 3. In the U-Net MTL architecture, the double-task model with sex information showed the best performance in both datasets. In the AA-MTL architecture, the double-task model with sex information showed the best performance in the RSNA dataset. However, in the AMC dataset, the triple-task model showed the best performance with both bone age and chronological age labels.
Table 3.
Comparison of multiple tasks in performance and generalizability
| Architecture | Multiple task | RSNA dataset | AMC dataset | |
|---|---|---|---|---|
| MAE (BA)a | MAE (BA)b | MAE (CA)b | ||
| U-Net MTL | Single task (no sex) | 7.966 ± 6.693*** | 9.183 ± 7.887* | 11.850 ± 9.440 |
| Single task (sex) | 5.740 ± 5.335 | 8.388 ± 7.433 | 12.511 ± 10.023 | |
| Double task (no sex) | 7.803 ± 7.488*** | 8.756 ± 7.244 | 11.560 ± 9.572 | |
| Double task (sex) | 5.478 ± 4.589 | 8.172 ± 7.710 | 12.130 ± 9.791 | |
| Triple task | 8.060 ± 7.562*** | 9.336 ± 7.810* | 11.982 ± 10.026 | |
| AA-MTL | Single task (no sex) | 7.858 ± 8.351*** | 9.130 ± 7.865* | 11.762 ± 8.495** |
| Single task (sex) | 5.562 ± 5.368 | 8.323 ± 7.727 | 12.200 ± 9.937* | |
| Double task (no sex) | 8.078 ± 7.466*** | 9.385 ± 7.833** | 11.775 ± 9.144** | |
| Double task (sex) | 5.434 ± 4.402 | 8.347 ± 7.889 | 12.171 ± 10.284 | |
| Triple task | 7.613 ± 7.098*** | 8.190 ± 6.854 | 10.635 ± 8.256 | |
Best evaluation scores are presented in bold
RSNA Radiologic Society of North America, AMC Asan Medical Center, MAE mean absolute error, BA bone age, CA chronological age, MTL multi-task learning, AA auxiliary-accelerated
*p < 0.05; **p < 0.01; ***p < 0.001
aPaired t-test is applied to compare the performance between each method and best performance method in RSNA dataset
bWilcoxon signed-rank test is applied to compare the performance between each method and best performance method in AMC dataset
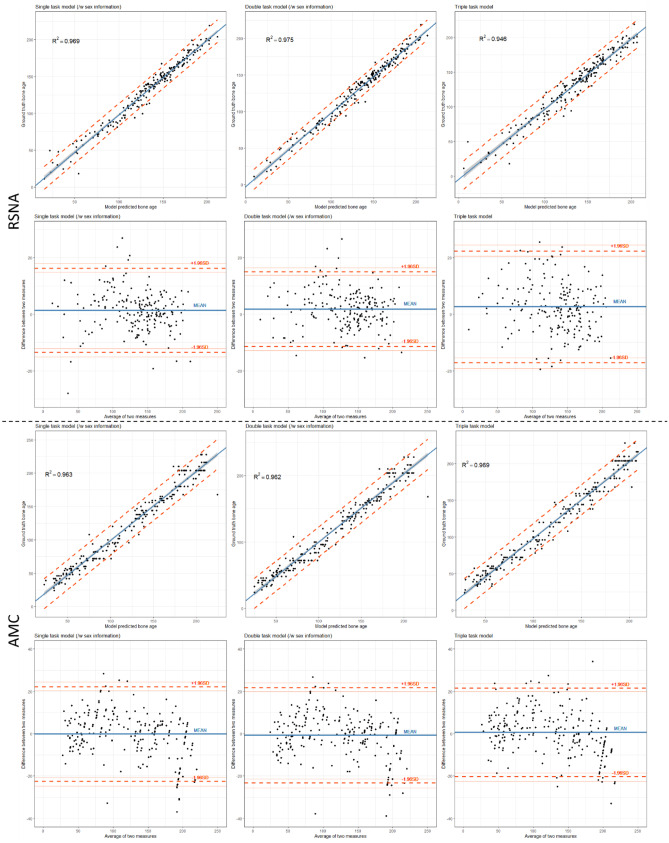
Correlation plot and Bland–Altman plot of each multi-task model in the AA-MTL architecture are depicted in Fig. 4. All three models showed decent performances in estimating bone ages, with R2 values of 0.969, 0.975, and 0.946 in the single-, double-, and triple-task models in the RSNA dataset, respectively. The Bland–Altman plot of all three models showed good agreement between the ground truth and model-predicted bone ages.
Fig. 4.
Correlation plot and Bland–Altman plot between ground truth bone age label of datasets and multi-task model-predicted bone age. The upper panel of the figure shows the results of the RSNA dataset, and the lower panel shows the results of the AMC dataset. Single task model with sex information, double task model with sex information, and triple task models are shown from the left to right
In the AMC dataset, all models showed decent performances in estimating bone ages, with R2 values of 0.963, 0.962, and 0.969 in the single-, double-, and triple-task models, respectively. The Bland–Altman plots of all three models showed good agreements between the ground truth and model-predicted bone ages, with mean differences of 1.382 (95% confidence interval [CI], –13.543–16.306), 1.827 (95% CI, –11.423–15.077), and 2.622 (95% CI, –17.146–22.391) for the single-, double-, and triple-task models in the RSNA dataset, respectively; additionally, they showed good agreements with mean differences of –0.198 (95% CI, –22.480–22.085), –0.759 (95% CI, –23.247–21.729), and 0.625 (95% CI, –20.298–21.548) in the AMC dataset, respectively.
Average Class Activation Map
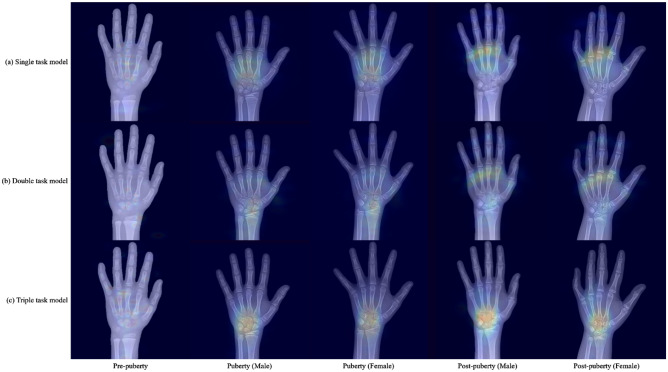
The qualitative results were evaluated using the average Grad-CAMs. Grad-CAMs acquired from each image were coordinated according to the representative image of each puberty group. Subsequently, the coordinated Grad-CAM images were averaged and superimposed on the representative images. The average Grad-CAM images acquired from the single-, double-, and triple-task models based on the AA-MTL architecture are depicted in Fig. 5.
Fig. 5.
Average Grad-CAM shown in each puberty group. All three models are based on AA-MTL architecture. Pre-puberty is defined as 0–6 years, puberty as 6–14 years for boys and 6–12 years for girls, and post-puberty as 14–18 years for boys and 12–18 years for girls
Discussions
We proposed and thoroughly investigated a novel method to exploit confounding variables in a non-linear deep learning model for bone age estimation in pediatric hand X-rays. All models used in this study estimated the bone age with a suitable R2 value. Additionally, all models highlighted the regions of interest, such as carpal bones, metatarsophalangeal joints, and distal epiphyses of radius and ulna, in averaged Grad-CAM. The results revealed that adjusting confounding variables by including additional input enhances internal performance, whereas adjusting confounding variables by prediction enhances generalizability of the external performance of a deep learning model. Additionally, the effect of the relationship between the encoder size and task hierarchy on adjustment performance was investigated through ablation studies. The results revealed that the proper encoder size and task hierarchy can improve model performance.
When training deep learning model, the balance between the model size, size of dataset, and difficulty of the target task is critical in the model performance. This explains the better performance of the AA-MTL model compared to the U-Net MTL model. In MTL, the combination of tasks affects the performances of the others [41] because the encoder shares the feature for each task. The extent of encoder sharing is critical in each task, particularly when main and auxiliary tasks exist [42]. Therefore, we interpreted that the hierarchical structure of MTL benefits the performance and generalizability of the main task using the latent representations extracted from the early shared encoder for auxiliary tasks, and additional representations extracted from the later independent encoder for the main task.
Our study has several advantages. First, we trained the model with an open dataset [26]; therefore, our internal results can be easily reproduced and compared with existing methods. Furthermore, we externally validated our method using the AMC dataset, which was collected from the Asian referral hospital. Therefore, our method shows robustness over multiple centers and multiple races, compared to human experts, who show mean age differences from 2.88 to 4.92 months [43]. Second, our model showed comparable performances without leveraging additional dense labeling [44, 45] or ensemble multiple models [46, 47]. Furthermore, the model that leveraged confounding variables as the output showed comparable results to the model that used them as input. Therefore, this study suggests that models trained to predict confounding variables can achieve additional performance even in the clinical situations where the confounding variables are absent or difficult to acquire. Third, we thoroughly investigated the effect of adjusting the confounding variable (sex) in a non-linear deep learning model through multiple ablation studies. We disclosed the properties of encoder size, task hierarchy, and multiple task combination acting on the performance and generalizability. Fourth, the age discrepancy between the model-estimated bone age and ground truth chronological age was compared. In the clinical context, the bone age estimation is used for adult height prediction, and anomaly detection in pediatric endocrinology [20, 24, 34] and genetics [19], which can be critical in real-world practice. When bone age estimation is properly trained with only normal pediatric hand X-rays, a large discrepancy between model-estimated bone age and chronological age may indicate a pathologic condition. Figure 6 depicts an example anomaly case superimposed with Grad-CAM. The ground truth chronological age for this case was 138 months; however, the model predicted 227.97 months. Carpal coalition, which can be associated with genetic syndromes, such as fetal alcohol syndrome or Turner syndrome [48, 49], was identified. Further studies with anomaly detection tasks are required to confirm this result. Finally, we addressed our qualitative results with averaged Grad-CAMs superimposed on representative images according to puberty stage. With this method, the overall explainability of each model was easily shown and “cherry picking” was reduced.
Fig. 6.
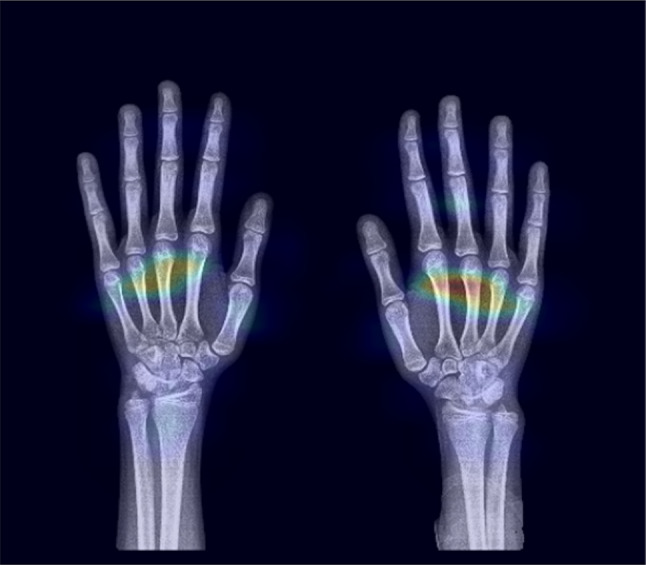
Example anomaly case with superimposed Grad-CAM. The ground truth chronological age is 138 months and the model predicted 227.97 months. Luno-triquetral coalition, a type of carpal coalition, exists in this case, which can be associated with genetic syndromes
However, our study had some limitations. First, considering the sensitive nature of medical data, access to our private external data is limited, which can reduce the reproducibility. Second, because a limited number of confounding variables was provided in the training dataset, only sex information was adjusted. Further studies adjusting more confounding variables, such as hormonal value and genetic and nutritional condition, are required to confirm our results. Furthermore, this study used only one external validation dataset and one internal validation dataset. Due to the sensitive nature of medical data, additional external validation datasets are difficult to acquire. Additional validation datasets with multiple prospective studies are required to confirm our results. Third, because adjusting the confounding variable in generalized linear models focuses on isolating the effect of independent variables, exploiting the confounding variable in a non-linear deep learning model could be different in this context. Finally, further ablation studies, such as multiple model architecture, confounding input level, decoder level, and multi-task weight ablations, were not performed owing to time limitations, GPU resources, and word limits.
Conclusion and Future Works
To estimate bone age in pediatric X-rays, the clinical setting and balance between model size, task hierarchy, and confounding adjustment method play important roles in performance and generalizability; therefore, a proper adjusting method of confounding variables to train deep learning-based models may be required for improved models. Further studies with additional ablation studies are required to find suitable combinations to improve performance and generalizability. In addition, further studies could be conducted to investigate the effects of multiple medical tasks on a variety of confounding variables.
Supplementary Information
Below is the link to the electronic supplementary material.
Acknowledgements
We thank Kyungjin Cho and Jun Soo Lee for their valuable discussion.
Author Contributions
All authors contributed to the study conception and design. Material preparation was performed by Ki Duk Kim, Sunggu Kyung and Miso Jang. Data collection was performed by Hee Mang Yoon. Data analyses were performed by Ki Duk Kim, Sunghwan Ji, and Dong Hee Lee. The first draft of the manuscript was written by Ki Duk Kim and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
This study was conducted by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (HI18C2383).
Data Availability
The RSNA dataset is publicly available at: https://www.rsna.org/education/ai-resources-and-training/ai-image-challenge/rsna-pediatric-bone-age-challenge-2017.
Declarations
Conflicts of Interest
The authors report no conflicts of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Hee Mang Yoon and Namkug Kim these corresponding authors contributed equally.
Contributor Information
Hee Mang Yoon, Email: espoirhm@gmail.com, Email: hmyoon@amc.seoul.kr.
Namkug Kim, Email: namkugkim@gmail.com.
References
- 1.Goodfellow, I., Y. Bengio, and A. Courville, Deep learning. 2016: MIT press.
- 2.Szegedy, C., et al. Going deeper with convolutions. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2015.
- 3.He, K., et al. Deep residual learning for image recognition. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
- 4.Raghu, V.K., et al., Deep learning to estimate biological age from chest radiographs. JACC: Cardiovascular Imaging, 2021. 14(11): p. 2226–2236. [DOI] [PMC free article] [PubMed]
- 5.Korot E, et al. Predicting sex from retinal fundus photographs using automated deep learning. Scientific reports. 2021;11(1):1–8. doi: 10.1038/s41598-021-89743-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wu, L., et al., Effect of a deep learning-based system on the miss rate of gastric neoplasms during upper gastrointestinal endoscopy: a single-centre, tandem, randomised controlled trial. 2021. 6(9): p. 700–708. [DOI] [PubMed]
- 7.Rajpurkar P, et al. Deep learning for chest radiograph diagnosis: A retrospective comparison of the CheXNeXt algorithm to practicing radiologists. 2018;15(11):e1002686. doi: 10.1371/journal.pmed.1002686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nelder, J.A. and R.W.J.J.o.t.R.S.S.S.A. Wedderburn, Generalized linear models. 1972. 135(3): p. 370–384.
- 9.Robinson LD, et al. The effects of covariate adjustment in generalized linear models. 1998;27(7):1653–1675. [Google Scholar]
- 10.Shpitser, I., T. VanderWeele, and J.M.J.a.p.a. Robins, On the validity of covariate adjustment for estimating causal effects. 2012.
- 11.Pourhoseingholi MA, et al. How to control confounding effects by statistical analysis. 2012;5(2):79. [PMC free article] [PubMed] [Google Scholar]
- 12.Kahlert, J., et al., Control of confounding in the analysis phase–an overview for clinicians. 2017. 9: p. 195. [DOI] [PMC free article] [PubMed]
- 13.McPherson S, et al. Age as a confounding factor for the accurate non-invasive diagnosis of advanced NAFLD fibrosis. 2017;112(5):740. doi: 10.1038/ajg.2016.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wu AH, et al. Association of obesity and survival in systolic heart failure after acute myocardial infarction: potential confounding by age. 2010;12(6):566–573. doi: 10.1093/eurjhf/hfq043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Reeves MJ, Lisabeth LDJN. The confounding issue of sex and stroke. 2010;74(12):947–948. doi: 10.1212/WNL.0b013e3181d5a4bc. [DOI] [PubMed] [Google Scholar]
- 16.Young, R.P., et al., COPD prevalence is increased in lung cancer, independent of age, sex and smoking history. 2009. 34(2): p. 380–386. [DOI] [PubMed]
- 17.Tanner, J., et al., Prediction of adult height from height and bone age in childhood. A new system of equations (TW Mark II) based on a sample including very tall and very short children. Archives of disease in childhood, 1983. 58(10): p. 767–776. [DOI] [PMC free article] [PubMed]
- 18.Tanner J, et al. Prediction of adult height from height, bone age, and occurrence of menarche, at ages 4 to 16 with allowance for midparent height. Archives of disease in childhood. 1975;50(1):14–26. doi: 10.1136/adc.50.1.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gkourogianni A, et al. Clinical characterization of patients with autosomal dominant short stature due to aggrecan mutations. 2017;102(2):460–469. doi: 10.1210/jc.2016-3313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rosenfeld RG, et al. Diagnostic controversy: the diagnosis of childhood growth hormone deficiency revisited. The Journal of Clinical Endocrinology & Metabolism. 1995;80(5):1532–1540. doi: 10.1210/jcem.80.5.7538145. [DOI] [PubMed] [Google Scholar]
- 21.KAPLAN, S.L. and M.M. GRUMBACH, CLINICAL REVIEW 14 Pathophysiology and Treatment of Sexual Precocity. The Journal of Clinical Endocrinology & Metabolism, 1990. 71(4): p. 785–789. [DOI] [PubMed]
- 22.Allen DB. Growth suppression by glucocorticoid therapy. Endocrinology and metabolism clinics of North America. 1996;25(3):699–717. doi: 10.1016/S0889-8529(05)70348-0. [DOI] [PubMed] [Google Scholar]
- 23.Vasseur, F., et al., Nutritional status and growth in pediatric Crohn's disease: a population-based study. Official journal of the American College of Gastroenterology| ACG, 2010. 105(8): p. 1893–1900. [DOI] [PubMed]
- 24.de Zegher F, et al. Growth failure in children with systemic juvenile idiopathic arthritis and prolonged inflammation despite treatment with biologicals: Late normalization of height by combined hormonal therapies. Hormone Research in Paediatrics. 2018;90(5):337–343. doi: 10.1159/000489778. [DOI] [PubMed] [Google Scholar]
- 25.Thommessen M, Heiberg A, Kase B. Feeding problems in children with congenital heart disease: the impact on energy intake and growth outcome. European journal of clinical nutrition. 1992;46(7):457–464. [PubMed] [Google Scholar]
- 26.Halabi SS, et al. The RSNA pediatric bone age machine learning challenge. 2019;290(2):498. doi: 10.1148/radiol.2018180736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Beheshtian, E., et al., Generalizability and bias in a deep learning pediatric bone age prediction model using hand radiographs. 2022: p. 220505. [DOI] [PubMed]
- 28.Arisaka O, et al. Preliminary report: effect of adrenal androgen and estrogen on bone maturation and bone mineral density. 2001;50(4):377–379. doi: 10.1053/meta.2001.21678. [DOI] [PubMed] [Google Scholar]
- 29.Larson DB, et al. Performance of a deep-learning neural network model in assessing skeletal maturity on pediatric hand radiographs. 2018;287(1):313–322. doi: 10.1148/radiol.2017170236. [DOI] [PubMed] [Google Scholar]
- 30.Greulich, W.W. and S.I. Pyle, Radiographic atlas of skeletal development of the hand and wrist. 1959: Stanford university press.
- 31.Kim, K.D., et al., Enhancing deep learning based classifiers with inpainting anatomical side markers (L/R markers) for multi-center trials. 2022. 220: p. 106705. [DOI] [PubMed]
- 32.Ronneberger, O., P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. in International Conference on Medical image computing and computer-assisted intervention. 2015. Springer.
- 33.Selvaraju, R.R., et al. Grad-cam: Visual explanations from deep networks via gradient-based localization. in Proceedings of the IEEE international conference on computer vision. 2017.
- 34.Cohen, P., et al., Consensus statement on the diagnosis and treatment of children with idiopathic short stature: a summary of the Growth Hormone Research Society, the Lawson Wilkins Pediatric Endocrine Society, and the European Society for Paediatric Endocrinology Workshop. 2008. 93(11): p. 4210–4217. [DOI] [PubMed]
- 35.De Onis, M., et al., Comparison of the WHO child growth standards and the CDC 2000 growth charts. 2007. 137(1): p. 144–148. [DOI] [PubMed]
- 36.De Onis M, et al. Worldwide implementation of the WHO child growth standards. 2012;15(9):1603–1610. doi: 10.1017/S136898001200105X. [DOI] [PubMed] [Google Scholar]
- 37.Altman, D.G. and J.M.J.J.o.t.R.S.S.S.D. Bland, Measurement in medicine: the analysis of method comparison studies. 1983. 32(3): p. 307–317.
- 38.Bland, J.M. and D.J.T.l. Altman, Statistical methods for assessing agreement between two methods of clinical measurement. 1986. 327(8476): p. 307–310. [PubMed]
- 39.He, K., et al., Masked autoencoders are scalable vision learners. 2021.
- 40.DeVries, T. and G.W.J.a.p.a. Taylor, Improved regularization of convolutional neural networks with cutout. 2017.
- 41.Standley, T., et al. Which tasks should be learned together in multi-task learning? in International Conference on Machine Learning. 2020. PMLR.
- 42.Misra, I., et al. Cross-stitch networks for multi-task learning. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
- 43.Zhang A, et al. Racial differences in growth patterns of children assessed on the basis of bone age. 2009;250(1):228–235. doi: 10.1148/radiol.2493080468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Escobar, M., et al. Hand pose estimation for pediatric bone age assessment. in International conference on medical image computing and computer-assisted intervention. 2019. Springer.
- 45.Lee H, et al. Fully automated deep learning system for bone age assessment. 2017;30(4):427–441. doi: 10.1007/s10278-017-9955-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pan, I., et al., Improving automated pediatric bone age estimation using ensembles of models from the 2017 RSNA machine learning challenge. 2019. 1(6). [DOI] [PMC free article] [PubMed]
- 47.Liu R, et al. Coarse-to-fine segmentation and ensemble convolutional neural networks for automated pediatric bone age assessment. 2022;75:103532. [Google Scholar]
- 48.Gottschalk MB, Danilevich M, Gottschalk HPJH. Carpal coalitions and metacarpal synostoses: a review. 2016;11(3):271–277. doi: 10.1177/1558944715614860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pruszczynski B, et al. Incidence of carpal coalition in the pediatric population. 2016;36(8):e106–e110. doi: 10.1097/BPO.0000000000000639. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The RSNA dataset is publicly available at: https://www.rsna.org/education/ai-resources-and-training/ai-image-challenge/rsna-pediatric-bone-age-challenge-2017.