Abstract
Airway diseases are frequently related to morphological changes that may influence lung physiology. Accurate airway region segmentation may be useful for quantitative evaluation of disease prognosis and therapy efficacy. The information can also be applied to understand the fundamental mechanisms of various lung diseases. We present a hybrid method to automatically segment the airway regions on 3D volume chest computed tomography (CT) scans. This method uses multi-scale filtering and support vector machine (SVM) classification. The proposed scheme is comprised of two hybrid steps. First, a tubular structure-based multi-scale filter is applied to find the initial candidate airway regions. Second, for identifying candidate airway regions using the fuzzy connectedness technique, the small and disconnected branches of airway regions are detected using SVM classification trained to differentiate between airway and non-airway regions through texture analysis of user-defined landmark points. For development and evaluation of the method, two datasets were incorporated: (1) 55 lung-CT volumes from the Korean Obstructive Lung Disease (KOLD) Cohort Study and (2) 20 cases from the publicly open database (EXACT′09). The average tree-length detection rates of EXACT′09 and KOLD were 56.9 ± 11.0 and 70.5 ± 8.98, respectively. Comparison of the results for the EXACT′09 data set between the presented method and other methods revealed that our approach was a high performer. The method limitations were higher false-positive rates than those of the other methods and risk of leakage. In future studies, application of a convolutional neural network will help overcome these shortcomings.
Keywords: Airway segmentation, Frangi filter, Top-hat transform, Support vector machine, Hybrid filtering, Fuzzy connectedness
Introduction
Quantitative analysis of the airway region has become possible owing to the rapid development in computed tomography (CT) imaging technology. Quantitative information about the airway structure plays an important role in the decision-making steps and diagnosis of diseases such as pneumothorax and asthma [1]. Furthermore, extraction of airway regions is also helpful for other segmentation steps, such as the lobes, nodules, and the entire lung. Another application of airway region extraction is the virtual bronchoscopy method, which is typically used to establish a planning guideline for bronchoscopic navigation [2, 3]. An accurate segmentation technique can provide essential information for diagnosis and surgery to physicians. However, accurate extraction of airway regions is difficult because of the complex branching structure, large variability of scales, and the proclivity for the presence of motion artifacts. These reasons hinder the use of quantitative airway segmentation in clinical settings. Delineation of airway boundaries can be performed using manual or semi-automatic programs. However, these approaches are subject to intra- and inter-user variability owing to the stiff learning curve and require several hours to complete. Therefore, there is a need for the development of an automatic segmentation technique [4–8].
Development of automatic airway segmentation methods on the basis of CT images is difficult and complicated. The Hounsfield unit (HU) value distribution of the airway region is unstable because of the high noise levels in the small airway lumen. In addition, leakage to lung parenchyma often occurs because of low contrast between the density of airway walls and lung parenchyma. Moreover, the region between the bronchial wall and pulmonary blood vessels has an intensity distribution similar to that of the airway regions. These leakage regions can be considered as false positives (FPs) in airway segmentation.
Many studies have focused on the automatic bronchial awareness obtained from 3D chest CT volumes. Lo et al. [9] summarized the airway segmentation approach through a challenge called EXACT′09, which shows various airway region segmentation algorithms.
The 3D region-growing algorithm is the most common and widely used approach that uses thresholds of CT images and does not require prior knowledge of airway regions, such as the shape, size, and orientation of the small bronchi [10–13]. Kitasaka et al. [14], Mori et al. [11], Tschirren et al. [15], and Feuerstein et al. [16] used approaches based on region-growing algorithms with appropriate threshold adjustment to extract airway regions. Schlathoelter et al. [17] achieved airway region segmentation based on the forward propagation method. Lo et al. [18] introduced an approach that could segment the airway regions from 3D CT volumes using a trained airway appearance model, directional information of airway regions, and a region-growing approach.
However, owing to the low contrast of peripheral airway branches, the region-growing approach is effective for extracting large airway branches including the trachea and the main bronchus; however, leakage while using the region-growing approach is often a problem. Some researchers have developed a graph-based method to connect the disconnected small branches and reduce false-positive regions (FPRs). Bauer et al. [19] proposed a graph-based approach for airway segmentation from CT scans and validated the performance of different feature categories and feature combinations of five lung cohorts. This method can achieve a high detection rate of airway regions, but the high number of FPRs remains a problem.
Several researchers have developed an approach based on classification to avoid and reduce the leakage regions of airway region segmentation. Lo et al. [20] used a k-NN classifier that was trained to distinguish between airway regions and non-bronchial voxels and then used the growing region to finish airway region segmentation. Although this method can effectively avoid leakage, it has not been able to extract the small bronchi. To track smaller bronchi, a tubular structure-enhancement filter approach was introduced in the current study. Recently, several studies have adopted this approach. Yano et al. [21] proposed an approach for detecting bronchus candidate regions using a tube-intensifying filter based on a local intensity structure. This method can effectively detect the locations of bronchi, but a high number of FP lung regions are inevitable. Ziyue et al. [22] proposed a computational framework to quantify airways through the tubular structure-enhancement filter approach for segmentation of the lumen that used a spatially constrained Markov random-walk method and a relative fuzzy connectedness method to estimate the airway wall thickness. This method can lower the number of FP regions, but it was not able to detect small bronchi. Qier et al. [23] developed a method for detecting airway candidate regions using a multi-scale tube-like structure filter and used an SVM classifier trained to distinguish between voxels belonging to true-positive and FP regions and then used a graph-cut algorithm to complete airway segmentation. This method can effectively detect the locations of bronchi and remove FP regions. However, this method requires a relatively long computation time.
In this paper, we propose a technique that uses a filter that can detect tubular structures and machine learning to accurately extract airway regions while reducing FP regions. This approach tracks and detects candidate airway regions by taking into account the densities of and cavity-like structures within the CT images. The method uses two types of tube-enhancement filters to detect the candidate airway regions in the CT images. In addition, a classifier was constructed to classify an appropriate candidate and included a directional tube and deletion of the FP regions using conventional features and tube-like structure-based features. In the current study, 55 cases were evaluated to validate our proposed technique. The detection performance and FP rates were compared with those of the previously described methods and the EXACT′09 public results.
Materials and Methods
Dataset
KOLD Cohort Group
All patients included in this study were chosen from the Korean Obstructive Lung Disease (KOLD) cohort, which includes 226 stable patients with obstructive lung disease who were prospectively obtained from the pulmonary clinics of 11 hospitals in South Korea between June 2005 and December 2009. The inclusion criteria of the KOLD cohort have been previously described [7, 24]. Chronic obstructive pulmonary disease (COPD) was diagnosed on the basis of airflow limitations that are not fully reversible (postbronchodilator forced expiratory volume in 1 s/forced vital capacity < 70% and smoking history of > 10 pack-years). Of 193 patients who met our diagnostic criteria for COPD, we excluded 22 patients with physician-diagnosed asthma. Finally, 65 COPD patients who had undergone volumetric CT using the same type of scanner at 7 select hospitals were randomly included in this study, which was approved by the institutional review boards of all 11 hospitals, and each patient provided written informed consent. The size of each slice scan was 512 × 512 pixels with a pixel size in the range of 0.525–0.783 mm. There was a different number of slices in each dataset (range 378–598 slices) with varying coverage. The thickness of all datasets was 0.700 mm. In our experiment, the dataset was divided into two groups. In the first dataset, there were 10 cases for training. In the second dataset, there were 55 cases for testing. The specifications of the CT volumes in the KOLD cohort group have been presented in Table 1. We used the first dataset for training to determine the parameters of the proposed method and for generating the training region of interest (ROI) patches by using user-defined landmarks. The second dataset was only used as the testing dataset for evaluating the segmentation results on the basis of determined parameters and user-defined landmarks.
Table 1.
The specifications of the CT volumes in KOLD cohort group
| Training dataset (10 case) | Test dataset (55 case) | |
|---|---|---|
| Image size (voxels) | 512 × 512 | 512 × 512 |
| Number of slices | 478–562 | 378–598 |
| Pixel spacing (mm) | 0.586–0.783 | 0.525–0.742 |
| Slice spacing (mm) | 0.699–0.700 | 0.699–0.700 |
| Reconstruction kernel | B30f | B30f |
EXACT′ 09 Public Dataset
Quantitative comparison of the proposed method with other methods is important. Therefore, we applied the method to the EXACT′09 public dataset of 20 test cases that were originally designed to compare the performance of different segmentation algorithms and provide the same performance measures for these cases. The size of each slice scan was 512 × 512 pixels with a pixel size in the range of 0.555–0.781 mm. There was a different number of slices in each dataset (range 267–675 slices) with varying thicknesses ranging from 0.500 to 1.000 mm. In our experiment, this dataset was used only as a test dataset. The specifications of the CT volumes in the EXACT′09 public dataset are shown in Table 2.
Table 2.
The specifications of the CT volumes in EXACT’ 09 public dataset
| Test dataset (20 case) | |
|---|---|
| Image size (voxels) | 512 × 512 |
| Number of slices | 267–675 |
| Pixel spacing (mm) | 0.555–0.781 |
| Slice spacing (mm) | 0.500–1.000 |
| Reconstruction kernel | B30f, B50f, B60f, B70f, B70s, FC10, FC12, Std, B, C, D |
CT Scan Protocol
KOLD Cohort Group
Volume CT scans were acquired without bronchodilatation within a day of pulmonary function testing (PFT). All CT scans were obtained using a 16-MDCT scanner (Somatom Sensation; Siemens Medical Systems, Erlangen, Germany). Scan parameters included 100 eff. mAs, 140 kVp, 16 × 0.75 mm collimation, and pitch equal to 1. Before performing the CT scans, the patients were instructed by the technician to hold their breath at full inspiration and expiration and were trained to ensure that full inspiration and expiration could be obtained. All CT scanners were calibrated every month after maintenance using water as the standard phantom; all machines were calibrated daily using air. We obtained all scans < 24 h after air calibration. Imaging data were stored in the Digital Imaging and Communications in Medicine (DICOM) format.
EXACT′09
The acquisition parameters of the 20 test data sets were as follows: Dosage was indicated as X-ray tube current (kVp) and exposure (mAs) pairs. The breathing status was full inspiration (Insp.) or full-expiration (Exp.). Contrast meant that it was used to acquire the intravenous contrast. The X-ray tube current and exposure ranged from 10 to 441 kVp and 5–6209 mAs, respectively. The abbreviations for the scanner vendors were as follows: Siemens Sensation (SS), Siemens Volume Zoom (SVZ), GE LightSpeed (GEL), Philips Brilliance (PB), Philips Mx8000 IDT (PMI), and Toshiba Aquilion (TA).
Overall Procedure
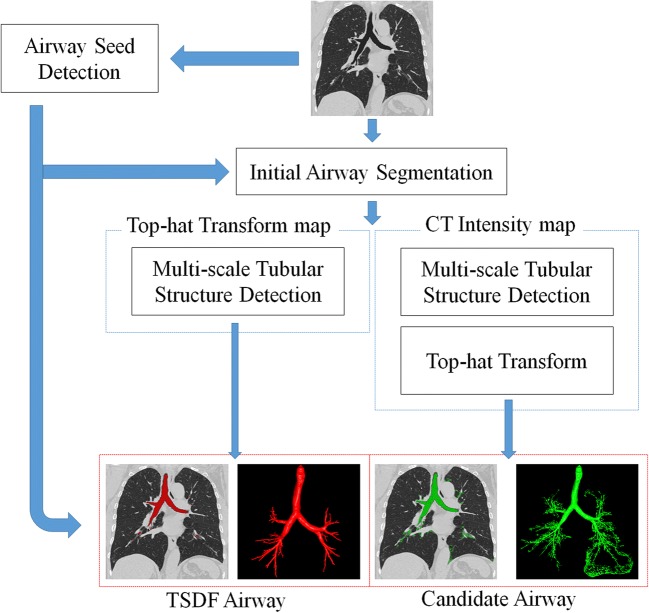
We designed a method to segment airway regions by combining multiple strategies to achieve low false negatives and FPs. The flowchart of the proposed method is shown in Fig. 1. First, an airway seed point in the trachea was detected automatically by modified 2D Hough transform [25]; then, two enhancement techniques of tubular structure were performed on 3D chest CT images simultaneously: a gray-scale morphological operation and a Tubular Structure Detection (TSD) [22, 26, 27]. Then, using the SVM classifier, we further searched for weak-contrast small airway regions and disconnected regions that were not detected by the two enhancement techniques. Our motivation for this multi-step combination was to identify other small airway regions and suppress FPs at the same time.
Fig. 1.
Flowchart of the hybrid enhancement filtering
Preprocessing
Sometimes, the minimum density value of the input CT volume was < 1024 HU value. To eliminate these noises, all values < 1024 HU were forcibly set to − 1024 HU.
Hybrid Enhancement Filtering
Detection of Initial Airway Region
Initial airway regions are typically well-contrasted in chest CT images. We performed a thresholding technique to a range of − 1024 HU to a specific threshold value. This value is typically − 950 HU. Then, the initial airway region was obtained using a connected component labeling technique and a detected airway seed. We obtained the refinement initial airway using a morphological operation and fill-hole algorithm [28].
Detection of Airway Region Using Hybrid Enhancement Filtering (HEF)
Tubular structure enhancement algorithms are employed to enhance tubular structure identification and delineation [22, 26, 27]. In the mathematical morphology theorem, the closing filter can be used to fill holes and remove dents that are smaller than a specific morphological structure size. The difference between the closed image and the original image, called the Black top-hat transform image, can reveal small structures that were eliminated after applying the closing filter [27]. Different radii of airway regions are dealt with by successive dilation of a range of morphological structuring elements
| 1 |
where δ0 is the smallest structuring element, δn is the result of n times dilation of δ0, and ⊕ is the morphological dilation operator.
| 2 |
where ⊖ is the morphological erosion operator. Further, a process is performed on τn as f = ∑nmax (τn − I) to a range of n ∈ {0.5, 1.0, 1.5, 2.0, 2.5} for detecting small- and mid-size branches of airway regions. The combining top-hat transform image f identifies potential locations of airway regions, and the process is performed by combining maximum responses from different ranges. Analyzing the Hessian matrix (second-order information) of a Gaussian filtered image provides local structural information. Eigenvalue decomposition is exactly performed on the Hessian matrix, and the resulting ordered eigenvalues, i.e., (λ1 ≤ λ2 ≤ λ3), are inspected. Particularly, it is expected that λ1 is small, whereas λ2 and λ3 are of equal and large sign that indicate whether the tubular structure is brighter or darker than background within voxels of the structure. Definitely, the TSD can be formulated as
| 3 |
for an original image and top-hat transform field,
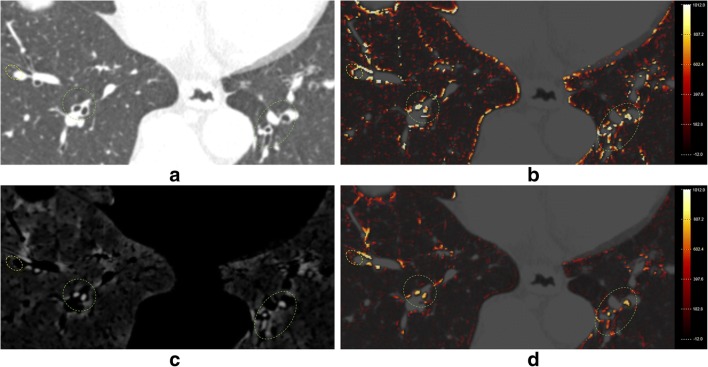
The above measures for TSD are calculated at different scale factors (σ), and the maximum response is achieved. So, we can obtain not only the optimal value but also the approximate local tubular structure scale for each voxel by using a multi-scale approach that covers a range of tubular structure widths and find the maximum response value V = max(Vσ), σmin ≤ σ ≤ σmax. We also performed TSD filtering on the black top-hat transformed result, HEF. The HEF response of airway regions is more powerful since it already enhanced the small airway regions and reduced the noise around them. One of the representative HEF results is shown in Fig. 2. Additionally, the operational parameters of all filters were fine-tuned in the training dataset.
Fig. 2.
Illustration of various filtering a CT image, b Frangi filtering, c Top-hat transform, and (d) HEF. An FP region around the airway region in the green dot circle of panel d is less than the green dot circle of panel b. An FP region connected to the airway region in the yellow dot circle of d is a weaker response than that of the green dot circle of b
Generating the Directional Tube by Using Fuzzy Connectedness
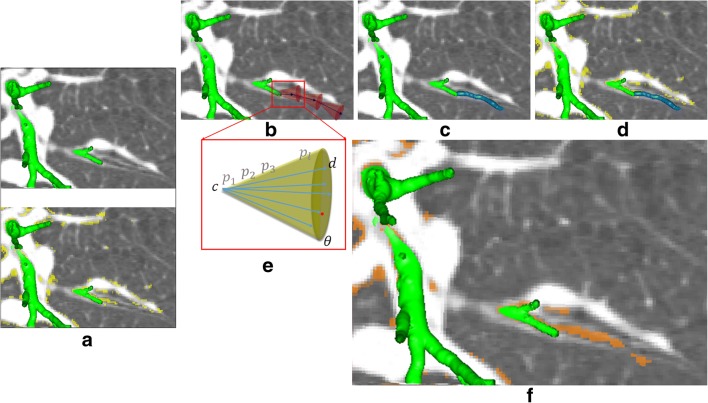
To increase the detection rate of small branches and reduce computation time at the SVM classification, we incorporated the directional tube algorithm. The algorithm can be performed in the following procedures. At first, the initial airway regions were extracted by two types of filters, and the range of threshold values for the directional tube algorithm was defined. Then, the skeletonization algorithm was applied to the initial airway candidate regions, and the end points of each airway region were detected [29, 30]. The initial direction of the endpoint was found by increasing the radius of the sphere shape from each point within the skeletonized binary mask. The fuzzy connectedness was calculated on the circular region perpendicular to the direction of the airway endpoint, and then the location of maximum fuzzy connectedness was found. The next circular region was prepared perpendicular to the direction of the maximum point from the current location, and the fuzzy connectedness of the next circular region was computed. This process was fulfilled iteratively.
The degree of the fuzzy connectedness between any two voxels c and d is considered to be the maximum of the strengths of all trajectories between c and d. An affinity relation k is the principal measure of local hanging togetherness of adjacent voxels. For a trajectory π, which is a set of voxels {p1, p2, p3, …, pl} with every two consecutive voxels being nearby, given fuzzy affinity function μk(pi, pi + 1), the strength of the trajectory is defined as the minimum affinity along the trajectory, so then the strength of connectedness μα(c, d) between any two voxels c and d is the strength of the most powerful trajectory between them as:
where p(c, d) indicate the set of all trajectories between c and d. An efficient computational solution is presented [31]. The performance of the fuzzy connectedness algorithm depends on the selection of the affinity function. The leading affinities used so far are a combination of adjacency μα, region feature μ∅, and homogeneity μψ such that fuzzy affinity is defined as
where μ∅(c, d) defines the hanging togetherness of c and d in the target region based on the togetherness of their feature values to the expected feature distribution of the target region. For homogeneity, affinity μψ(c, d) denote the homogeneity between c and d, with a higher value for pairs with similar voxel density. The affinity function can be formulated differently; however, for the common adjacency term, one can choose to use region feature, or homogeneity, or both. The general form of μ∅(c, d) and μψ(c, d) are expressed as
where σ is the standard deviation used for setting the line connecting the position of the circular region and the end point in the image density function, m is the mean value, and f indicates the image intensity function. We find the locations θ of the circular region C with the maximum fuzzy connectedness and perform this procedure iteratively to obtain the final directional tube. Figure 3 shows the procedure of the fuzzy-connectedness-based directional tube. Connecting the locations with maximum fuzzy connectedness collectively could cover some disconnected or not detect the small branches in the candidate airway.
Fig. 3.
Illustration of fuzzy connectedness-based directional tube. a Top: HEF filter map; bottom: candidate airway mask. b Path generation within pre-defined circular region that is perpendicular to the direction at the endpoint. c Directional tube with the maximum fuzzy connectedness. d Directional tube and candidate airway region. e Description of fuzzy connectedness calculation. f Final candidate airway region
Generating HEF Airway
The HEF airway region was obtained by using a thresholding technique in the two-type filtered image map. The thresholding value was selected experimentally. Then, the HEF airway region was detected by a connected component labeling using an airway seed [28]. Finally, we combined the directional tube and candidate airway regions, and then performed the connected component labeling with an airway seed point. The final candidate airway region with the directional tube was used to test the dataset of the SVM classifier for SVM-based additional candidate search (ACS) and FP Reduction (FPR).
SVM-Based Additional Candidate Search (ACS) and FP Reduction (FPR)
In this section, we devised a machine learning approach to further include small airway branches by classifying each location of the airway candidate regions into two classes: airway and non-airway. The classification-based method is described in the following. First, the dataset and evaluation setup are presented, and the quantitative image features are explained. Finally, the SVM classifier with Gaussian RBF (radial basis function) kernel and the description of how to combine the classification results are shown.
Data Set Generation for Training and Testing
The training datasets were retrieved from 10 patients. In each CT scan, 50 non-airway and 100 airway points were found by an experienced user. The rectangular shaped ROIs of 3 × 3 × 3, 7 × 7 × 7, and 11 × 11 × 11 voxels on CT images were generated around each landmark point for airway or non-airway. Two representative patterns of airway and non-airway region ROIs are shown in Fig. 4. We applied the trained classifier to the final airway candidate region with the directional tube for testing.
Fig. 4.

Representative ROIs around landmark points, a. ROIs from airway, b. ROIs from non-airway regions
Feature Extraction
In each ROI, 21 conventional textural and shape features and the semantic features for detecting airway regions shown to be effective in classifying airway regions were computed [32–34]. These conventional features were divided into five descriptors: histogram, gradient, run-length matrix, co-occurrence matrix, and moment. The histogram was defined by the number of voxels in each ROI with a given density. The gradient was defined as a change in density level from black to white, and a high gradient value was defined as a sharp change in gray level from black to white. The run-length matrix evaluates the texture based on the execution of gray tones, and the coarse and fine textures are defined as constant gray values and small numbers during execution, respectively. Other features describing the spatial dependence of gray-scale distributions were derived from the set of co-occurrence matrices that characterized the spatial gray-tone relationships in texture patterns and was calculated for each ROI. The bin sizes of run-length matrices and co-occurrence matrices representing the textural characteristics of an ROI were optimized to 32 and 64, respectively [32]. Since conventional features do not capture the shape of the tubular pattern, five additional descriptors for tubular structure were included: Hessian matrix, top-hat transform, tubular structure detection filter (TSDF), strain energy filter, and fuzzy connectedness. The 28 dimensions of a conventional feature vector and the additional five descriptors for each ROI are summarized in Table 3.
Table 3.
The 28 dimensional feature vectors
| Descriptor | Dimension |
|---|---|
| Histogram |
Mean S.D. Skewness Kurtosis Energy Entropy |
| Gradient |
Mean S.D. |
| Run-length |
Short-run emphasis (SRE) Long-run emphasis (LRE) Low gray-level emphasis (LRGE) High gray-level emphasis (HRGE) Run percentage (RP) |
| GLCM |
Angular second moment Contrast Correlation Inverse difference moment Entropy |
| Moment | J1, J2, J3 |
| Top-hat transform | Black top-hat mean |
| Hessian matrix | Mean |
| Fuzzy connectedness | Mean |
| Strain energy filter | Mean |
| HEF | Mean |
Strain Energy Filter
A strain energy filter was based on a decomposition of the strain energy, structure strength and shape, and measurement of the intensity contrast. These measures were combined with a density continuity term along the tubular structure and a step edge suppression term. Details have been previously reported [35, 36].
Fuzzy Connectedness
For the algorithm discussed in this paper [22, 31], the fuzzy connectedness algorithm (detail is in the Generating The Directional Tube Using Fuzzy Connectedness subsection) has the capability to combine three different features (top-hat transform, Hessian filtering, and affinity relation) within the same formulation. The affinity relation function can be formulated differently depending on the specific objective. Moreover, the common adjacency term can capture homogeneity, object features, or both. Three features are available to describe intensity, gray-scale morphological reconstructed results, and tubular structure measurements.
SVM Classification
We incorporated SVM for this binary classification problem. SVM constructs a hyper-plane, which can be used for classification. Let {x1, x2, x3, …, xn} be training data with d-dimensions and corresponding labels {y1, y2, y3, …, yn}, where yi ∈ {−1, 1}. We can choose the hyperplane so that the distance from it to the nearest data point on each side is maximized. If such a hyperplane exists, it is known as the maximum-margin hyper-plane and the linear classifier it defines is known as a maximum margin classifier [37]. The training instances that are placed closest to the hyper-plane are called support vectors. All support vectors placing on one side of the hyper-plane are labeled as − 1, and all support vectors placing on the other side are labeled as + 1. To construct an optimal hyper-plane, SVM uses an iterative training algorithm, which is used to minimize an error function.
In the experiments described in this paper, the Gaussian RBF kernel was applied. Because of its non-linearity, this kernel is appropriate for some non-separable data [38–40]. The classification result is a label image with values of − 1 for non-airway and + 1 for airway regions.
Generating Final Airway
The final airway region is obtained by performing the connected component labeling technique using the initial airway seed point on the combined regions from the HEF and the classified results.
Results
To obtain the training ROI patches in the machine learning part and also for the validation of the experimental results, we performed manual segmentation of 55 cases. Obtaining the ground truth for the whole dataset was extremely exhausting and time-consuming. The ground-truth data were entirely obtained from initial automatic segmentation and manual editing by experienced users who used commercial software developed by Caroline Soft Inc. It takes nearly 2–4 h for manual segmentation, including editing of each case.
The operational parameters in this study were selected experimentally as follows. For the morphological structure analysis, the multiple scale parameter σ was selected with values ranging from 0.5 to 2.5 mm with a step size of 0.5 mm. The parameter σ used in HEF was chosen according to the top-hat transform map. The parameter σ decides the diameters of the morphological cavity of the airway branch that this filter can enhance. By selecting different values of σ, the HEF can enhance the airway with different diameters.
In the Hessian analysis, the parameters α, β, and γ were set to 0.05, 10.0, and 100.0, respectively. For the fuzzy connectedness-based directional tube, the radius of the circular region was 3 mm, and the distance between the start point and circular region was 3 mm. The ranges of the threshold values of the HEF and top-hat transform map with small diameters were 300–1024 HU and 40–1024 HU. The candidate airway regions with directional tube were classified into FN and FP classes using the SVM classifier by local intensity information with 32 × 32-ROI patches. In our experiment, we used the LIBSVM C++ package (version 3.21). The learning conditions were determined on the basis of the training dataset as default parameters. The accuracy of the training was approximately 97.3%.
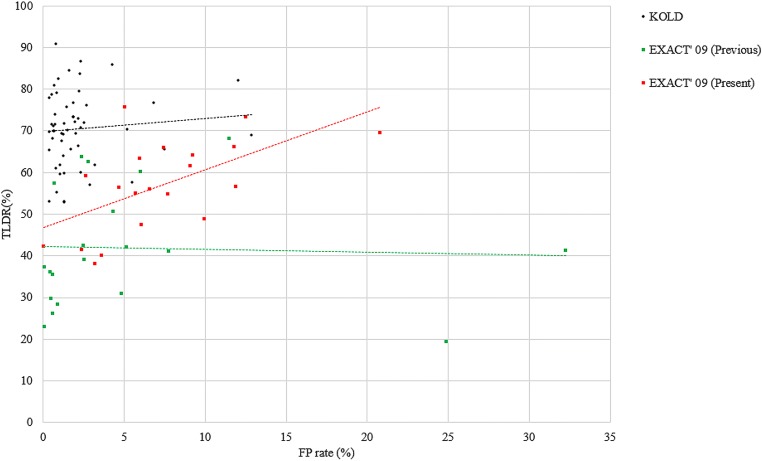
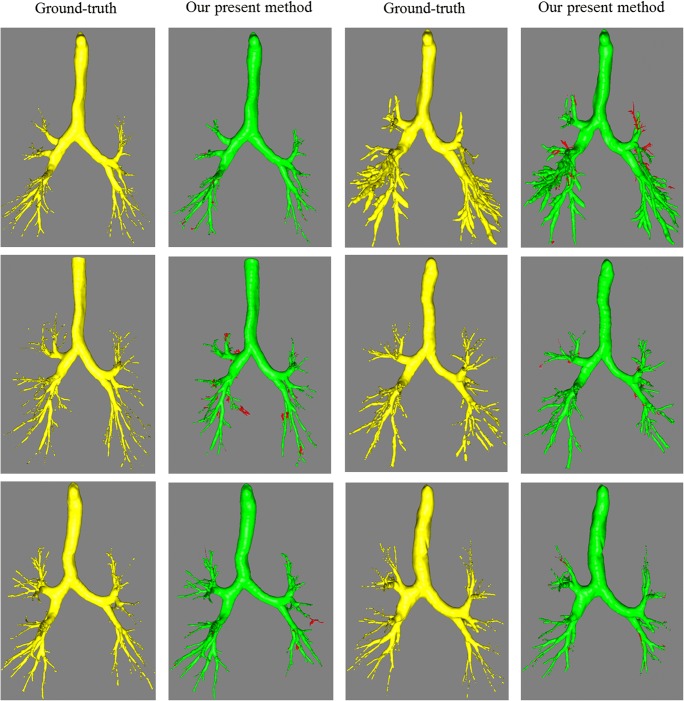
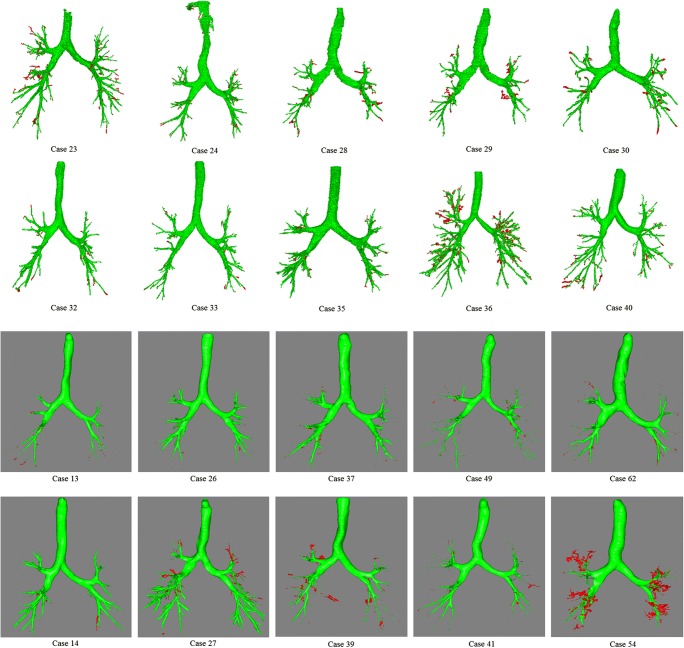
We compared the EXACT′09 results obtained using our proposed method with and without SVM-based ACS and FPR. We also listed the results of our proposed method in KOLD dataset. For evaluation, we computed the tree length (TL) by computing the sum of the length of all correctly detected trees, the tree length detection ratio (TLDR) by computing the fraction of tree length that is detected correctly relative to the ground truth of the airway region, the leakage volume (LV) by calculating the volume of regions that are not marked as “correct” in the ground truth, and the FP rate by calculating the fraction of the total segmented volume that is not marked as “correct” relative to the ground truth [9]. Table 4 shows the overall results, including the average TLDR, average LV, and average FP rate for the previous and current methods. We applied the same evaluation method for the KOLD dataset testing. The previous method was developed using the weighted summation of the multi-scale top-hat transform. The segmentation results, obtained by applying our proposed method to both the 55 KOLD cohort group and EXACT′09 public dataset, have been represented in Fig. 5. Figure 6 represents the visualization results of our proposed method and the ground truth of the KOLD dataset. Figures 8 and 9 represent the segmentation results of 10 cases selected from the KOLD dataset and EXACT′09, respectively. Finally, the computation time of our method for each case is approximately 10–30 min on a system with a quad-core i7 CPU running at 3.4 GHz. The most time-consuming parts were the HEF filtering to select tubular candidate voxels and the SVM classifier for removing FP regions, which were performed for approximately 7–20 min in total. The other procedures, such as multiscale HEF and fuzzy connectedness, also took approximately 3–10 min.
Table 4.
The overall result
| TLDR (%) | LV (mm3) | FP rate (%) | |
|---|---|---|---|
| Previous method (EXACT’ 09) | 41.8 ± 11.0 | 549.9 ± 860.3 | 5.67 ± 9.01 |
| Present method (EXACT’ 09) | 56.9 ± 11.0 | 1633.0 ± 2408.4 | 7.3 ± 4.66 |
| Present method (KOLD) | 70.5 ± 8.98 | 1511.3 ± 1938.9 | 2.19 ± 2.52 |
Fig. 5.
Comparison of segmentation results for airway regions in the 55 KOLD cohort group and EXACT′09 public dataset
Fig. 6.
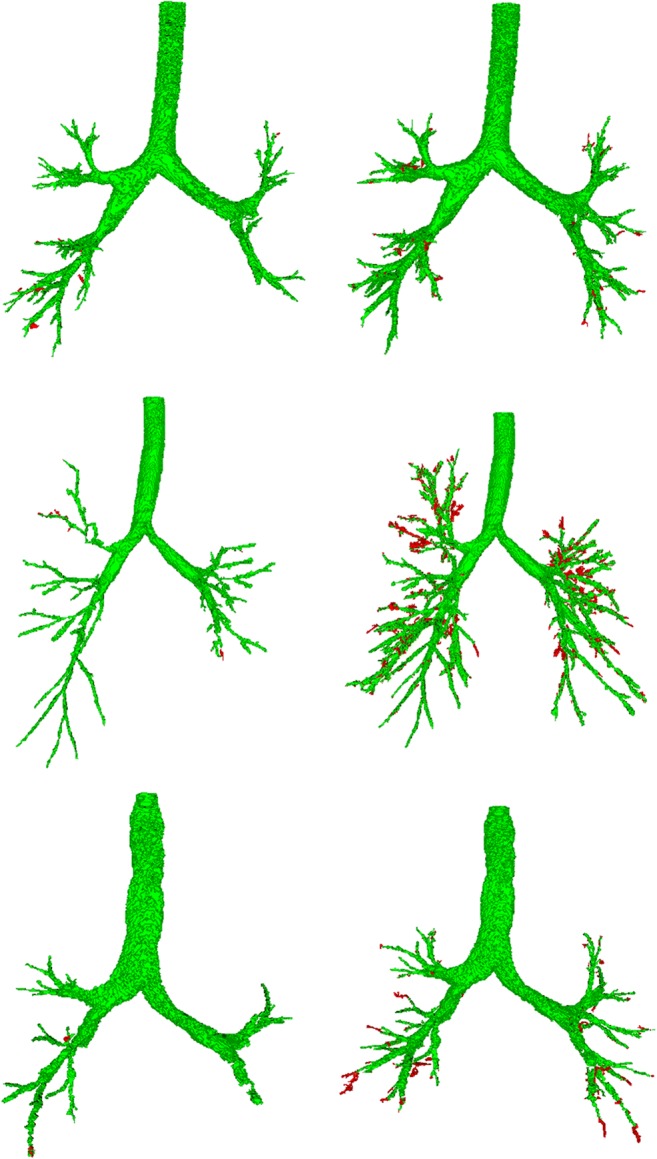
Visual comparison of (a) previous method and (b) current method from EXACT′09 results (green: true positive, red: FP)
Fig. 8.
Visual comparison of the ground truth and final results
Fig. 9.
Visualization of airway segmentation. Top 10 cases (EXACT′09) and bottom 10 cases (KOLD)
Discussion and Conclusion
We proposed a fully automatic approach that segments the airway region from 3D volumetric chest CT scans using hybrid enhancement filtering, the fuzzy connectedness technique, and an SVM classifier. We evaluated the performance of this approach on 75 chest CT volumes. Compared with the other methods, our approach has the following benefits: (1) It does not require tracing the airway tree and thus, and produces less leakage; (2) it uses a combination of not only a tube structure-based filter but also a multiscale structural enhancement filter to better depict the tubular structures with different radii in the 3D volumetric chest CT scans.
Table 5 summarizes the performance comparison of the other methods based on several algorithms [41]. As is evident from the results, our proposed approach could extract smaller airway branches within a little FP region increase. To visually indicate the performance of our method, we plotted the segmentation results obtained using the previously and currently used methods in Fig. 5. It can be seen that the current method can extract a more integrated airway region than that of the previous method. The previous method was unable to clear an integrated airway region; furthermore, it always engendered some leakage to a certain degree. As a reminder, in the previous method, we used multi-scale top-hat transform maps and kernels of various sizes to develop a scheme of adaptively applying weights to enhance small-sized branches that do not correspond to the initial airway and then summarized them. However, the current method improves upon this by removing the FP using the SVM classifier after extracting as many branches as possible, including FPs, by applying Frangi filtering to the top-hat transformation used in the previous method. Compared with the other methods of EXACT′09, our current method was one of the higher performing methods among the EXACT′09 methods in terms of tree-length detection rate. As shown in Fig. 6, our current method can extract more small bronchi branches to form an integrated airway region. In addition, FP regions exist to a certain extent; however, many true negative regions also exist that visually appear as smaller bronchi branches than those in the reference data although they were judged as FP regions.
Table 5.
Comparison of our method and the EXACT’09 methods
| Branch count | Branch detected (%) | Tree length (cm) | Tree length detected (%) | Leakage count | Leakage volume (mm3) | FP rate | |
|---|---|---|---|---|---|---|---|
| CADTB | 91.1 | 43.5 | 64.6 | 36.4 | 2.5 | 152.3 | 1.27 |
| ARTEMIS-TMSP | 157.8 | 62.8 | 122.4 | 55.9 | 12.0 | 563.5 | 1.96 |
| UAVisionLab | 74.2 | 32.1 | 51.9 | 26.9 | 4.2 | 430.4 | 3.63 |
| NagoyaLoopers | 186.8 | 76.5 | 158.7 | 73.3 | 35.5 | 5138.2 | 15.56 |
| DIKU | 150.4 | 59.8 | 118.4 | 54.0 | 1.9 | 18.2 | 0.11 |
| VOLCED | 77.5 | 36.7 | 54.4 | 31.3 | 2.3 | 116.3 | 0.92 |
| TubeLink | 146.8 | 57.9 | 125.2 | 55.2 | 6.5 | 576.6 | 2.44 |
| Sevilla | 71.5 | 30.9 | 52.0 | 26.9 | 0.9 | 126.8 | 1.75 |
| Philips ResearchLab Hamburg | 139.0 | 56.0 | 100.6 | 47.1 | 13.5 | 368.9 | 1.58 |
| VIA | 79.3 | 32.4 | 57.8 | 28.1 | 0.4 | 14.3 | 0.11 |
| ICCAS-VCM | 93.5 | 41.7 | 65.7 | 34.5 | 1.9 | 39.2 | 0.41 |
| yactaTreeTracer | 130.1 | 53.8 | 95.8 | 46.6 | 5.6 | 559.0 | 2.47 |
| GVFTubeSeg | 152.1 | 63.0 | 122.4 | 58.4 | 5.0 | 372.4 | 1.44 |
| WEB2 | 161.4 | 67.2 | 115.4 | 57.0 | 44.1 | 1873.4 | 7.27 |
| Iowa-1 | 148.7 | 63.1 | 119.2 | 58.9 | 10.4 | 158.8 | 1.19 |
| FF_ITC | 198.3 | 79.6 | 177.1 | 79.9 | 115.5 | 2119.6 | 11.92 |
| HybAir | 123.8 | 51.1 | 91.1 | 43.9 | 9.1 | 351.2 | 6.78 |
| Our method | 158.7 | 64.9 | 121.7 | 56.9 | 109.8 | 1633.0 | 7.30 |
Compared with the thresholding technique and region-growing-based method [10–16], our proposed method is more sensitive to the tubular structures in the lung region and does not suffer from leakage. The Frangi filter analysis can detect tubular structures effectively; however, there are several tissues, such as blood vessels in the lung area with similar tubular structures as those in the airway region. To extract the candidate airway region and remove the remaining areas except the airway area, the adaptive multiscale HEF is used in our method. Compared with the original tubular structure-based detection filtering, the adaptive multiscale HEF can detect and extract more candidate small branches with different radii as the multiscale factor. This is possible because the tubular structure is surely enhanced and the enhancement effect of the FP regions is reduced by applying the tubular detection filter that is once again applied to the enhanced tubular structure and the FP regions generated by the top-hat transformation. The comparative results of adaptive multiscale HEF and the tubular structure-based detection filtering method reveal that the adaptive multiscale HEF performs better in extracting both the principle bronchus and small branches with different radii, and it is definitely more feasible than the tubular structure-detection method for acquiring an integrated airway region.
From the results of the Frangi filter analysis and adaptive multiscale HEF, these results cover many airway regions, but running the SVM classifier in this area can take a lot of time. Therefore, we connect the disconnected airway branches by using the fuzzy connectedness technique, which reflects the connection characteristic of intensity for the region that is disconnected or not found in candidate airway region and covers the uncovered region. Thus, running SVM classification selectively using only the connected regions can greatly reduce the computation time and cover the small airway branches of the peripheral region to some extent.
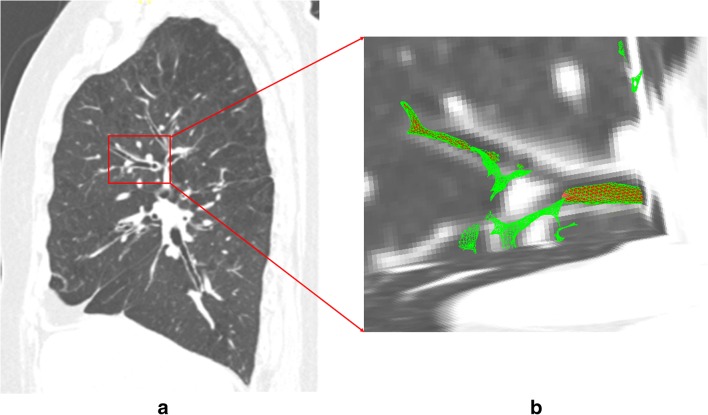
In the final candidate airway region, it can be obviously seen that there are many FP regions around the airway region, especially the small airway branches. The FP regions belong to the surrounding lung parenchyma and the regions under the bifurcation area of pulmonary vessels, which show a locally similar intensity and shape to the airway region. In these FP regions, the density is a little bit lower than the surrounding lung parenchyma regions, which appear to be surrounded by higher-density structures. However, these regions are not exactly the same as the tubular structure region, as shown in Fig. 7. The tube-like structure is the one with low-intensity regions surrounded by higher-intensity regions, as in Fig. 7, and the intensity distribution of the FP region has the structure shown in Fig. 7 with the dark region locally surrounded by the higher-intensity areas. Based on this differential property, using the conventional features, tubular-specific features, and SVM classifier, we can classify the true positive and FP regions.
Fig. 7.
Intensity distribution of true positive and FP regions a CT scan and b rendering view (red: true positive, green: FP)
Our proposed method exhibited a high airway branch detection rate and seems to obtain more undamaged results. Our proposed method can extract various size-based airway branches, but if the candidate airway regions extended by fuzzy connectedness are distributed in lung parenchyma where the intensity difference between that of the airway branch region is small, it can be directed in the wrong direction at the endpoint of the airway branch. If not removed by the SVM classified, this can lead to a large FP region. In Figs. 8 and 9, we can see a red mark of the result figure with an odd direction at the endpoint of airway branches. This phenomenon occurs when the airway is bifurcated or when the intensity becomes higher in a specific area because of sputum or sting. These problems need to be improved in future studies.
We presented a hybrid filtering and SVM classifier-based airway region segmentation framework. A comparison between the results of the presented method and those of other methods from the EXACT′09 data set showed that our method was one of the higher performers. The method limitations are a higher FP rate than that of other methods and a risk of leakage. In future work, we will apply 3D convolutional neural network for the airway region segmentation.
Funding Information
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2016R1C1B1011105) and a grant (2014-7006) from the Asan Institute for Life Sciences, Asan Medical Center, Seoul, Korea.
References
- 1.Porpodis K, et al. Pneumothorax and asthma. J Thorac Dis. 2014;6:S152. doi: 10.3978/j.issn.2072-1439.2014.03.05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kiraly AP, Higgins WE, McLennan G, Hoffman EA, Reinhardt JM. Three-dimensional human airway segmentation methods for clinical virtual bronchoscopy. Acad Radiol. 2002;9:1153–1168. doi: 10.1016/S1076-6332(03)80517-2. [DOI] [PubMed] [Google Scholar]
- 3.Li B, Christensen GE, Hoffman EA, McLennan G, Reinhardt JM. Pulmonary CT image registration and warping for tracking tissue deformation during the respiratory cycle through 3D consistent image registration. Med Phys. 2008;35:5575–5583. doi: 10.1118/1.3005633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen B, Kitasaka T, Honma H, Takabatake H, Mori M, Natori H, Mori K. Automatic segmentation of pulmonary blood vessels and nodules based on local intensity structure analysis and surface propagation in 3D chest CT images. Int J Comput Assist Radiol Surg. 2012;7:465–482. doi: 10.1007/s11548-011-0638-5. [DOI] [PubMed] [Google Scholar]
- 5.Hu S, Hoffman EA, Reinhardt JM. Automatic lung segmentation for accurate quantitation of volumetric X-ray CT images. IEEE Trans Med Imaging. 2001;20:490–498. doi: 10.1109/42.929615. [DOI] [PubMed] [Google Scholar]
- 6.Kuhnigk J-M, Hahn H, Hindennach M, Dicken V, Krass S, Peitgen H-O: Lung lobe segmentation by anatomy-guided 3 D watershed transform. Proc. Proceedings of SPIE: City
- 7.Lee YK, et al. Quantitative assessment of emphysema, air trapping, and airway thickening on computed tomography. Lung. 2008;186:157–165. doi: 10.1007/s00408-008-9071-0. [DOI] [PubMed] [Google Scholar]
- 8.Mori K, et al.: Lung lobe and segmental lobe extraction from 3D chest CT datasets based on figure decomposition and Voronoi division. Proc. Medical Imaging: City
- 9.Lo P, van Ginneken B, Reinhardt JM, Yavarna T, de Jong PA, Irving B, Fetita C, Ortner M, Pinho R, Sijbers J, Feuerstein M, Fabijanska A, Bauer C, Beichel R, Mendoza CS, Wiemker R, Lee J, Reeves AP, Born S, Weinheimer O, van Rikxoort EM, Tschirren J, Mori K, Odry B, Naidich DP, Hartmann I, Hoffman EA, Prokop M, Pedersen JH, de Bruijne M. Extraction of airways from CT (EXACT'09) IEEE Trans Med Imaging. 2012;31:2093–2107. doi: 10.1109/TMI.2012.2209674. [DOI] [PubMed] [Google Scholar]
- 10.Aykac D, Hoffman EA, McLennan G, Reinhardt JM. Segmentation and analysis of the human airway tree from three-dimensional X-ray CT images. IEEE Trans Med Imaging. 2003;22:940–950. doi: 10.1109/TMI.2003.815905. [DOI] [PubMed] [Google Scholar]
- 11.Mori K, Hasegawa J-I, Toriwaki J-I, Anno H, Katada K: Automated extraction and visualization of bronchus from 3D CT images of lung. Proc. Computer Vision, Virtual Reality and Robotics in Medicine: City
- 12.Singh H, Crawford M, Curtin J, Zwiggelaar R: Automated 3D segmentation of the lung airway tree using gain-based region growing approach. Proc. International Conference on Medical Image Computing and Computer-Assisted Intervention: City
- 13.Sonka M, Park W, Hoffman EA. Rule-based detection of intrathoracic airway trees. IEEE Trans Med Imaging. 1996;15:314–326. doi: 10.1109/42.500140. [DOI] [PubMed] [Google Scholar]
- 14.Kitasaka T, Mori K, Hasegawa J, Toriwaki J. A method for extraction of bronchus regions from 3D branch tracing and image sharpening for airway tree chest X-ray images by analyzing structural features of the bronchus. Forma. 2002;17:321–338. [Google Scholar]
- 15.Tschirren J, Hoffman EA, McLennan G, Sonka M. Intrathoracic airway trees: Segmentation and airway morphology analysis from low-dose CT scans. IEEE Trans Med Imaging. 2005;24:1529–1539. doi: 10.1109/TMI.2005.857654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Feuerstein M, Kitasaka T, Mori K: Adaptive branch tracing and image sharpening for airway tree extraction in 3-D chest CT. Proc. Proc Second International Workshop on Pulmonary Image Analysis: City
- 17.Schlathoelter T, Lorenz C, Carlsen IC, Renisch S, Deschamps T: Simultaneous segmentation and tree reconstruction of the airways for virtual bronchoscopy. Proc Medical Imaging 2002: City
- 18.Lo P, Sporring J, Ashraf H, Pedersen JJ, de Bruijne M. Vessel-guided airway tree segmentation: A voxel classification approach. Med Image Anal. 2010;14:527–538. doi: 10.1016/j.media.2010.03.004. [DOI] [PubMed] [Google Scholar]
- 19.Bauer C, Eberlein M, Beichel RR. Graph-based airway tree reconstruction from chest CT scans: evaluation of different features on five cohorts. IEEE Trans Med Imaging. 2015;34:1063–1076. doi: 10.1109/TMI.2014.2374615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lo P, de Bruijne M: Voxel classification based airway tree segmentation. Proc. Medical Imaging: City [DOI] [PubMed]
- 21.Yano H, Marco F, Kitasaka T, Mori K: Study on bronchus region extraction from 3D chest CT images using loca1 intensity structure analysis and CT value distribution feature. The institute of electronics information and communication, MI2009–13:69–74, 2009
- 22.Xu Z, Bagci U, Foster B, Mansoor A, Udupa JK, Mollura DJ. A hybrid method for airway segmentation and automated measurement of bronchial wall thickness on CT. Med Image Anal. 2015;24:1–17. doi: 10.1016/j.media.2015.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Meng Q, Kitasaka T, Nimura Y, Oda M, Ueno J, Mori K: Automatic segmentation of airway tree based on local intensity filter and machine learning technique in 3D chest CT volume. Int J Comput Assist Radiol Surg:1–17, 2016 [DOI] [PubMed]
- 24.Chae EJ, Seo JB, Song JW, Kim N, Park BW, Lee YK, Oh YM, Lee SD, Lim SY. Slope of emphysema index: an objective descriptor of regional heterogeneity of emphysema and an independent determinant of pulmonary function. Am J Roentgenol. 2010;194:W248–W255. doi: 10.2214/AJR.09.2672. [DOI] [PubMed] [Google Scholar]
- 25.Ballard DH. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recogn. 1981;13:111–122. doi: 10.1016/0031-3203(81)90009-1. [DOI] [Google Scholar]
- 26.Frangi AF, Niessen WJ, Vincken KL, Viergever MA: Multiscale vessel enhancement filtering. Proc. International Conference on Medical Image Computing and Computer-Assisted Intervention: City
- 27.Serra J: Image analysis and mathematical morphology, v. 1. Academic press, 1982
- 28.Kong TY, Rosenfeld A: Topological algorithms for digital image processing. Elsevier, 1996
- 29.Kimmel R, Shaked D, Kiryati N, Bruckstein AM: Skeletonization via distance maps and level sets. Proc. Photonics for Industrial Applications: City
- 30.Telea A, Vilanova A: A robust level-set algorithm for centerline extraction. Proc. Proceedings of the symposium on Data visualisation 2003: City
- 31.Udupa JK, Samarasekera S. Fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation. Graph Models Image Process. 1996;58:246–261. doi: 10.1006/gmip.1996.0021. [DOI] [Google Scholar]
- 32.Chang Y, Lim J, Kim N, Seo JB, Lynch DA. A support vector machine classifier reduces interscanner variation in the HRCT classification of regional disease pattern in diffuse lung disease: Comparison to a Bayesian classifier. Med Phys. 2013;40:051912. doi: 10.1118/1.4802214. [DOI] [PubMed] [Google Scholar]
- 33.Chabat F, Yang G-Z, Hansell DM. Obstructive lung diseases: Texture classification for differentiation at ct 1. Radiology. 2003;228:871–877. doi: 10.1148/radiol.2283020505. [DOI] [PubMed] [Google Scholar]
- 34.Kim N, Seo JB, Lee Y, Lee JG, Kim SS, Kang S-H. Development of an automatic classification system for differentiation of obstructive lung disease using HRCT. J Digit Imaging. 2009;22:136–148. doi: 10.1007/s10278-008-9147-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rudyanto RD, Kerkstra S, van Rikxoort EM, Fetita C, Brillet PY, Lefevre C, Xue W, Zhu X, Liang J, Öksüz İ, Ünay D, Kadipaşaogˇlu K, Estépar RSJ, Ross JC, Washko GR, Prieto JC, Hoyos MH, Orkisz M, Meine H, Hüllebrand M, Stöcker C, Mir FL, Naranjo V, Villanueva E, Staring M, Xiao C, Stoel BC, Fabijanska A, Smistad E, Elster AC, Lindseth F, Foruzan AH, Kiros R, Popuri K, Cobzas D, Jimenez-Carretero D, Santos A, Ledesma-Carbayo MJ, Helmberger M, Urschler M, Pienn M, Bosboom DGH, Campo A, Prokop M, de Jong PA, Ortiz-de-Solorzano C, Muñoz-Barrutia A, van Ginneken B. Comparing algorithms for automated vessel segmentation in computed tomography scans of the lung: the VESSEL12 study. Med Image Anal. 2014;18:1217–1232. doi: 10.1016/j.media.2014.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xiao C, Staring M, Shamonin D, Reiber JH, Stolk J, Stoel BC. A strain energy filter for 3D vessel enhancement with application to pulmonary CT images. Med Image Anal. 2011;15:112–124. doi: 10.1016/j.media.2010.08.003. [DOI] [PubMed] [Google Scholar]
- 37.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20:273–297. [Google Scholar]
- 38.Keshani M, Azimifar Z, Tajeripour F, Boostani R. Lung nodule segmentation and recognition using SVM classifier and active contour modeling: a complete intelligent system. Comput Biol Med. 2013;43:287–300. doi: 10.1016/j.compbiomed.2012.12.004. [DOI] [PubMed] [Google Scholar]
- 39.Smola AJ, Schölkopf B: Learning with kernels: Citeseer, 1998
- 40.Zheng S, Liu J, Tian JW. A new efficient SVM-based edge detection method. Pattern Recogn Lett. 2004;25:1143–1154. doi: 10.1016/j.patrec.2004.03.009. [DOI] [Google Scholar]