Abstract
Malignant breast tumors and benign masses appear in mammograms with different shape characteristics: the former usually have rough, spiculated, or microlobulated contours, whereas the latter commonly have smooth, round, oval, or macrolobulated contours. Features that characterize shape roughness and complexity can assist in distinguishing between malignant tumors and benign masses. Signatures of contours may be used to analyze their shapes. We propose to use a signature based on the turning angle function of contours of breast masses to derive features that capture the characteristics of shape roughness as described above. We propose methods to derive an index of the presence of convex regions (XRTA), an index of the presence of concave regions (VRTA), an index of convexity (CXTA), and two measures of fractal dimension (FDTA and FDdTA) from the turning angle function. The methods were tested with a set of 111 contours of 65 benign masses and 46 malignant tumors with different parameters. The best classification accuracies in discriminating between benign masses and malignant tumors, obtained for XRTA, VRTA, CXTA, FDTA, and FDdTA in terms of the area under the receiver operating characteristics curve, were 0.92, 0.92, 0.93, 0.93, and, 0.92, respectively.
Key words: Breast cancer, tumor classification, fractal dimension, index of convexity, index of concavity, shape features, turning angle function
ANALYSIS OF CONTOURS AND SIGNATURES
Shape Analysis of Breast Tumors
Breast tumors and masses appear in mammograms with different shape characteristics: malignant tumors usually have rough, spiculated, or microlobulated contours, whereas benign masses commonly have smooth, round, oval, or macrolobulated contours.1,2 Measures that can quantitatively represent shape roughness and complexity can assist in the classification of malignant tumors and benign masses.3,4 Objective features of shape complexity such as compactness, fractional concavity (Fcc), spiculation index (SI), a Fourier-descriptor-based factor (FF), fractal dimension (FD), moments, chord-length statistics, and wavelet transform modulus-maxima have been developed to distinguish benign masses from malignant tumors using pattern recognition methods for computer-aided diagnosis (CADx) of breast cancer.3–10
However, atypical cases of macrolobulated or spiculated benign masses, as well as microlobulated or well-circumscribed malignant tumors, create difficulties in pattern classification.3,4 Regardless, in comparative analysis of several features of shape, edge-sharpness, and texture for the classification of breast masses and tumors, shape factors such as Fcc, FF, and SI have been observed to lead to higher classification accuracies than measures related to texture and density variation.5,7,11
Notwithstanding the relative success of measures of shape in the classification of breast tumors and masses, obtaining precise and artifact-free boundaries of masses from mammograms remains to be a difficult problem.7,12,13 Computer-detected contours may be expected to contain inaccuracies and artifacts due to the limitations of the procedures for the detection and segmentation of masses in mammograms; contours of masses drawn manually on mammograms by radiologists may contain noise related to hand tremor.
In this work, we propose a novel approach to obtain signatures of contours based on the turning angle function that takes into account reduction of noise and artifacts. We also propose the development of methods based on the signature to extract shape descriptors with the aim of classifying the contours of breast masses and tumors.14 Different from our previous work15 where the turning angle function was used to derive a polygonal model of a given contour, the signature of the contour being proposed in the present work, while retaining relevant characteristics of the contour, does not facilitate the derivation of a polygonal model of the original contour. In other related works,16,17 we have proposed a different procedure to derive a polygonal model of a given contour that preserves spicules and details of diagnostic importance. We have also proposed a method to derive a spiculation index from the turning angle function obtained from a polygonal model of a given contour.16,17 In the present work, we present new methods to derive shape factors that represent the presence of convex and concave regions in the contour, to compute an index of convexity, and to estimate the fractal dimension obtained from the signature derived from the turning angle function of the original contour.
To evaluate the performance of the proposed shape descriptors in terms of the efficiency in the classification of breast masses, we compare the results with those provided by fractional concavity (Fcc) using the method of Rangayyan et al.4 and FD as obtained by Rangayyan and Nguyen8 in terms of the area Az under the receiver operating characteristics (ROC) curve.
Signatures of Contours
Signatures of contours may be used to analyze their shapes. The most commonly used method to transform a two-dimensional (2D) contour into a one-dimensional (1D) signature is in terms of the radial distance from each contour point to the centroid of the contour expressed as a function of the index of the contour point. Given a contour with N points {x(n), y(n)}, n = 1,2,...,N, the signature Sd(n) is defined as 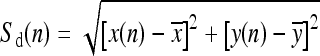 . Here,
. Here, 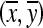 is the centroid of the contour, with the coordinates given by the averages of the corresponding coordinates of all of the contour points. A benign mass that is round or macrolobulated will have a smooth signature; on the contrary, a malignant tumor that is spiculated or microlobulated will have a rough and jagged signature.18 The 1D signature of a contour as above may be used to derive the fractal dimension (FD) to represent the complexity of the contour.8
is the centroid of the contour, with the coordinates given by the averages of the corresponding coordinates of all of the contour points. A benign mass that is round or macrolobulated will have a smooth signature; on the contrary, a malignant tumor that is spiculated or microlobulated will have a rough and jagged signature.18 The 1D signature of a contour as above may be used to derive the fractal dimension (FD) to represent the complexity of the contour.8
Another type of signature Sd(n) may be defined as the complex number 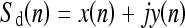 where
where 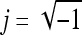 . Fourier descriptors and normalized shape factors to characterize roughness may be derived from Sd(n).3,18
. Fourier descriptors and normalized shape factors to characterize roughness may be derived from Sd(n).3,18
Pohlman et al.19 defined the signature of a given contour of a breast mass as the radial distance to the contour from its centroid expressed as a function of the angle of the radial line in the interval (0°, 360°). Such a function could be multivalued for an irregular or spiculated contour. The signature computed in this manner would also be undefined, in certain ranges of the angle, for a contour for which the centroid falls outside the region enclosed by the contour.
A major advantage with the use of 1D signatures is the reduction in dimensionality from the corresponding 2D contours. Signatures may be filtered or processed for the reduction of noise and artifacts in the contour. Furthermore, shape factors may be derived more easily from 1D signatures than from the corresponding 2D contours.
THE TURNING ANGLE FUNCTION
The turning angle function TC(Sn) of the contour C is the cumulative function of turning angles and may be obtained by deriving the counterclockwise angle between the tangent at the segment sn and the x-axis and expressing it as a function of the arc length of Sn. The turning angle function is also known as the tangent function and has been used as a signature to represent the shape of a given contour (or its polygonal model) and used in applications related to shape retrieval20–27. The turning angle function keeps track of the turning angle of the contour, increasing with convex regions and decreasing with concave regions. The turning angle of a segment Si is the difference or step between TC(Si + 1) and TC(Si). The turning angle ranges in the interval (−180°, 180°). Negative values represent concave regions and positive values represent convex regions. For a convex contour, TC(Sn) is a monotonic function, starting at some value φ and increasing to φ + 2π. For a non-convex polygon, TC(Sn) can become arbitrarily large, as it accumulates the total amount of turning angles, obeying the range of 2π between the starting point and the final point.27
Figures 1 and 2 show the turning angle functions of the contours of a benign mass and a malignant tumor, respectively. It is evident that the turning angle function of the malignant tumor is more complex and rough than that of the benign mass. However, the turning angle functions include noise due to artifacts in the contours and need to be filtered before further analysis.
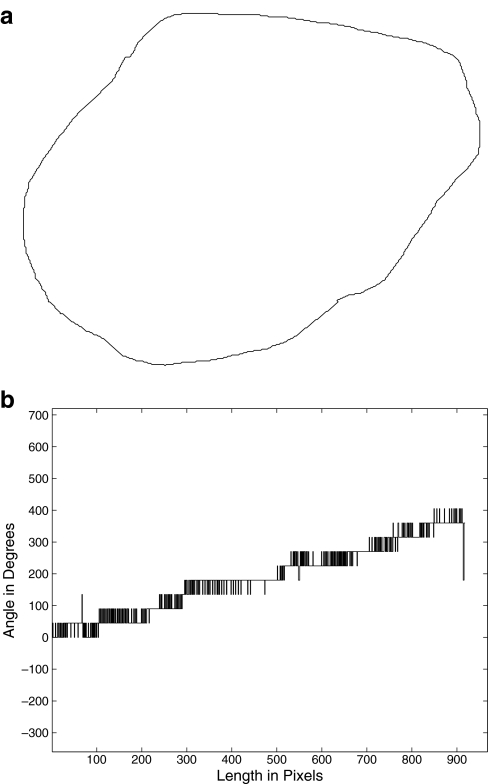
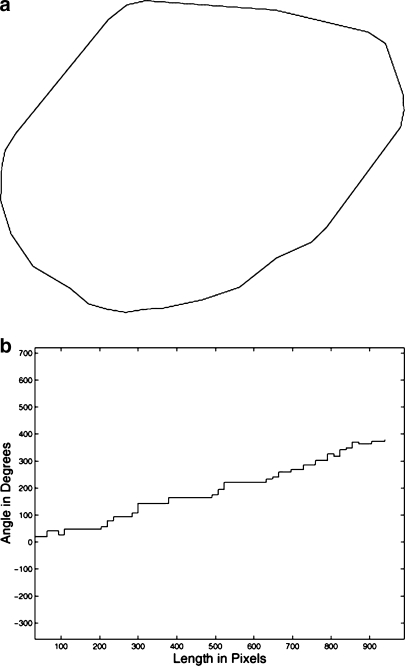
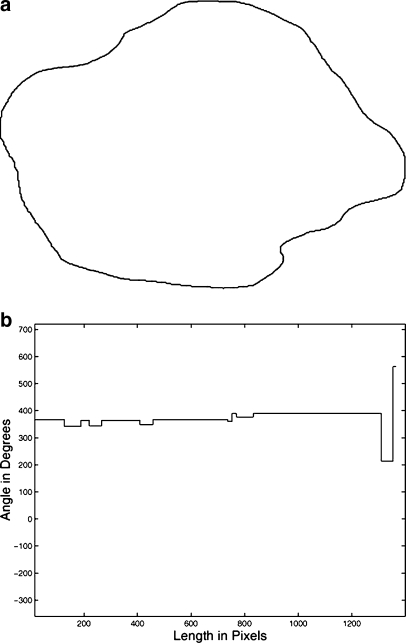
Fig 1.
a A manually drawn contour of a benign mass with a relatively smooth and convex contour with 916 points (pixels) and resolution of 50 μm per pixel. b Turning angle function of the contour with TC(Sl) = 0° and TC(S916) = 360°.
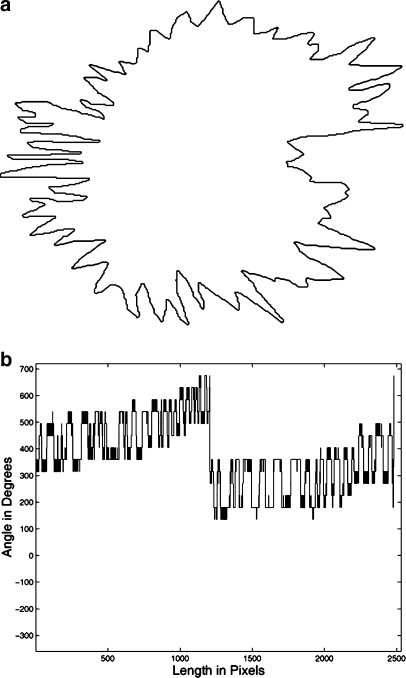
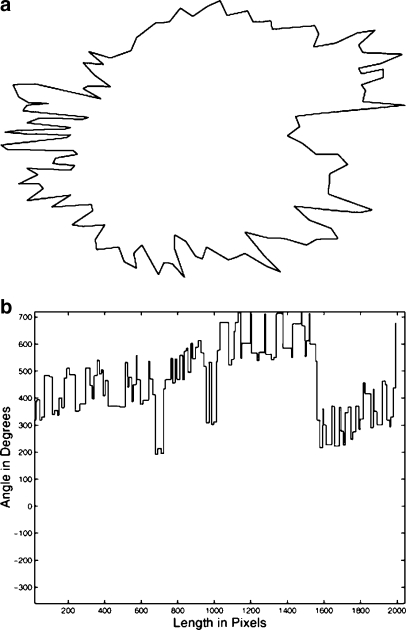
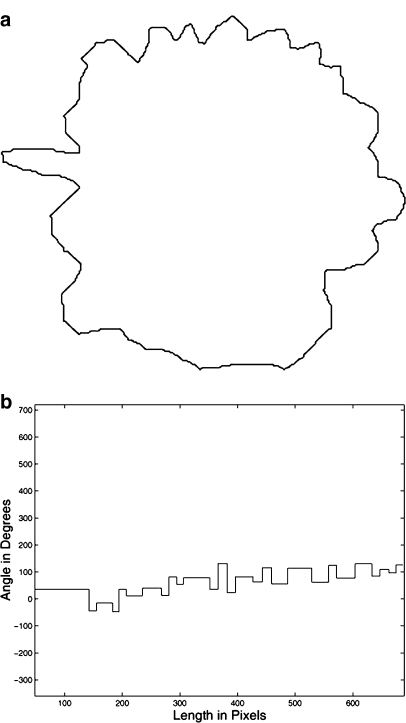
Fig 2.
a A manually drawn contour of a malignant tumor with a spiculated contour including concave and convex segments with 2,478 points (pixels) and resolution of 50 μm per pixel. b Turning angle function of the contour with TC(Sl) = 315° and TC(S2478) = 675°.
SIGNATURE BASED ON THE TURNING ANGLE FUNCTION
Figures 1b and 2b illustrate the turning angle functions of the contours of a benign mass and a malignant tumor, respectively. It is readily seen that while the former is a nearly monotonically increasing function (except for the effects of noise or minor variations), the latter has many decreasing and increasing segments related to the concave and convex regions present in the contour of the tumor. The examples indicate that the turning angle function may be used to represent the complexity as well as the variations present in the shapes of breast masses and tumors.
However, computer-detected contours and hand-drawn contours, such as those shown in Figures 1a and 2a, could contain artifacts and noise related to hand tremor and other limitations. As a consequence, the turning angle function could be expected to contain several small segments that are insignificant in the representation of the contours for further analysis, as highlighted in Figure 3. For this reason, we propose to filter the turning angle function in a selective manner so as to remove the artifacts and noise while preserving the significant details.14 The proposed filtering procedure is an iterative process controlled by the size of the segments and the turning angle between adjacent segments. Two rules are applied to every linear segment Si identified from the turning angle function in each iteration:
if the current segment Si and the next segment Si + 1 are both shorter than a threshold Smin, then join Si and Si + 1. The length of the combined segment is equal to the length of the straight line connecting the starting point of Si and the ending point of Si + 1 in the original contour domain. The turning angle of the combined segment is derived as described in Section 2.
if the length of Si or Si + 1 is greater than the threshold Smin, then analyze the turning angle between Si and Si + 1: if (180° − abs(TC(Si + 1) − TC(Si))) ≥ θmax, then join Si and Si + 1; else retain Si and Si + 1. The procedure for joining two segments is described under Rule 1.
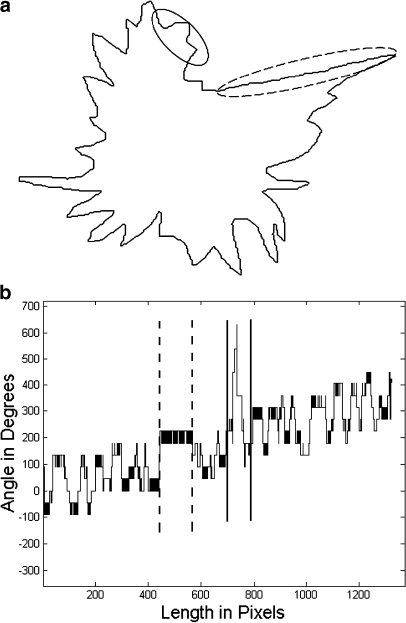
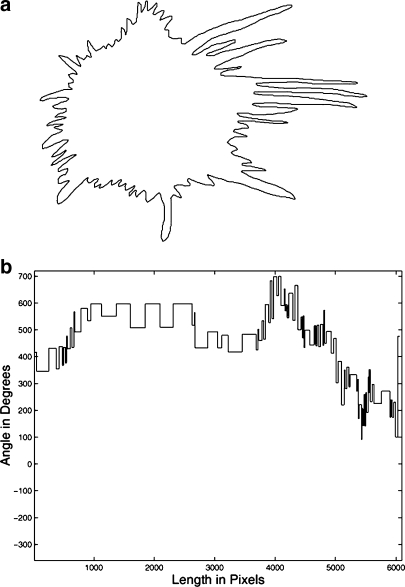
Fig 3.
A manually drawn contour of a malignant tumor: a Adjacent segments within the dashed ellipse possess high internal angles and are small (caused by hand tremor or other limitations). Some adjacent segments within the solid ellipse present relevant internal angles. b The respective artifacts of the highlighted regions on the contour represented in the turning angle function. The region inside the dashed ellipse is represented in the turning angle function as the region between the dashed lines with a sequence of small segments with different directions. The region inside the solid ellipse is represented in the turning angle function as a sequence of segments of different sizes with large changes in direction.
The threshold Smin represents the relevance of a segment and θmax indicates the relevance of the turning angle between two adjacent segments of the contour being analyzed. The relevance of the segment is related to the resolution of the image and the requirements of the application. A high value for θmax means that when the internal angle between two adjacent segments is large, then the segments should be joined. The procedure stops when no segments are joined in an iteration. Figure 4 illustrates the filtering procedure applied to the turning angle function in Figure 3. Note that small segments with no relevant angles have been joined, resulting in a smoother turning angle function. Figures 5 and 6 illustrate the filtered versions of the turning angle functions and the contours corresponding to those in Figures 1 and 2, with Smin = 10 pixels (equivalent to 0.5 mm according to the image resolution) and θmax = 170°. The filtered turning angle function maintains all the relevant information to reconstruct a polygonal model of a given contour.14,15 The resulting polygonal model is free of major artifacts and noise, while preserving important spicules and lobules in the given contour.
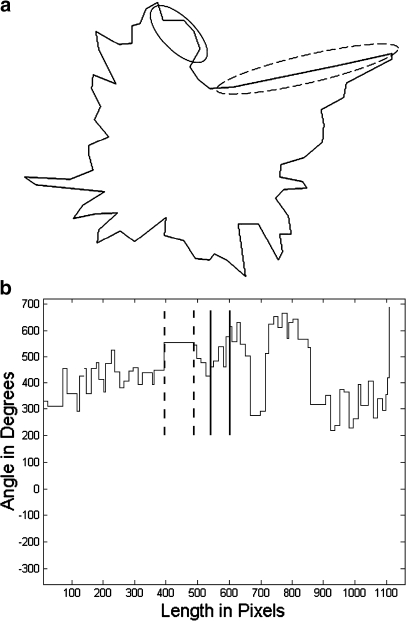
Fig 4.
a Filtered version of the contour in Figure 3a with reduction of artifacts. b Filtered version of the turning angle function in Figure 3b with Smin = 10 pixels and θmax = 170°.
Fig. 5.
a Filtered version of the contour in Figure 1a with reduction of artifacts. b Filtered version of the turning angle function in Figure 1b with Smin = 10 pixels and θmax = 170°.
Fig 6.
a Filtered version of the contour in Figure 2a with reduction of artifacts. b Filtered version of the turning angle function in Figure 2b with Smin = 10 pixels and θmax = 170°.
Although the filtered turning angle function preserves only the significant angles and segments of the original contour, the successive increasing or decreasing sections (see Figs. 5 and 6) do not give any extra information to derive shape factors related to the complexity of the contour, such as fractal dimension and index of convexity. For this reason, we propose to further smooth the filtered turning angle function with the aim of retaining information only about the presence of concave and convex regions in the original contour.
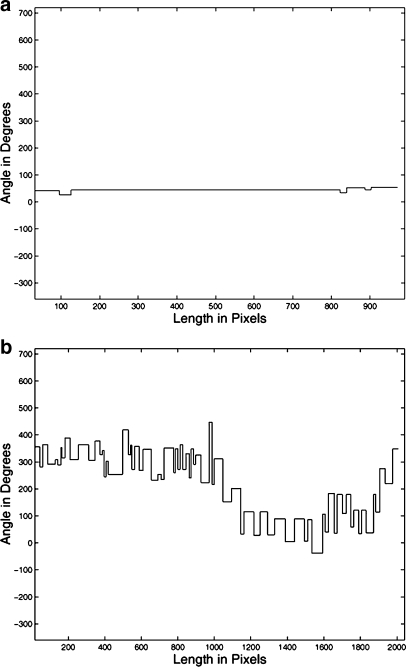
The smoothed filtered turning angle function, which will be referred to in the rest of this paper as the signature based on the turning angle function (or STAF for short), is obtained by replacing each monotonically increasing or decreasing section of the filtered turning angle function by a representative segment and its corresponding turning angle. The new segment length is obtained by summing all related individual segment lengths in the increasing or decreasing section, and the new turning angle is obtained by computing the average of the relative turning angles of the corresponding segments. The STAFs of the benign mass in Figure 1 and the malignant tumor in Figure 2 are shown in Figure 7. Note that the STAF of a nearly convex contour is almost constant, as illustrated in Figure 7a; on the other hand, the STAF of a contour with concavities possesses several variations, as shown in Figure 7b. The STAF, as computed above, does not permit the reconstruction of the original contour or any filtered version thereof.
Fig 7.
Signatures based on the turning angle function with Smin = 10 pixels and θmax = 170° of: a The benign mass with a nearly convex contour shown in Figure 1; b The malignant tumor with a spiculated contour shown in Figure 2. See also Figures 5 and 6.
FEATURE EXTRACTION FROM THE STAF
In this section, we present a set of feature descriptors derived from the STAF of the given contour. The proposed feature descriptors include two different measures of fractal dimension, indices that represent the presence of concave and convex regions in the contour, and an index of convexity.
Fractal Dimension
Fractal analysis may be used to study the complexity and roughness of 1D functions, 2D contours, and images.8,28–33 Fractal analysis may be applied to classify breast masses based on the complexity of their contours.8 Matsubara et al.34 obtained 100% accuracy in the classification of 13 breast masses using FD. The method required the computation of a series of FD values for several contours of a given mass obtained by thresholding the mass at many levels; the variation in FD was used to categorize a given mass as benign or malignant. Pohlman et al.19 obtained a classification accuracy of more than 80% with fractal analysis of signatures of contours of masses based on the radial distance as described in Section 1.2. Rangayyan and Nguyen8 estimated the FD of a set of 111 contours of breast masses and tumors using the ruler and the box-counting methods applied to the 2D contours as well as their 1D signatures [Sd(n) as described in Sect. 1.2]. The best classification performance with Az = 0.89 was obtained with the ruler method applied to the 1D signatures of the contours.
In the present work, the ruler method is applied to the STAFs of the contours of breast masses (referred to as FDTA) and to the first derivatives of the STAF (FDdTA). See Rangayyan and Nguyen8 for details on the ruler method. Each STAF is normalized along both axes to the interval [0,1]. The slope of the curve log(r) vs log(N*r), that is, the log of the size of the ruler (r) vs the log of the number of rulers (N) times the ruler size, is obtained as an estimate of FDTA or FDdTA.
Index of the Presence of Concave Regions and Index of the Presence of Convex Regions
A study of the presence of concave or convex regions may be used to characterize a given contour according to relevant changes in the direction. Related features may be used to classify contours of breast masses as benign or malignant.2,4 Such information could be used to discriminate between lobulated or spiculated contours and relatively smooth or convex contours. To characterize the roughness of a contour, we propose the indices VRTA and XRTA to measure the presence of concave regions and convex regions in a given contour, respectively. Both indices are normalized to the interval [0,1].
VRTA is defined as
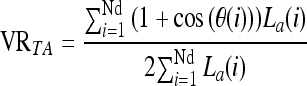 |
1 |
where La(i) is the sum of the lengths of two adjacent segments Si and Si + 1, joined by a drop in the turning angle θ(i), obtained from the STAF, and Nd is the number of drops in angle in the STAF. For a convex contour, the value for VRTA is equal to zero.
XRTA is defined as
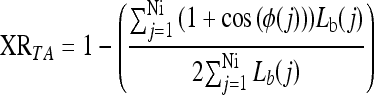 |
2 |
where Lb(j) is the sum of the lengths of two adjacent segments Sj and Sj + 1, joined by an increase in the turning angle ϕ(j), obtained from the STAF, and Ni is the number of steps with increasing angles in the STAF. For a convex contour, the value for XRTA is equal to 1.
Index of Convexity
The index of convexity CXTA combines information regarding the presence of concave regions and convex regions in the contour.
CXTA is defined as
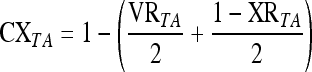 |
3 |
CXTA is normalized to the interval [0,1]. For a convex contour, the value for CXTA is equal to 1. The index decreases as the presence of concave regions increases.
DATA USED: CONTOURS OF BREAST MASSES
Mammograms of 20 cases were obtained from Screen Test: the Alberta Program for the Early Detection of Breast Cancer.5,35,36 The mammograms were digitized using the Lumiscan 85 scanner at a resolution of 50 μm with 12 b/pixel. Fifty-seven regions of interest, of which 37 are related to benign masses and 20 are related to malignant tumors, were obtained.5 The sizes of the benign masses vary in the range 39–437 mm2, with an average of 163 mm2 and a standard deviation of 87 mm2. The sizes of the malignant tumors vary in the range 34–1,122 mm2, with an average of 265 mm2 and a standard deviation of 283 mm2. Most of the benign masses in this dataset are smooth or macrolobulated, whereas most of the malignant tumors are spiculated or microlobulated.
Mammograms containing masses were also obtained from the Mammographic Image Analysis Society (MIAS, UK) database37,38 and the teaching library of the Foothills Hospital (Calgary)3,4. The MIAS images were digitized at a resolution of 50 μm with 8 b/pixel. The Foothills Hospital images were digitized at 62 μm per pixel with 8 b/pixel. This set includes 28 benign masses and 26 malignant tumors with smooth, lobulated, and spiculated contours in both the benign and malignant categories. The sizes of the benign masses vary in the range 32–1,207 mm2, with an average of 281 mm2 and a standard deviation of 288 mm2. The sizes of the malignant tumors vary in the range 46–1,244 mm2, with an average of 286 mm2 and a standard deviation of 292 mm2.
Contours of the masses in the images described above were drawn by an expert radiologist specialized in mammography. The combined dataset used in the present study include 111 contours, with typical and atypical shapes of 65 benign masses and 46 malignant tumors. The diagnostic classification was based upon biopsy (the present work employs the same dataset as that used by Rangayyan and Nguyen8).
RESULTS AND DISCUSSION
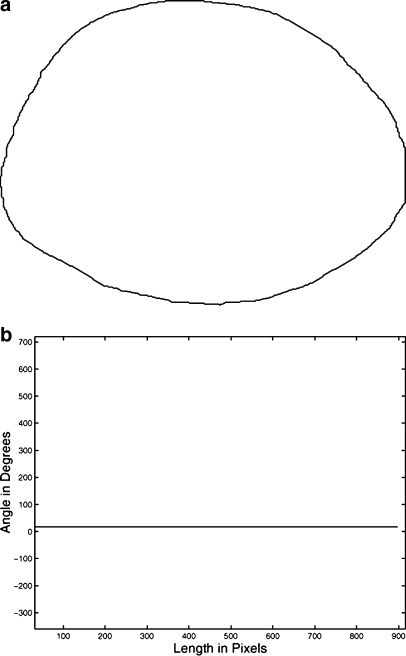
The methods were tested with a set of 111 contours of breast masses; see Section 5 for details regarding the dataset used. Figures 8, 9, 10 and 11 present a set of contours of breast masses and tumors with different shapes, and the respective STAF with Smin = 10 pixels and θmax = 170°. It is worth noting that a convex contour, as shown in Figure 8a, possesses a STAF represented by a constant, resulting in a value equal to zero for FDTA, FDdTA, and VRTA, and a value equal to 1 for XRTA and CXTA.
Fig 8.
a A manually drawn contour of a circumscribed benign mass. FDTA = 0.0, FDTA = 0.0, VRTA = 0.0, XRTA = 1.0, and CXTA = 1.0. b The signature based on the turning angle function with Smin = 10 pixels and θmax = 170°.
Fig 9.
a A manually drawn contour of a macrolobulated malignant tumor. FDTA = 0.14, FDdTA = 0.11, VRTA = 0.45, XRTA = 0.98, and CXTA = 0.76. b The signature based on the turning angle function with Smin = 10 pixels and θmax = 170°.
Fig 10.
a A manually drawn contour of a microlobulated malignant tumor. FDTA = 0.32, FDdTA = 0.30, VRTA = 0.24, XRTA = 0.78, and CXTA = 0.77. b The signature based on the turning angle function with Smin = 10 pixels and θmax = 170°.
Fig 11.
a A manually drawn contour of a spiculated malignant tumor. FDTA = 0.61, FDdTA = 0.57, VRTA = 0.42, XRTA = 0.64, and CXTA = 0.61. b The signature based on the turning angle function with Smin = 10 pixels and θmax = 170°.
To evaluate the proposed methods, the STAF of the 111 contours in the dataset were obtained with several sets of parameters. The shape descriptors VRTA, XRTA, CXTA, FDTA, and FDdTA were derived for each STAF. A sliding threshold was applied to each feature descriptor directly to classify the corresponding mass as benign or malignant. This classification strategy was used because in each experiment, each contour is represented by only one feature; consequently, the classifier does not require any training step. The diagnosis of each mass, as provided by biopsy, was used to validate the classification. The true-positive fraction (TPF) and false-positive fraction (FPF) were computed for each threshold using the results for all of the 111 contours. To evaluate the classification performance of each feature, an ROC curve39 was generated for each experiment, with the sensitivity given by the TPF and the specificity given as 1-FPF.
To evaluate the impact of the choice of Smin on the final results, we tested the features with three different values of Smin (5, 10, and 20 pixels), with θmax set at 170°. The area Az under the ROC curve was computed for each case to serve as a measure of the classification performance of the corresponding feature, as summarized in Table 1. Note that when the indices are applied to characterize contours of lesions in mammograms, with the pixel resolution being 50 or 62 μm, the best results were obtained with Smin set at 10 pixels, which is equivalent to 0.5 or 0.6 mm. The parameters need to be adjusted according to the requirements of the application. Because the performance of the classifier changes when different parameters are used in deriving the polygonal models, we analyzed the statistical significance of the difference between the features for each set of feature descriptors. Considering the parameter Smin = 10 pixels as the reference, the results obtained using FDdTA with all the different combinations of the parameters and FDTA and VRTA with Smin = 20 pixels do not present differences that are statistically significant with p ≤ 0.05.
Table 1.
Comparison of the Classification Performance of the Proposed Indices with Different Values for Smin, and θmax set at 170°
| Method | AZ |
|---|---|
| Fcc from Rangayyan and Nguyen8 | 0.88 |
| FD from Rangayyan and Nguyen8 | 0.89 |
| Compactness from Rangayyan and Nguyen8 | 0.87 |
| Fourier factor from Rangayyan and Nguyen8 | 0.77 |
| FDTA | |
| Smin = 5 pixels | 0.86 |
| Smin = 10 pixels | 0.93 |
| Smin = 20 pixels | 0.91 |
| FDdTA | |
| Smin = 5 pixels | 0.86 |
| Smin = 10 pixels | 0.92 |
| Smin = 20 pixels | 0.91 |
| VRTA | |
| Smin = 5 pixels | 0.87 |
| Smin = 10 pixels | 0.92 |
| Smin = 20 pixels | 0.90 |
| XRTA | |
| Smin = 5 pixels | 0.88 |
| Smin = 10 pixels | 0.92 |
| Smin = 20 pixels | 0.91 |
| CXTA | |
| Smin = 5 pixels | 0.89 |
| Smin = 10 pixels | 0.93 |
| Smin = 20 pixels | 0.92 |
AZ Area under the ROC curve
To compare the performance of the results obtained with the proposed features with the results of other features, we computed the Az value for the shape factor Fcc4 as well as FD obtained using the ruler method applied to 1D signatures of contours as reported by Rangayyan and Nguyen.8 The results are also shown in Table 1. The table also lists, for comparison, the Az values for a spiculation index, compactness, and a Fourier-descriptor-based shape factors as obtained by Rangayyan and Nguyen.8 It is seen that the shape features proposed in the present paper have provided the best results. Further studies are required to evaluate the classification performance of various combinations of the shape features proposed in the present work and previous related works.
The shape factors proposed in this work could also be used to classify breast masses and tumors in terms of margins that are circumscribed, macrolobulated, microlobulated, or spiculated. Such categorization could assist in the preparation of reports in accordance with the terminology used in BI-RADS.2 Further work is in progress to derive fuzzy rules to classify breast mass using various combinations of the proposed shape factors.
CONCLUSION
We have proposed methods to obtain shape features from signatures based on filtered turning angle functions of contours. The features have been shown to be useful in the analysis of contours of breast masses and tumors because of their ability to capture diagnostically important details of shape related to spicules and lobulations. The proposed features have provided high classification accuracies in discriminating between benign breast masses and malignant tumors. The methods should be useful in computer-aided diagnosis of breast cancer.
Acknowledgment
This work was supported by the Conselho Nacional Desenvolvimento Científıco e Tecnológico of Brazil, and the Catalyst Program of Research Services, University of Calgary. We thank Fábio José Ayres, University of Calgary for assistance with the ROC procedures.
References
- 1.Homer MJ. Mammographic Interpretation: A Practical Approach. 2. Boston, MA: McGraw-Hill; 1997. [Google Scholar]
- 2.Breast Imaging Reporting and Data System BI-RADS. 4. Reston, VA: American College of Radiology; 2004. [Google Scholar]
- 3.Rangayyan RM, El-Faramawy NM, Desautels JEL, Alim OA. Measures of acutance and shape for classification of breast tumors. IEEE Trans Med Imaging. 1997;16(6):799–810. doi: 10.1109/42.650876. [DOI] [PubMed] [Google Scholar]
- 4.Rangayyan RM, Mudigonda NR, Desautels JEL. Boundary modelling and shape analysis methods for classification of mammographic masses. Med Biol Eng Comput. 2000;38:487–496. doi: 10.1007/BF02345742. [DOI] [PubMed] [Google Scholar]
- 5.Alto H, Rangayyan RM, Desautels JEL: Content-based retrieval and analysis of mammographic masses. J Electron Imaging 14(2):023016:1–17, 2005
- 6.Bruce LM, Adhami RR. Classifying mammographic mass shapes using the wavelet transform modulus-maxima method. IEEE Trans Med Imaging. 1999;18(12):1170–1177. doi: 10.1109/42.819326. [DOI] [PubMed] [Google Scholar]
- 7.Sahiner BS, Chan HP, Petrick N, Helvie MA, Hadjiiski LM. Improvement of mammographic mass characterization using spiculation measures and morphological features. Med Phys. 2001;28(7):1455–1465. doi: 10.1118/1.1381548. [DOI] [PubMed] [Google Scholar]
- 8.Rangayyan RM, Nguyen TM: Fractal analysis of contours of breast masses in mammograms. J Digital Imaging, 2007, in press 10.1007/s10278-006-0860-9 [DOI] [PMC free article] [PubMed]
- 9.Huo Z, Giger ML, Vyborny CJ, Wolverton DE, Metz CE. Computerized classification of benign and malignant masses on digitized mammograms: A study of robustness. Acad Radiol. 2000;7(12):1077–1084. doi: 10.1016/S1076-6332(00)80060-4. [DOI] [PubMed] [Google Scholar]
- 10.Huo Z, Giger ML, Vyborny CJ. Computerized analysis of multiple-mammographic views: Potential usefulness of special view mammograms in computer-aided diagnosis. IEEE Trans Med Imaging. 2001;20(12):1285–1292. doi: 10.1109/42.974923. [DOI] [PubMed] [Google Scholar]
- 11.Nandi RJ, Nandi AK, Rangayyan RM, Scutt D. Classification of breast masses in mammograms using genetic programming and feature selection. Med Biol Eng Comput. 2006;44(8):683–694. doi: 10.1007/s11517-006-0077-6. [DOI] [PubMed] [Google Scholar]
- 12.Mudigonda NR, Rangayyan RM, Desautels JEL. Detection of breast masses in mammograms by density slicing and texture flow-field analysis. IEEE Trans Med Imaging. 2001;20(12):1215–1227. doi: 10.1109/42.974917. [DOI] [PubMed] [Google Scholar]
- 13.Wei D, Chan HP, Helvie MA, Sahiner B, Petrick N, Adler DD, Goodsitt MM. Classification of mass and normal breast tissue on digital mammograms: multiresolution texture analysis. Med Phys. 1995;22(9):1501–1513. doi: 10.1118/1.597418. [DOI] [PubMed] [Google Scholar]
- 14.Rangayyan RM, Guliato D, Carvalho JD, Santiago SA: Feature extraction from the turning angle function for the classification of breast tumors. In Proceedings of the International Special Topics Conference on Information Technology in Biomedicine -IEEE ITAB2006, Ioannina, Greece, October 2006, 6 pages on CDROM
- 15.Carvalho JD, Rangayyan RM, Guliato D, Santiago SA: Polygonal modeling of contours using the turning angle function. 20th IEEE Canadian Conference on Electrical and Computer Engineering, Vancouver, BC, April 2007, 4 pages on CDROM
- 16.Guliato D, Rangayyan RM, Carvalho JD, Santiago SA: Spiculation-preserving polygonal modeling of contours of breast tumors. Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pages 2791–2794, New York City, NY, September 2006 [DOI] [PubMed]
- 17.Guliato D, Rangayyan RM, Carvalho JD, Santiago SA: Polygonal modeling of contours with the preservation of spicules. IEEE Trans Biomed Eng, 2007, in press [DOI] [PubMed]
- 18.Rangayyan RM. Biomedical Image Analysis. Boca Raton, FL: CRC; 2005. [Google Scholar]
- 19.Pohlman S, Powell KA, Obuchowski NA, Chilcote WA, Grundfest-Broniatowski S. Quantitative classification of breast tumors in digitized mammograms. Med Phys. 1996;23(8):1337–1345. doi: 10.1118/1.597707. [DOI] [PubMed] [Google Scholar]
- 20.Niblack W, Yin J: A pseudo-distance measure for 2D shapes based on turning angle. IEEE International Conference on Image Processing, volume 3, pages 352–355, Washington DC, October 1995
- 21.Veltkamp RC, Tanase M: Part-based shape retrieval. Proceedings of the 13th Annual ACM International Conference on Multimedia, pages 543–546, Singapore, November 2005
- 22.Veltkamp RC, Tanase M, Sent D: Features in content-based image retrieval systems: a survey. In State-of-the-Art in Content-Based Image and Video Retrieval [Dagstuhl Seminar, 5–10 December 1999], pages 97–124, Deventer, The Netherlands: Kluwer, B.V., 2001
- 23.Veltkamp RC: Shape matching: Similarity measures and algorithm. IEEE SMI 2001 International Conference on Shape Modeling and Applications, pages 188–197, Genova, Italy, May 2001
- 24.Veltkamp RC. Shape algorithmics. Algorithmica. 2003;38(1):1–4. doi: 10.1007/s00453-003-1039-0. [DOI] [Google Scholar]
- 25.Latecki LJ, Lakämper R. Application of planar shape comparisons to object retrieval in image databases. Pattern Recogn. 2002;35(1):15–29. doi: 10.1016/S0031-3203(01)00039-5. [DOI] [Google Scholar]
- 26.Latecki LJ, Lakämper R, Wolter D: Shape similarity and visual parts. International Conference on Discrete Geometry for Computer Imagery (DGCI), pages 34–51, Napoles, Italy, 2003
- 27.Arkin EM, Chew LP, Huttenlocher DP, Kedem K, Mitchell JSB. An efficiently computable metric for comparing polygonal shapes. IEEE Trans Pattern Anal Mach Intell. 1991;13:209–216. doi: 10.1109/34.75509. [DOI] [Google Scholar]
- 28.Mandelbrot BB. The Fractal Geometry of Nature. San Francisco, CA: Freeman; 1983. [Google Scholar]
- 29.Peitgen HO, Jürgens H, Saupe D. Chaos and Fractals: New Frontiers of Science. New York, NY: Springer; 2004. [Google Scholar]
- 30.Deering W, West BJ. Fractal physiology. IEEE Eng Med Biol Mag. 1992;11(2):40–46. doi: 10.1109/51.139035. [DOI] [Google Scholar]
- 31.Schepers HE, Beek JHGM, Bassingthwaighte JB. Four methods to estimate the fractal dimension from self-affine signals. IEEE Eng Med Biol Mag. 1992;11(2):57–64. doi: 10.1109/51.139038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fortin C, Kumaresan R, Ohley W, Hoefer S. Fractal dimension in the analysis of medical images. IEEE Eng Med Biol Mag. 1992;11(2):65–71. doi: 10.1109/51.139039. [DOI] [Google Scholar]
- 33.Goldberger AL, Rigney DR, West BJ. Chaos and fractals in human physiology. Sci Am. 1990;262:42–49. doi: 10.1038/scientificamerican0290-42. [DOI] [PubMed] [Google Scholar]
- 34.Matsubara T, Fujita H, Kasai S, Goto M, Tani Y, Hara T, Endo T: Development of new schemes for detection and analysis of mammographic masses. In Proceedings of the 1997 IASTED International Conference on Intelligent Information Systems (IIS ’97), pages 63–66, Grand Bahama Island, Bahamas, December 1997
- 35.Screen Test: Alberta Program for the Early Detection of Breast Cancer—2001/03 Biennial Report. http://www.cancerboard.ab.ca/screentest, 2004
- 36.Alto H, Rangayyan RM, Paranjape RB, Desautels JEL, Bryant H. An indexed atlas of digital mammograms for computer-aided diagnosis of breast cancer. Annales des T’el’ecommunications. 2003;58(5–6):820–835. [Google Scholar]
- 37.The Mammographic Image Analysis Society digital mammogram database. http://peipa.essex.ac.uk/info/mias.html, accessed October 2006
- 38.Suckling J, Parker J, Dance DR, Astley S, Hutt I, Boggis CRM, Ricketts I, Stamatakis E, Cerneaz N, Kok SL, Taylor P, Betal D, Savage J: The Mammographic Image Analysis Society digital mammogram database. In Gale AG, Astley SM, Dance DR, and Cairns AY, editors, Proceedings of the 2nd International Workshop on Digital Mammography, volume 1069 of Excerpta Medica International Congress Series, pages 375–378, York, UK, July 1994
- 39.Metz CE. Basic principles of ROC analysis. Semin Nucl Med. 1978;VIII(4):283–298. doi: 10.1016/S0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]