Abstract
One of the main indicators for detecting changes in climate and marine ecosystems around the world is the sea surface temperature (SST). Even with several models presented in the literature, it is still a challenging task when only a single model is considered for SST forecasting. In this context, hybrid approaches that combine statistical models (to estimate linear dependencies) and machine learning models (to estimate nonlinear dependencies from residuals) have attained highlighted accuracy in several time series forecasting problems. In this way, this paper proposes a hybrid system that combines the autoregressive integrated moving average (ARIMA) model with a deep morphological neural network model, which employs dilation-erosion operators to estimate ARIMA’s model residuals. In this context, the proposed hybrid system is composed of three stages: (1) time series forecast using the ARIMA model, (2) residuals forecast using the deep morphological neural network and (3) a linear combination of the stages (1) and (2). Three SST time series are used in the experimental analysis. Moreover, the achieved results are evaluated using three relevant statistical measures showing that the proposed hybrid system attains higher accuracy when compared to other hybrid models in the literature.













Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
The datasets analyzed during the current study are available in the https://github.com/raaresearch/nca
Notes
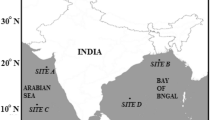
Available at https://www.pmel.noaa.gov/gtmba/pirata.
References
Mattos PSG, Cavalcanti GDC, Santos DSO, Silva EG (2022) Hybrid systems using residual modeling for sea surface temperature forecasting. Sci Rep 12:487
Abhiya AM, Minu S (2015) Ramachandrankizhur: salient long-term observations of SST along Kerala coast and its comparative variation with Lakshadweep coast. Aquatic Procedia 4:556–562
Kumar PKD, Paul YS, Muraleedharan KR, Murty VSN, Preenu PN (2016) Comparison of long-term variability of sea surface temperature in the Arabian sea and Bay of Bengal. Reg Stud Mar Sci 3:67–75
Bouali M, Sato OT, Polito PS (2017) Temporal trends in sea surface temperature gradients in the south Atlantic ocean. Remote Sens Environ 194:100–114
Chaidez V, Dreano D, Agusti S, Duarte CM, Hoteit I (2017) Decadal trends in red sea maximum surface temperature. Sci Rep 7(1):8144
Sohou Z, Kona V, Allada YCD, Djakoura S, Bouras B, Racape V, Degbe G, Adje C (2020) Seasonal and inter-annual onset sea surface temperature variability along the northern coast of the gulf of guinea. Reg Stud Mar Sci 35:101129
Shuva SH, Golder R, Rouf MA, Uddin MM, Bir J (2022) Daytime and nighttime sea surface temperature (SST) along with diurnal variability (D-SST) in the northern Bay of Bengal: a remote sensing approach. Int J Mar Sci 38:697–708
Xiao C, Chen N, Hu C, Wang K, Xu Z, Cai Y, Xu L, Chen Z, Gong J (2019) A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environ Modell Softw 120:104502
Smale DA, Wernberg T, Oliver ECJ, Thomsen M, Harvey BP, Straub SC, Burrows MT, Alexander LV, Benthuysen JA, Donat MG et al (2019) Marine heatwaves threaten global biodiversity and the provision of ecosystem services. Nat Clim Chang 9(4):306–312
Strong AE, Liu G, Meyer J, Hendee JC, Sasko D (2004) Coral reef watch 2002. Bull Mar Sci 75(2):259–268
Makwana M, Patnaik U (2021) Vulnerability of marine fisheries to sea surface temperature and cyclonic events: evidences across coastal India. Reg Stud Mar Sci 48:102002
Smith KE, Burrows MT, Hobday AJ, Gupta AS, Moore PJ, Thomsen M, Wernberg T, Smale DA (2021) Socioeconomic impacts of marine heatwaves: global issues and opportunities. Science 374(6566):3593
Holbrook NJ, Hernaman V, Koshiba S, Lako J, Kajtar JB, Amosa P, Singh A (2022) Impacts of marine heatwaves on tropical western and central pacific island nations and their communities. Global Planet Change 208:103680
Gentemann CL, Minnett PJ, Sienkiewicz J, DeMaria M, Cummings J, Jin Y, Doyle JD, Gramer L, Barron CN, Casey KS, Donlon CJ (2009) Misst: the multi-sensor improved sea surface temperature project. Oceanography 22:76
Singh P, Chowdary JS, Gnanaseelan C (2013) Impact of prolonged la Nina events on the Indian ocean with a special emphasis on southwest tropical Indian ocean SST. Global Planet Change 100:28–37
Minnett PJ (2019) Satellite remote sensing of sea surface temperatures. In: Cochran JK, Bokuniewicz HJ, Yager PL (eds) Encyclopedia of ocean sciences, 3rd edn. Academic Press, Oxford
Marinone SG, Gonzalez JI, Figueroa JM (2009) Prediction of currents and sea surface elevation in the gulf of California from tidal to seasonal scales. Environ Modell Softw 24(1):140–143
Bakker AMR, Applegate PJ, Keller K (2016) A simple, physically motivated model of sea-level contributions from the Greenland ice sheet in response to temperature changes. Environ Modell Softw 83:27–35
Schibalski A, Kleyer M, Maier M, Schrauder B (2022) Spatiotemporally explicit prediction of future ecosystem service provisioning in response to climate change, sea level rise, and adaptation strategies. Ecosyst Serv 54:101414
Cheriyan E, Rao AR, Sanilkumar KV (2022) Response of sea surface temperature, chlorophyll and particulate organic carbon to a tropical cyclonic storm over the arabian sea, southwest india. Dyn Atmos Oceans 97:101287
Serna FNM, Lo P, Enriquez EM, Cabanillas JMO, Villaseator HA, Covarrubias VH (2021) Copepod and monogenean infection of fish under sea surface temperature anomalies. J Sea Res 175:102098
Zhou Y, Yan W, Wei W (2021) Effect of sea surface temperature and precipitation on annual frequency of harmful algal blooms in the east china sea over the past decades. Environ Pollut 270:116224
Iskandar MR, Ismail MFA, Afrin T, Chandra H (2021) Marine heatwaves of sea surface temperature off south java. Heliyon 7(12):08618
Gao X, Li G, Liu J, Long SM (2022) The trend and interannual variability of marine heatwaves over the Bay of Bengal. Atmosphere 13(3):452
Kajtar JB, Hernaman V, Holbrook NJ, Petrelli P (2022) Tropical western and central pacific marine heatwave data calculated from gridded sea surface temperature observations and cmip6. Data Brief 40:107694
Li M, Huang W, Wu Q, Feng Y, Chen Y, Yu K, Chen B, Yang E, Meng L, Huang S, Wang X (2022) High genetic differentiation and moderate genetic diversity of the degenerative branching coral Pocillopora verrucosa in the tropical south china sea. Sci Total Environ 819:153076
Cho J, Yeh PJF, Lee YW, Kim H, Oki T, Kanae S, Kim W, Otsuki K (2010) A study on the relationship between Atlantic sea surface temperature and Amazonian greenness. Eco Inform 5(5):367–378
Salles R, Mattos P, Iorgulescu AMD, Bezerra E, Lima L, Ogasawara E (2016) Evaluating temporal aggregation for predicting the sea surface temperature of the Atlantic ocean. Eco Inform 36:94–105
Yu J, Zhang X, Li L, Shi C, Ye Y (2020) Salient difference of sea surface temperature over the North Atlantic in the spring following three super El Niño events. Environ Res Lett 15(9):094040
Box GEP, Jenkins GM, Reinsel GC (1994) Time series analysis: forecasting and control, 3rd edn. Prentice Hall, New Jersey
Mazaris AD, Kornaraki E, Matsinos YG, Margaritoulis D (2004) Modeling the effect of sea surface temperature on sea turtle nesting activities by investigating seasonal trends. Nat Resour Model 17(4):445–465
Rosmiati R, Liliasari S, Tjasyono B, Ramalis TR (2021) Development of ARIMA technique in determining the ocean climate prediction skills for pre-service teacher. J Phys Conf Ser 1731(1):012072
Oktaviani F, Miftahuddin-Setiawan I (2021) Forecasting sea surface temperature anomalies using the SARIMA ARCH/GARCH model. J Phys Conf Ser 1882(1):012020
Balogun AL, Adebisi N (2021) Sea level prediction using ARIMA, SVR and LSTM neural network: assessing the impact of ensemble ocean-atmospheric processes on models accuracy. Geomat Nat Haz Risk 12(1):653–674
Nawi WIAWM, Lola MS, Zakariya R, Zainuddin NH, Hamid AAKA, Aruchunan E, Nazzrol NSA (2021) Improved of forecasting sea surface temperature based on hybrid ARIMA and support vector machines models. Malays J Fundam Appl Sci 17:609–620
Tripathi KC, Das IML, Sahai AK (2006) Predictability of sea surface temperature anomalies in the Indian ocean using artificial neural networks. Indian J Mar Sci 35:210–220
Gorriz EG, Sanchez JG (2007) Prediction of sea surface temperatures in the western Mediterranean sea by neural networks using satellite observations. Geophys Res Lett 34(11):16425
Deo KPMC (2017) Prediction of daily sea surface temperature using efficient neural networks. Ocean Dyn 67(3–4):357–368
Wei L, Guan L, Qu L (2020) Prediction of sea surface temperature in the south china sea by artificial neural networks. IEEE Geosci Remote Sens Lett 17(4):558–562
Ryu D, Liang F, Mallick BK (2013) Sea surface temperature modeling using radial basis function networks with a dynamically weighted particle filter. J Am Stat Assoc 108(501):111–123
Mahongo S, Deo M (2013) Using artificial neural networks to forecast monthly and seasonal sea surface temperature anomalies in the western indian ocean. Int J Ocean Clim Syst 4:133–150
Zhang Q, Wang H, Dong J, Zhong G, Sun X (2017) Prediction of sea surface temperature using long short-term memory. IEEE Geosci Remote Sens Lett 14(10):1745–1749
Yang Y, Dong J, Sun X, Lima E, Mu Q, Wang X (2018) A CFCC–LSTM model for sea surface temperature prediction. IEEE Geosci Remote Sens Lett 15(2):207–211
Lin Y, Zhong G (2021) A multi-channel LSTM model for sea surface temperature prediction. J Phys Conf Ser 1880(1):012029
Li C, Feng Y, Sun T, Zhang X (2022) Long term Indian ocean dipole (IOD) index prediction used deep learning by convLSTM. Remote Sens 14(3):523
Usharani B (2022) ILF-LSTM: enhanced loss function in LSTM to predict the sea surface temperature. Soft Comput 2:1–13
Han M, Feng Y, Zhao X, Sun C, Hong F, Liu C (2019) A convolutional neural network using surface data to predict subsurface temperatures in the pacific ocean. IEEE Access 7:172816–172829
Walleshauser B, Bollt E (2022) Predicting sea surface temperatures with coupled reservoir computers. Nonlinear Process Geophys 29(3):255–264
Feng Y, Gao Z, Xiao H, Yang X, Song Z (2022) Predicting the tropical sea surface temperature diurnal cycle amplitude using an improved XGBoost algorithm. J Mar Sci Eng 10(11):1686
Sun T, Feng Y, Li C, Zhang X (2022) High precision sea surface temperature prediction of long period and large area in the Indian ocean based on the temporal convolutional network and internet of things. Sensors 22(4):1636
Zhang GP (2003) Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50:159–175
Pai P-F, Lin C-S (2005) A hybrid ARIMA and support vector machines model in stock price forecasting. Omega 33(6):497–505
Yan Q, Ma C (2016) Application of integrated ARIMA and RBF network for groundwater level forecasting. Environ Earth Sci 75(5):1–13
Domingos SdO, de Oliveira JF, de Mattos Neto PS (2019) An intelligent hybridization of ARIMA with machine learning models for time series forecasting. Knowl-Based Syst 175:72–86
Khashei M, Bijari M (2011) A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl Soft Comput 11(2):2664–2675
Ji L, Zou Y, He K, Zhu B (2019) Carbon futures price forecasting based with ARIMA–CNN–LSTM model. Procedia Comput Sci 162:33–38
Mirkalaei PM, Banihabib ME (2019) An ARIMA–NARX hybrid model for forecasting urban water consumption (case study: Tehran metropolis). Urban Water J 16:365–376
Dave E, Leonardo A, Jeanice M, Hanafiah N (2021) Forecasting Indonesia exports using a hybrid model ARIMA–LSTM. Procedia Comput Sci 179:480–487
de Oliveira JFL, Silva EG, de Mattos Neto PSG (2021) A hybrid system based on dynamic selection for time series forecasting. IEEE Trans Neural Netw Learn Syst 33:3251
Firmino PRA, de Mattos Neto PS, Ferreira TA (2015) Error modeling approach to improve time series forecasters. Neurocomputing 153:242–254
Chen K-Y, Wang C-H (2007) A hybrid SARIMA and support vector machines in forecasting the production values of the machinery industry in Taiwan. Expert Syst Appl 32(1):254–264
Faruk DÖ (2010) A hybrid neural network and ARIMA model for water quality time series prediction. Eng Appl Artif Intell 23(4):586–594
Cadenas E, Rivera W (2010) Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA–ANN model. Renew Energy 35(12):2732–2738
Wongsathan R, Seedadan I (2016) A hybrid ARIMA and neural networks model for pm-10 pollution estimation: the case of Chain Mai city moat area. Procedia Comput Sci 86:273–276
Zhou L, Xia J, Yu L, Wang Y, Shi Y, Cai S, Nie S (2016) Using a hybrid model to forecast the prevalence of schistosomiasis in humans. Int J Environ Res Public Health 13(4):355
Fraser A, Swinney H (1986) Independent coordinates for strange atractors from mutual information. Phys Rev A 33(2):1134–1140
Stojanovic MB, Bozic MM, Stankovic MM, Stajic ZP (2014) A methodology for training set instance selection using mutual information in time series prediction. Neurocomputing 141:236–245
de Araujo AR, Oliveira ALI, de Meira SR (2017) A morphological neural network for binary classification problems. Eng Appl Artif Intell 65:12–28
Pessoa LFC, Maragos P (2000) Neural networks with hybrid morphological rank linear nodes: a unifying framework with applications to handwritten character recognition. Pattern Recogn 33:945–960
Araújo RA, Nedjah N, Oliveira ALI, Meira SRL (2019) A deep increasing-decreasing-linear neural network for financial time series prediction. Neurocomputing 347:59–81
Friedman M (1940) A comparison of alternative tests of significance for the problem of \(m\) rankings. Ann Math Statist 11(1):86–92
Tukey JW (1949) Comparing individual means in the analysis of variance. Biometrics 5:99–114
Demsar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30
Funding
This work is partially supported by INES (www.ines.org.br), CNPq grant 465614/2014-0, FACEPE grants APQ-0399-1.03/17 and APQ/0388-1.03/14, CAPES grant 88887.136410/2017-00.
Author information
Authors and Affiliations
Contributions
RDA contributed to study conception and design, material preparation, data collection and analysis. PSDGMN contributed to study conception and design. NN contributed to material preparation and analysis. SCBS contributed to material preparation and analysis. The first draft of the manuscript was written by all authors, which commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: A partial derivatives equations
Appendix: A partial derivatives equations
From Eq. (10), \(\frac{\partial u^{(j)}_i}{\partial {\textbf{y}}^{(j-1)}}\) can be estimated by:
From Eqs. (13), \(\dot{f }(u^{(j)}_i)\) can be estimated by:
From Eq. (10), \(\frac{\partial u^{(j)}_i}{\partial \lambda ^{(j)}_i}\) can be estimated by:
At this point, we have a problem to evaluate derivatives \(\frac{\partial u^{(j)}_i}{\partial {\textbf{a}}^{(j)}_i}\) and \(\frac{\partial u^{(j)}_i}{\partial {\textbf{b}}^{(j)}_i}\) since dilation and erosion operations are not differentiable. In order to overcome such drawback, we employ the approach proposed by Pessoa and Maragos [69] and extended by Araújo et al. [68], using the concept of smoothed rank indicator vector to approximate morphological operators in terms of differentiable operations. Next, we show how to evaluate both derivatives.
The partial derivative \(\frac{\partial u^{(j)}_i}{\partial {\textbf{a}}^{(j)}_i}\) is given by:
in which
where \({\textbf {1}} = (1, \ldots , 1)\) and operation \(\cdot ^T\) denotes transposition.
Note that \(Q_\sigma ({\textbf{z}}) = [q_\sigma (z_1), q_\sigma (z_2), \ldots , q_\sigma (z_n)]\), in which the term \(q_\sigma (z_i)\) is given by:
where \(\sigma \) is a smoothing factor and n is the vector dimensionality.
The partial derivative \(\frac{\partial u^{(j)}_i}{\partial {\textbf{b}}^{(j)}_i}\) is estimated by:
in which
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Araújo, R.A., de Mattos Neto, P.S.G., Nedjah, N. et al. An error correction system for sea surface temperature prediction. Neural Comput & Applic 35, 11681–11699 (2023). https://doi.org/10.1007/s00521-023-08311-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-023-08311-8