An effective image compression–encryption scheme based on compressive sensing (CS) and game of life (GOL) | Neural Computing and Applications Skip to main content

Advertisement

Springer Nature Link
Log in

An effective image compression–encryption scheme based on compressive sensing (CS) and game of life (GOL)

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

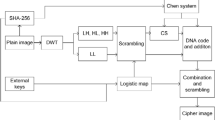
At present, information entropies of cipher images gotten by some CS-based image cryptosystems are lower than 7, which make them vulnerable to entropy attack. To cope with this problem, we propose a novel image compression–encryption method based on compressive sensing (CS) and game of life (GOL). Encryption architecture of permutation, compression and diffusion is utilized. Firstly, a plaintext-dependent game-of-life-based scrambling method is presented to shuffle the sparse coefficient matrix of plain image, and the permutation matrix is constructed by rules of GOL, which may effectively reduce the adjacent pixel correlation and enhance the scrambling effect. Secondly, the confused matrix is compressed by CS and diffused using a key matrix to get the cipher image. Additionally, a five-dimensional (5D) memristive hyperchaotic system is used to generate chaotic sequences. They are utilized to construct measurement matrix, to generate initial cell matrix of GOL and to produce key matrix. Information entropy of plain image and external key parameters are combined to compute initial values of the hyperchaotic system. Therefore, our algorithm has high sensitivity to original image and it may resist against known-plaintext attack and chosen-plaintext attack. Experimental results and performance analyses demonstrate that the proposed encryption algorithm is effective to withstand various typical attacks, and it may be applied for image secure communication.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Cao C, Sun KH, Liu WH (2018) A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process 143:122–133

    Google Scholar 

  2. Gan ZH, Chai XL, Han DJ, Chen YR (2019) A chaotic image encryption algorithm based on 3-D bit-plane permutation. Neural Comput Appl 31:7111–7130

    Google Scholar 

  3. Zahid AH, Arshad MJ, Ahmad M (2019) A novel construction of efficient substitution-boxes using cubic fractional transformation. Entropy 21:245

    MathSciNet  Google Scholar 

  4. Belazi A, Ei-Latif AAA, Diaconu AV, Rhouma R, Belghith S (2017) Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt Lasers Eng 88:37–50

    Google Scholar 

  5. Liu S, Guo CL, Sheridan JT (2014) A review of optical image encryption techniques. Opt Laser Technol 57:327–342

    Google Scholar 

  6. Li XW, Lee I-K (2015) Modified computational integral imaging-based double image encryption using fractional Fourier transform. Opt Lasers Eng 66:112–121

    Google Scholar 

  7. Wang XY, Xu DH (2014) A novel image encryption scheme based on Brownian motion and PWLCM chaotic system. Nonlinear Dyn 75:345–353

    Google Scholar 

  8. Chen JX, Zhu ZL, Zhang LB, Zhang YS, Yang BQ (2018) Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption. Signal Process 142:340–353

    Google Scholar 

  9. Zhang LM, Sun KH, Liu WH, He SB (2017) A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations. Chin Phys B 26:100504

    Google Scholar 

  10. Wu Y, Zhou YC, Noonan JP, Agaian S (2014) Design of image cipher using latin squares. Inf Sci 264:317–339

    MathSciNet  MATH  Google Scholar 

  11. Chen JX, Zhu ZL, Fu C, Zhang LB, Zhang YS (2015) An efficient image encryption scheme using lookup table-based confusion and diffusion. Nonlinear Dyn 81:1151–1166

    Google Scholar 

  12. Wu XJ, Kan HB, Kurths J (2015) A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl Soft Comput 37:24–39

    Google Scholar 

  13. Hua ZY, Xu BX, Jin F, Huang HJ (2019) Image encryption using josephus problem and filtering diffusion. IEEE Access 7:8660–8674

    Google Scholar 

  14. Donoho DL (2006) Compressed sensing. IEEE Trans Inf Theory 52:1289–1306

    MathSciNet  MATH  Google Scholar 

  15. Candes EJ, Romberg J, Tao T (2006) Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 52:489–509

    MathSciNet  MATH  Google Scholar 

  16. Baraniuk RG (2007) Compressive sensing. IEEE Signal Process Mag 24:118–121

    Google Scholar 

  17. Huang H, He X, Xiang Y, Wen WX, Zhang YS (2018) A compression–diffusion–permutation strategy for securing image. Signal Process 150:183–190

    Google Scholar 

  18. Chai XL, Wu HY, Gan ZH, Zhang YS, Chen YR, Nixon KW (2020) An efficient visually meaningful image compression and encryption scheme based on compressive sensing and dynamic LSB embedding. Opt Lasers Eng 124:105837

    Google Scholar 

  19. Ponuma R, Amutha R (2018) Compressive sensing based image compression–encryption using novel 1D-chaotic map. Multimed Tools Appl 77:19209–19234

    Google Scholar 

  20. Deng J, Zhao S, Wang Y, Wang L, Wang H, Sha H (2017) Image compression–encryption scheme combining 2D compressive sensing with discrete fractional random transform. Multimed Tools Appl 76:10097–10117

    Google Scholar 

  21. Chen JX, Zhang YS, Zhang LY (2017) On the security of optical ciphers under the architecture of compressed sensing combining with double random phase encoding. IEEE Photonics J 9:7802611

    Google Scholar 

  22. Zhou NR, Pan SM, Li HL, Wang D, Zhou YC (2015) Image compression and encryption scheme based on 2D compressive sensing and fractional Mellin transform. Opt Commun 343:10–21

    Google Scholar 

  23. Zhang YS, Zhou JT, Chen F, Zhang Leo Y, Xiao D, Chen B, Liao XF (2016) A block compressive sensing based scalable encryption framework for protecting significant image regions. Int J Bifurc Chaos 26:1650191

    MATH  Google Scholar 

  24. Chen JX, Zhang Y, Qi L, Fu C, Xu LS (2018) Exploiting chaos-based compressed sensing and cryptographic algorithm for image encryption and compression. Opt Laser Technol 99:238–248

    Google Scholar 

  25. Zhou NR, Zhang AD, Zheng F, Gong LHC (2014) Novel image compression–encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing. Opt Laser Technol 62:152–160

    Google Scholar 

  26. Zhou NR, Jiang H, Gong LH, Xie XW (2018) Double-image compression and encryption algorithm based on co-sparse representation and random pixel exchanging. Opt Lasers Eng 110:72–79

    Google Scholar 

  27. Gong LH, Qiu KD, Deng CZ, Zhou NR (2019) An image compression and encryption algorithm based on chaotic system and compressive sensing. Opt Laser Technol 115:257–267

    Google Scholar 

  28. Zhou NR, Pan SM, Cheng S, Zhou YC (2016) Image compression–encryption scheme based on hyper-chaotic system and 2D compressive sensing. Opt Laser Technol 82:121–133

    Google Scholar 

  29. Rawat N, Kim B, Kumar R (2016) Fast digital image encryption based on compressive sensing using structurally random matrices and Arnold transform technique. Optik 127:2282–2286

    Google Scholar 

  30. Liu H, Xiao D, Zhang R, Zhang YS, Bai S (2016) Robust and hierarchical watermarking of encrypted images based on compressive sensing. Signal Process Image 45:41–51

    Google Scholar 

  31. Fang H, Vorobyov SA, Jiang H, Taheri O (2014) Permutation meets parallel compressed sensing: how to relax restricted isometry property for 2D sparse signals. IEEE Trans Signal Process 62:196–210

    MathSciNet  MATH  Google Scholar 

  32. Zhang YS, Zhou JT, Chen F, Zhang Leo Y, Wong K-W, He X, Xiao D (2016) Embedding cryptographic features in compressive sensing. Neurocomputing 205:472–480

    Google Scholar 

  33. Tong XJ, Zhang M, Wang Z, Ma J (2016) A joint color image encryption and compression scheme based on hyper-chaotic system. Nonlinear Dyn 84:2333–2356

    Google Scholar 

  34. Chai XL, Zheng XY, Gan ZH, Hua DJ, Chen YR (2018) An image encryption algorithm based on chaotic system and compressive sensing. Signal Process 148:124–144

    Google Scholar 

  35. Chai XL, Gan ZH, Chen YR, Zhang YS (2017) A visually secure image encryption scheme based on compressive sensing. Signal Process 134:35–51

    Google Scholar 

  36. Wang H, Xiao D, Li M, Xiang YP, Li XY (2019) A visually secure image encryption scheme based on parallel compressive sensing. Signal Process 155:218–232

    Google Scholar 

  37. Xiao D, Cai HK, Zheng HY (2015) A joint image encryption and watermarking algorithm based on compressive sensing and chaotic map. Chin Phys B 24(6):060505

    Google Scholar 

  38. Chen TH, Zhang M, Wu JH, Yuen C, Tong Y (2016) Image encryption and compression based on kronecker compressed sensing and elementary cellular automata scrambling. Opt Laser Technol 84:118–133

    Google Scholar 

  39. Hu GQ, Xiao D, Wang Y, Xiang T (2017) An image coding scheme using parallel compressive sensing for simultaneous compression–encryption applications. J Vis Commun Image Represent 44:116–127

    Google Scholar 

  40. Cambareri V, Mangia M, Pareschi F, Rovatti R, Setti G (2015) Low-complexity multiclass encryption by compressed sensing. IEEE Trans Signal Process 63:2183–2195

    MathSciNet  MATH  Google Scholar 

  41. Liu DD, Zhang W, Yu H, Zhu ZL (2018) An image encryption scheme using self-adaptive selective permutation and inter-intra feedback diffusion. Signal Process 151:130–143

    Google Scholar 

  42. Souyah A, Faraoun KM (2016) An image encryption scheme combining chaos-memory cellular automata and weighted histogram. Nonlinear Dyn 86(1):639–653

    MathSciNet  Google Scholar 

  43. Enayatifar R, Sadaei HJ, Abdullah AH, Lee M, Isnin IF (2015) A novel chaotic based image encryption using a hybrid model of deoxyribonucleic acid and cellular automata. Opt Laser Eng 71:33–41

    Google Scholar 

  44. Dalhoum ALA, Mahafzah BA, Awwad AA, Aldhamari I, Ortega A, Alfonseca M (2012) Digital image scrambling using 2D cellular automata. IEEE Multimed 19(4):28–36

    Google Scholar 

  45. Niyat AY, Moattar MH, Torshiz MN (2017) Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt Lasers Eng 90:225–237

    Google Scholar 

  46. Murugan B, Gounder AGN, Manohar S (2016) A hybrid image encryption algorithm using chaos and Conway’s game-of-life cellular automata. Secur Commun Netw 9(7):634–651

    Google Scholar 

  47. Kechaidou MG, Sirakoulis GC (2017) Game of life variations for image scrambling. J Comput Sci 21:432–447

    Google Scholar 

  48. Chai XL, Fu XL, Gan ZH, Zhang YS, Lu Y, Chen YR (2018) An efficient chaos-based image compression and encryption scheme using block compressive sensing and elementary cellular automata. Neural Comput Appl. https://doi.org/10.1007/s00521-018-3913-3

    Article  Google Scholar 

  49. Xiang T, Liao XF, Wong K (2007) An improved particle swarm optimization algorithm combined with piecewise linear chaotic map. Appl Math Comput 190:1637–1645

    MathSciNet  MATH  Google Scholar 

  50. Wikipedia. http://en.wikipedia.org/wiki/Conway’s_Game_of_Life2011

  51. Min FH, Wang ZL, Cao Y, Wang ER (2018) Multistability analysis of a dual-memristor circuit based on hyperbolic function. Acta Electron Sin 46:486–494

    Google Scholar 

  52. Guo JB, Wang R (2014) Construction of a circulant compressive measurement matrix based on chaotic sequence and RIPless theory. Acta Phys Sin 63(19):373–382

    Google Scholar 

  53. Zhou NR, Yang JP, Tan CF, Pan SM, Zhou ZH (2015) Double-image encryption scheme combining DWT-based compressive sensing with discrete fractional random transform. Opt Commun 354:112–121

    Google Scholar 

  54. Liu H, Wen F, Kadir A (2018) Construction of a new 2D Chebyshev–Sine map and its application to color image encryption. Multimed Tools Appl. https://doi.org/10.1007/s11042-018-6996-z

    Article  Google Scholar 

  55. Wang XY, Guo K (2014) A new image alternate encryption algorithm based on chaotic map. Nonlinear Dyn 76:1943–1950

    MATH  Google Scholar 

  56. Liu HJ, Kadir A, Gong PJ (2015) A fast color image encryption scheme using one-time S-boxes based on complex chaotic system and random noise. Opt Commun 338:340–347

    Google Scholar 

  57. Zhang YQ, Wang XY (2014) A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice. Inf Sci 273:329–351

    Google Scholar 

  58. Chai XL, Chen YR, Broyde L (2017) A novel chaos-based image encryption algorithm using DNA sequence operations. Opt Lasers Eng 88:197–213

    Google Scholar 

  59. Chai XL, Yang K, Gan ZH (2017) A new chaos-based image encryption algorithm with dynamic key selection mechanisms. Multimed Tools Appl 76:9907–9927

    Google Scholar 

  60. Chai XL (2017) An image encryption algorithm based on bit level Brownian motion and new chaotic systems. Multimed Tools Appl 76:1159–1175

    Google Scholar 

  61. Ye GD (2014) A block image encryption algorithm based on wave transmission and chaotic systems. Nonlinear Dyn 75:417–427

    Google Scholar 

  62. Luo YL, Zhou RL, Liu JX, Cao Y, Ding XM (2018) A parallel image encryption algorithm based on the piecewise linear chaotic map and hyper-chaotic map. Nonlinear Dyn 93:1165–1181

    Google Scholar 

  63. Xu L, Li Z, Li J, Hua W (2016) A novel bit-level image encryption algorithm based on chaotic maps. Opt Lasers Eng 78:17–25

    Google Scholar 

  64. Yang FF, Mou J, Liu J, Ma CG, Yan HZ (2020) Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process 169:107373

    Google Scholar 

  65. Li CQ, Lin DD, Feng BB, Lu JH (2018) Cryptanalysis of a chaotic image encryption algorithm based on information entropy. IEEE Access 6:75834–75842

    Google Scholar 

  66. Li CQ, Lin DD, Lu JH, Hao F (2018) Cryptanalyzing an image encryption algorithm based on autoblocking electrocardiography. IEEE Multimed 25:46–56

    Google Scholar 

  67. Zhang YL, Liu YS, Wang C, Zhou JT, Zhang YS, Chen GR (2018) Improved known-plaintext attack to permutation-only multimedia ciphers. Inf Sci 430–431:228–239

    MathSciNet  Google Scholar 

  68. Chen JX, Han FF, Qian W, Yao YD, Zhu ZL (2018) Cryptanalysis and improvement in an image encryption scheme using combination of the 1D chaotic map. Nonlinear Dyn 93:2399–2413

    Google Scholar 

  69. Li CQ, Lin DD, Lu JH (2017) Cryptanalyzing an image-scrambling encryption algorithm of pixel bits. IEEE Multimed 24:64–71

    Google Scholar 

  70. Li C, Zhang Y, Xie EY (2019) When an attacker meets a cipher-image in 2018: a year in review. J Inf Secur Appl 48:102361

    Google Scholar 

  71. Zhou YC, Cao WJ, Chen CLP (2014) Image encryption using binary bit plane. Signal Process 100(7):197–207

    Google Scholar 

Download references

Acknowledgements

All the authors are deeply grateful to the editors for smooth and fast handling of the manuscript. The authors would also like to thank the anonymous referees for their valuable suggestions to improve the quality of this paper. This work is supported by the National Natural Science Foundation of China (Grant Nos. U1604145, 61802111, 61872125, 61871175), Science and Technology Foundation of Henan Province of China (Grant No. 182102210027, 182102410051), China Postdoctoral Science Foundation (Grant Nos. 2018T110723, 2016M602235), Key Scientific Research Projects for Colleges and Universities of Henan Province (Grant No. 19A413001), CERNET NGI Technology Innovation Project (Grant No. NGII20170902), Chongqing Key Laboratory of Mobile Communications Technology (Grant No. cqupt-mct-201901), Graduate Education Innovation and Quality Improvement Project of Henan University (Grant No. SYL18020105) and Henan Higher Education Teaching Reform Research and Practice Project (Graduate Education) (Grant No. 2019SJGLX080Y).

Author information

Authors and Affiliations

  1. School of Software, Intelligent Data Processing Engineering Research Center of Henan Province, Institute of Intelligent Network System, Henan University, Kaifeng, 475004, China

    Zhihua Gan

  2. School of Computer and Information Engineering, Henan Key Laboratory of Big Data Analysis and Processing, Henan University, Kaifeng, 475004, China

    Xiuli Chai & Jitong Zhang

  3. College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, China

    Yushu Zhang

  4. School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing, 400065, China

    Yushu Zhang

  5. Department of Electrical and Computer Engineering, Duke University, Durham, NC, 27708, USA

    Yiran Chen

Authors
  1. Zhihua Gan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiuli Chai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jitong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yushu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yiran Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiuli Chai.

Ethics declarations

Conflict of interest

All authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gan, Z., Chai, X., Zhang, J. et al. An effective image compression–encryption scheme based on compressive sensing (CS) and game of life (GOL). Neural Comput & Applic 32, 14113–14141 (2020). https://doi.org/10.1007/s00521-020-04808-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-020-04808-8

Keywords

Search

Navigation