Evolutionary game analysis for non-cooperative behavior of entities in a closed-loop green supply chain under government intervention

Abstract

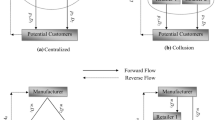
Decentralized behavior of entities in a green supply chain plays a significant role in pricing and green innovation effort to produce more environment-friendly products at affordable prices. Government intervention (e.g., subsidy for green production, Cap-and-Trade Policy (CTP)) is a crucial component for diminishing carbon emissions due to manufacturing of new products and recycling of used products. In this study, we investigate the long-term decentralized behavior of supply chain members and the evolutionary stable decision of the government to intervene in price and sales effort competition among retailers. More precisely, through an evolutionary game theoretic framework, we look for the non-cooperative behavior of the population of retailers investing in sales efforts towards the manufacturer who invests in green level of the products, under government intervention and CTP. The model is further extended to analyze the evolutionary behavior of the population of government whether it intervenes or not in the same situation. Our study demonstrates that the whole population of retailers adopts the retailer-led Stackelberg strategy to deal with the manufacturer, and the most significant finding is that, in such a situation, government intervention is always favorable regardless of what the supply chain decides. Numerical results exhibit that whenever retailers dominate the market, it becomes beneficial for both retailers as well as the entire supply chain, and the environmental performance of the product also increases compared to the vertical Nash scenario.

Appendices

Appendix A

Proof of Proposition 1

In (N,N) strategy combination, to obtain the optimal decisions, we solve simultaneously for the retailers’ and the manufacturer’s profit functions.

The first order of partial derivatives of the retailers’ profit function is

$$\begin{aligned} \frac{\partial \Pi _r^{ij}}{\partial \textrm{P}_ij}= & {} a - 2\alpha \textrm{P}_{ij} + \beta \textrm{P}_{ji} +\gamma A_{ij} - \delta A_{ji} + \lambda \theta _{ij} +\alpha w \nonumber \\ \frac{\partial \Pi _r^{ij}}{\partial A_ij}= & {} \gamma (\textrm{P}_{ij} - w) - \xi A_{ij} \end{aligned}$$

(29)

The second-order partial derivatives are

$$\begin{aligned} \frac{\partial ^2 \Pi _r^{ij}}{\partial \textrm{P}_{ij}^2}= & {} -2\alpha< 0\\ \frac{\partial ^2 \Pi _r^{ij}}{\partial A_{ij}^2}= & {} -\xi < 0\\ \frac{\partial ^2 \Pi _r^{ij}}{\partial \textrm{P}_{ij} \partial A_{ij}}= & {} \gamma \end{aligned}$$

Hence the negative definiteness of the Hessian matrix holds for $2\alpha \xi - \gamma ^2 > 0$. The retailer’s payoff function can be shown to be concave in $\textrm{P}_{ij}$ and $A_{ij}$. From the first-order optimality conditions, we get

$$\begin{aligned} \textrm{P}_{NN}(\theta _ij)= & {} \frac{\xi (\alpha w +a +\lambda \theta _{ij}) - w\gamma (\gamma - \delta )}{\xi (2 \alpha - \beta ) - \gamma (\gamma - \delta )} \end{aligned}$$

(30)

$$\begin{aligned} A_{NN}(\theta _{ij})= & {} \frac{\gamma \big [(a +\lambda \theta _{ij}) - w(\alpha - \beta )}{\xi (2 \alpha - \beta ) - \gamma (\gamma - \delta )} \end{aligned}$$

(31)

The first partial derivative of the manufacturer’s profit function is $\frac{\partial \Pi _m^{ij}}{\partial \theta _{ij}} = a - (2\alpha - \beta )\textrm{P}_{NN}(\theta _{ij}) + (\gamma - \delta )A_{NN}(\theta _{ij}) + \lambda \theta _{ij} + \alpha w$

Now, the second partial derivative of the manufacturer’s profit function is

$$\begin{aligned} \frac{\partial ^2 \Pi _m^{ij}(\theta _{ij})}{\partial \theta _{ij}^2} = 4\lambda \psi _1 - \eta \end{aligned}$$

Clearly the manufacturer’s profit function is concave in $\theta _{ij}$ for $4\lambda \psi _1 - \eta < 0$.

Now, from the first-order optimality condition for the manufacturer’s profit, we obtain

$$\begin{aligned}{} & {} \theta _{NN}(\textrm{P}_{NN}, A_{NN}) \\{} & {} \quad = \frac{\left( \begin{array}{c}\psi _1 \{2a - 2(\alpha - \beta ) \textrm{P}_{NN} + 2(\gamma - \delta )A_{NN}\} + 2\lambda (w - \psi _2) \end{array} \right) }{\eta - 4\lambda \psi _1} \end{aligned}$$

Substituting (30) and (31) in $\theta _{NN}(\textrm{P}_{NN},A_{NN})$, we obtain

$$\begin{aligned} \theta _{NN} = \frac{\left( \begin{array}{c} 2(a\alpha \xi \psi _1 - \lambda \psi _2\psi _3) - 2w\{\alpha \xi \psi _1(\alpha - \beta ) - \lambda \psi _3\} \end{array} \right) }{\eta \psi _3 - 2\lambda \psi _1(\psi _3 + \xi \alpha )} \end{aligned}$$

where $\psi _3 = \xi (2\alpha - \beta ) - \gamma (\gamma - \delta )$. To ease computational complexity, we substitute $X_1 = 2(a\alpha \xi \psi _1 - \lambda \psi _2\psi _3)$, $X_2 = 2\{\alpha \xi \psi _1(\alpha - \beta ) - \lambda \psi _3\}$ and $\Xi _1 = \eta \psi _3 - 2\lambda \psi _1(\psi _3 + \xi \alpha )$ and get

$$\begin{aligned} \theta _{NN}= & {} \frac{X_1 - wX_2}{\Xi _1} \end{aligned}$$

(32)

Again, substituting (32) in (30) and (31), we obtain $p_{NN}$ and $A_{NN}$. $\square$

Proof of Proposition 4

In (S, S) strategy combination, to obtain the optimal decisions, we apply backward induction for the retailers and the manufacturer’s profit functions.

The first derivative of the manufacturer’s profit function is

$$\begin{aligned} \frac{\partial \Pi _m^{ij}}{\partial \theta _{ij}}{} & {} = \psi _1\{2a - (\alpha - \beta )(\textrm{P}_{ij} + \textrm{P}_{ji}) + (\gamma - \delta )(A_{ij} \nonumber \\{} & {} \quad + A_{ji})\}+ 2\lambda (w - \psi _2) + (4\lambda \psi _1 - \eta )\theta _{ij} \end{aligned}$$

(33)

The second-order derivative is

$$\begin{aligned} \frac{\partial ^2 \Pi _m^{ij}}{\partial \theta _{ij}^2}= & {} 4\lambda \psi _1 - \eta \end{aligned}$$

(34)

The retailer’s payoff function is concave in $\theta _{ij}$ for $4\lambda \psi _1 - \eta < 0$. Hence, using the first-order optimality condition, we get

$$\begin{aligned} \theta _{ij} = \frac{\psi _1 \{2a - (\alpha -\beta )(\textrm{P}_{ij} + \textrm{P}_{ji}) + (\gamma - \delta )(A_{ij}+A_{ji})\} + 2\lambda (w - \psi _2)}{\eta - 4\lambda \psi _1}\nonumber \\ \end{aligned}$$

(35)

Now, substituting (35) in the retailer’s payoff function and a similar manner, using the optimality conditions, we obtain $p_{SS}$ and $A_{SS}$. Using these in (35), finally, we obtain $\theta _{SS}$.

In this case, the second-order partial derivatives are

$$\begin{aligned} \frac{\partial ^2 \Pi _r^{ij}}{\partial \textrm{P}_{ij}^2}= & {} -\frac{2\{ (\eta - 3\lambda \psi _1)\alpha - \beta \lambda \psi _1\}}{\eta - 4\lambda \psi _1}\\ \frac{\partial ^2 \Pi _r^{ij}}{\partial \textrm{P}_{ij} \partial A_{ij}}= & {} \frac{\gamma (\eta - 3\lambda \psi _1) - \delta \lambda \psi _1}{\eta - 4\lambda \psi _1}, ~~\frac{\partial ^2 \Pi _r^{ij}}{\partial A_{ij}^2} = -\xi < 0 \end{aligned}$$

Here, the Hessian matrix is negative definite provided the conditions

max{$\frac{\gamma ^2}{2\alpha }, \frac{(3\gamma +\lambda )^2}{8(3\alpha + \beta )}$} < $\xi$ < $\frac{\gamma (3\gamma + \delta )}{2(7\alpha - \beta )}$ and $4\lambda \psi _1 - \eta < 0$ hold.

Similarly, we can easily prove Propositions 2 and 3. $\square$

Appendix B

The proof of Proposition 6 is the same as those of Propositions 1 and 4.

Proof of Proposition 7

To evaluate the equilibrium point of the system of differential equations, we use the first-order conditions $\frac{dx}{dt}=0$ and $\frac{dy}{dt}=0$.

Clearly (0,0), (1,0),(0,1) and (1,1) are the equilibrium points.

Using the stability condition to find another equilibrium point when $0< x,~ y < 1$, we get

$$\begin{aligned}{} & {} x(1-x) \big [ y(\Pi _{SC}^{N,I} - \Pi _{SC}^{S,I}) + (1-y)(\Pi _{SC}^{N,NI} - \Pi _{SC}^{S,NI})\big ] = 0\nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}{} & {} y(1-y) \big [ x(\Pi _{G}^{N,I} - \Pi _{G}^{N,NI}) + (1-x)(\Pi _{G}^{S,I} - \Pi _{G}^{S,NI})\big ] = 0\nonumber \\ \end{aligned}$$

(37)

From Eqs. (36) and (37), we get

$$\begin{aligned}{} & {} x^* = \frac{\Pi _{SC}^{N,NI} - \Pi _{SC}^{S,NI}}{(\Pi _{SC}^{N,I} - \Pi _{SC}^{N,NI}) + \Pi _{SC}^{S,NI}-\Pi _{SC}^{S,I})} \end{aligned}$$

(38)

$$\begin{aligned}{} & {} y^* = \frac{\Pi _G^{S,I} - \Pi _G^{S,NI}}{(\Pi _G^{N,I} - \Pi _G^{N,NI}) + \Pi _G^{S,NI}-\Pi _G^{S,I})}. \end{aligned}$$

(39)

Thus we get all the equilibrium points in Proposition 6. $\square$

Proof of Corollary 2

From the Jacobian matrix, we get

$$\begin{aligned} \textrm{tr}(J){} & {} = (1-2x)\{y(\Pi _r^{N,I}-\Pi _r^{S,I}) + (1-y)(\Pi _r^{N,NI} \nonumber \\{} & {} \quad - \Pi _r{S,NI})\}+ (1-2y)\{x(\Pi _G^{N,I}-\pi _G^{N,NI}) \nonumber \\{} & {} \quad + (1-x)(\Pi _g^{S,I} - \Pi _G^{S,NI})\} \end{aligned}$$

(40)

$$\begin{aligned} \textrm{det}(J){} & {} = (1-2x)(1-2y)\{y(\Pi _r^{N,I}-\Pi _r^{S,I}) \nonumber \\{} & {} \quad + (1-y)(\Pi _r^{N,NI} - \Pi _r{S,NI})\}+ \{x(\Pi _G^{N,I}-\pi _G^{N,NI}) \nonumber \\{} & {} \quad + (1-x)(\Pi _g^{S,I} - \Pi _G^{S,NI})\} \end{aligned}$$

(41)

Since from Proposition 6, $\Pi _r^{N,NI}=\Pi _r^{S,NI}$ and $\Pi _G^{N,NI}=\Pi _G^{S,NI}$ so we find that both (0,0) and (1,0) are not equilibrium points. $\square$