Novel pricing strategies for revenue maximization and demand learning using an exploration–exploitation framework

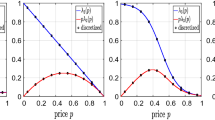
Abstract

The price demand relation is a fundamental concept that models how price affects the sale of a product. It is critical to have an accurate estimate of its parameters, as it will impact the company’s revenue. The learning has to be performed very efficiently using a small window of a few test points, because of the rapid changes in price demand parameters due to seasonality and fluctuations. However, there are conflicting goals when seeking the two objectives of revenue maximization and demand learning, known as the learn/earn trade-off. This is akin to the exploration/exploitation trade-off that we encounter in machine learning and optimization algorithms. In this paper, we consider the problem of price demand function estimation, taking into account its exploration–exploitation characteristic. We design a new objective function that combines both aspects. This objective function is essentially the revenue minus a term that measures the error in parameter estimates. Recursive algorithms that optimize this objective function are derived. The proposed method outperforms other existing approaches.

Derivation of utility derivatives for the three proposed formulations

1.1 Formulation 1

According to Section 5, the expected utility of our first formulation is defined as:

$$\begin{aligned}&E[U(p^*)_n]= b{p^*}^2+ap^*-\eta \frac{1}{2 \sqrt{tr[\Sigma _{\beta (n)}]}}\nonumber \\&\quad tr\Big [{1\over {\gamma }}\Sigma _{\beta }(n-1)-{{\Sigma _{\beta }(n-1)x_n {x_n}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x_n}^T\Sigma _{\beta }(n-1)}x_n}\Big ] \end{aligned}$$

The first derivative of the expected utility, $\frac{\partial E[U(p^*)_n]}{\partial p^*}$, can be calculated as:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}=a+2bp^* -\eta \frac{1}{2 \sqrt{tr[\Sigma _{\beta (n)}]}}\nonumber \\&\quad \frac{\partial tr[{1\over {\gamma }}\Sigma _{\beta }(n-1)-{{\Sigma _{\beta }(n-1)x_n {x_n}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x_n}^T\Sigma _{\beta }(n-1)}x_n}]}{\partial p^*} \end{aligned}$$

(38)

Since $tr[A+B]=tr[A]+tr[B]$, then $\frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*}$ would be:

$$\begin{aligned}&\frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*}=\frac{\partial tr[{1\over {\gamma }}\Sigma _{\beta }(n-1)]}{\partial p^*}\nonumber \\&\quad -\frac{\partial tr[{{\Sigma _{\beta }(n-1)x_n {x_n}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x_n}^T\Sigma _{\beta }(n-1)}x_n}]}{\partial p^*} \end{aligned}$$

(39)

It can be observed that the first derivative term in Eq. (39) evaluates to zero. Evaluating the second term of Eq. (39), and letting $x_n$ be denoted as $x^*$:

$$\begin{aligned}&\frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*} = \frac{\partial tr[{{\Sigma _{\beta }(n-1){x^*}{x^*}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x^*}^T\Sigma _{\beta }(n-1)}{x^*}}]}{\partial p^*} \end{aligned}$$

(40)

Let $A= \frac{{x^*}{x^*}^T\Sigma _{\beta }(n-1)}{\sigma ^2\gamma ^2+\gamma {x^*}^T \Sigma _{\beta }(n-1){x^*}}$, accordingly Eq. (40) can be evaluated as follows:

$$\begin{aligned}&\quad \frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*}= \frac{\partial tr[{{\Sigma _{\beta }(n-1)A\Sigma _{\beta }(n-1)}}]}{\partial p^*} \end{aligned}$$

(41)

However, from trace properties $tr[BAC]=tr[ACB]$, then:

$$\begin{aligned}&\frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*} = \frac{\partial tr[{{A{\Sigma _{\beta }^2(n-1)}}}]}{\partial p^*} \end{aligned}$$

(42)

Then, from trace derivative properties:

$$\begin{aligned} \frac{\partial tr[AB]}{\partial x}= & {} \frac{\partial<A^T,B>_F}{\partial x} \nonumber \\= & {} <B^T,\frac{\partial A}{\partial x}>_F +<A^T,\frac{\partial B}{\partial x}>_F \nonumber \\= & {} tr[B\frac{\partial A}{\partial x}+A\frac{\partial B}{\partial x}] \end{aligned}$$

(43)

Accordingly, substitute from Eq.(43) into Eq. (42) where $B={\Sigma _{\beta }^2(n-1)}$ and $x=p^*$, accordingly $\frac{\partial B}{\partial x}$ evaluates to zero, and Eq. (42) is simplified to:

$$\begin{aligned}&\frac{\partial tr[{\Sigma _\beta }(n)]}{\partial p^*}= tr\left[ {\Sigma _{\beta }^2(n-1)}\frac{\partial A}{\partial p^*}\right] \end{aligned}$$

(44)

Simplifying matrix A:

$$\begin{aligned} A=\frac{\begin{pmatrix} 1&{} p^* \\ p^* &{} {p^*}^2 \end{pmatrix}}{\sigma ^2\gamma ^2+\gamma [{\sigma _a^2}+2\sigma _{ab}p^*+{\sigma _b}^2{p^*}^2]} \end{aligned}$$

(45)

where $\Sigma _\beta (n-1)= \begin{pmatrix} {\sigma _a}^2&{} \sigma _{ab} \\ \sigma _{ab} &{} {\sigma _b}^2 \end{pmatrix}$.

Then, evaluating $\frac{\partial A}{\partial p^*}$:

$$\begin{aligned}&\frac{\partial A}{\partial p^*} =\frac{1}{{(\sigma ^2\gamma ^2+\gamma ({\sigma _a^2}+2\sigma _{ab}p^*+{\sigma _b}^2{p^*}^2))}^2}\nonumber \\&\quad \Big [{(\sigma ^2\gamma ^2+\gamma ({\sigma _a^2}+2\sigma _{ab}p^*+{\sigma _b}^2{p^*}^2))}\begin{pmatrix} 0&{} 1 \\ 1 &{} 2{p^*} \end{pmatrix}\nonumber \\&\quad -\gamma \begin{pmatrix}1&{} p^* \\ p^* &{} {p^*}^2 \end{pmatrix}(2\sigma _{ab}+2\sigma _b^2 p^*)\Big ] \end{aligned}$$

(46)

Let $g(p^*)={(\sigma ^2\gamma ^2+\gamma [{\sigma _a^2}+2\sigma _{ab}p^*+{\sigma _b}^2{p^*}^2])}$, then:

$$\begin{aligned}&\frac{\partial A}{\partial p^*}=\frac{1}{{g^2(p^*)}}Z(p*)=\frac{1}{{g^2(p^*)}}{\begin{pmatrix}Z_{11} &{} Z_{12} \\ Z_{12}&{} Z_{22}\end{pmatrix}} \end{aligned}$$

(47)

where $Z(p*)$ matrix elements: $Z_{11}$, $Z_{12}$, and $Z_{22}$ are evaluated as follows:

$$\begin{aligned} Z_{11}= & {} -2\gamma (\sigma _{ab}+{\sigma _b}^2 p^*) \nonumber \\ Z_{12}= & {} \gamma (\sigma ^2\gamma +\sigma _a^2-\sigma _b^2{p^*}^2) \nonumber \\ Z_{22}= & {} \gamma (2\sigma ^2\gamma p^* +2\sigma _a^2p^*+2\sigma _{ab}{p^*}^2) \end{aligned}$$

(48)

Substituting from Eq. (44) and Eq. (47) into Eq. (38):

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}=a+2bp^* \nonumber \\&\quad + \eta \frac{1}{2 \sqrt{tr[\Sigma _{\beta (n)}]}}tr\big [{\frac{1}{{g^2(p^*)}}\Sigma _{\beta }^2(n-1)Z(p*)}\big ] \end{aligned}$$

(49)

1.2 Formulation 2

As presented in Section 5, as defined in Section 5, can be evaluated as follows:

$$\begin{aligned}&E[U(p^*)_n]=E[R(p^*)_n] -\eta \Big (\frac{\sqrt{\Sigma _\beta (n)_{11}}}{a}+\frac{\sqrt{\Sigma _\beta (n)_{22}}}{|b|}\Big ) \end{aligned}$$

Using Eq. (7) to substitute for $\Sigma _\beta (n)$, and let $A=\Sigma _\beta (n-1)x^*{x^*}^T\Sigma _\beta (n-1)$, and calculate the derivative of utility $\frac{\partial E[U(p^*)_n]}{\partial p^*}$ with respect to $p^*$, this results in the following equation:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+2bp^*\nonumber \\&\quad +\eta \Bigg (\frac{1}{2a\sqrt{{\Sigma _\beta }(n)_{11}}} \frac{\partial }{\partial p^*}\bigg [\frac{A_{11}}{g(p^*)}\bigg ]\nonumber \\&\quad +\frac{1}{2|b|\sqrt{{\Sigma _\beta }(n)_{22}}} \frac{\partial }{\partial p^*}\bigg [\frac{A_{22}}{g(p^*)}\bigg ]\Bigg ) \end{aligned}$$

(50)

where $A_{11}$ is the first row and column entry in matrix A. $A_{11}$ and $A_{22}$ are evaluated as follows:

$$\begin{aligned} A_{11}= & {} {\sigma _{ab}}^2{p^*}^2+2{\sigma _a}^2\sigma _{ab}p^*+{\sigma _a}^4\nonumber \\ A_{22}= & {} {\sigma _{b}}^4{p^*}^2+2{\sigma _{ab}}{\sigma _b}^2 p^*+{\sigma _{ab}}^2 \end{aligned}$$

(51)

Substituting Eq. (51) into Eq. (50) and evaluating $\frac{\partial }{\partial p^*}[\frac{A_{11}}{g(p^*)}]$ and $\frac{\partial }{\partial p^*}[\frac{A_{22}}{g(p^*)}]$ terms results in:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*} = a+2bp^*\nonumber \\&\quad + \eta \bigg ( \Big [\frac{2g(p^*)(\sigma _{ab}{\sigma _a}^2+\sigma _{ab}^2p^*)-2\gamma A_{11}(\sigma _{ab}+\sigma _b^2p^*)}{2a g^2(p^*)\sqrt{{\Sigma _\beta }_{11}(n)}}\Big ]\nonumber \\&\quad +\Big [\frac{2g(p^*)(\sigma _{ab}{\sigma _b}^2+\sigma _{b}^4p^*)-2\gamma A_{22}(\sigma _{ab}+\sigma _b^2p^*))}{2bg^2(p^*)\sqrt{{\Sigma _\beta }_{22}(n)}}\Big ]\bigg )\nonumber \\ \end{aligned}$$

(52)

Simplifying Eq. (52) results in the following equation:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*} = a+2bp^* + \eta \frac{\gamma }{2ag^2(p^*)\sqrt{{\Sigma _\beta }_{11}(n)}} \times \nonumber \\&\Big ({p^*}^2({\sigma _{ab}}^3-\sigma _{ab}\sigma _a^2\sigma _b^2)\nonumber \\&\quad +p^*(\sigma ^2\gamma \sigma _{ab}^2-\sigma _a^4\sigma _b^2)+\sigma ^2\gamma \sigma _a^2\sigma _{ab}\Big ) \nonumber \\&\quad + \eta \frac{\gamma }{2|b|\sqrt{{\Sigma _\beta }_{22}(n)}g^2(p^*)} \Big (p^*(\sigma ^2\gamma \sigma _{b}^4\nonumber \\&\quad -\sigma _{ab}^2\sigma _b^2+ \sigma _b^4\sigma _a^2)+(\sigma ^2\gamma \sigma _{ab}\sigma _b^2\nonumber \\&\quad +\sigma _b^2\sigma _a^2\sigma _{ab}-\sigma _{ab}^3)\Big ) \end{aligned}$$

(53)

1.3 Formulation 3

The expected utility of the third proposed formulation, the expected utility of our second formulation is defined as:

$$\begin{aligned} E[U(p^*)_n]=E[R(p^*)_n]-\eta {p^*} \sqrt{{x^*}^T\Sigma _{\beta (n-1)} x^*+\sigma ^2} \end{aligned}$$

The derivative of the expected utility $U(p^*)_n$ w.r.t. $p^*$ is calculated as follows:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+2bp^*\nonumber \\&\quad - \frac{\eta }{2\sqrt{{p^*}^2({x^*}^T\Sigma _{\beta (n-1)} x^*+\sigma ^2)}}\nonumber \\&\quad \frac{\partial \Big ({p^*}^2({x^*}^T\Sigma _{\beta (n-1)} x^* +\sigma ^2)\Big )}{\partial p^*} \end{aligned}$$

(54)

where $\Sigma _\beta (n-1)=\begin{pmatrix}{\sigma _a}^2&{} \sigma _{ab} \\ \sigma _{ab} &{} {\sigma _b}^2 \end{pmatrix}$. Thus, the derivative of expected utility with respect to $p^*$, $\frac{\partial E[U(p^*)_n]}{\partial p^*}$ can be simplified into:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+ 2bp^*\nonumber \\&\quad - \frac{\eta \Big (2p^*({\sigma _a}^2+2\sigma _{ab}p^*+{p^*}^2{\sigma _b}^2+\sigma ^2)+2{p^*}^2(\sigma _{ab}+{\sigma _b}^2p^*)\Big )}{2\sqrt{{p^*}^2({x^*}^T\Sigma _{\beta (n-1)} x^*+\sigma ^2)}}\nonumber \\ \end{aligned}$$

(55)

Simplifying Eq. (55) results in the following equation:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+2bp^*\nonumber \\&\quad -\eta \frac{{2{\sigma _b}^2{p^*}^2 +3\sigma _{ab}p^*+\sigma _a}^2+\sigma ^2}{\sqrt{(\sigma ^2+\sigma _a^2+2\sigma _{ab}p^*+\sigma _b^2{p^*}^2)}} \end{aligned}$$

(56)