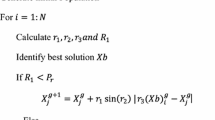Abstract
Recent developments designate the quick growing of optimization meta-heuristics in the domain of optimization. Sine–cosine optimizer is a stochastic technique that generates various preliminary random research agents global optimal solutions and involves them to fluctuate toward or outwards the superior global optima solution utilizing a mathematical model based on sine and cosine trigonometry functions. Nevertheless, standard SCA provides insufficient global optima results on complex dimension functions illustrating poor convergence rate. The search process of the SCA method holds various shortcomings such as slow convergence, weak balance amid exploration and exploitation, and inefficiency in convergence. To overcome these shortcomings in this work, we are trying to present a new heuristic approach based on merging the features of SCA (sine–cosine approach) with a HS (harmony search approach) known as HSCAHS algorithm. The existing approach integrates the merits of the sine–cosine algorithm and HS algorithm to reduce demerits, like the trapping in local optima and unbalanced exploitation. The new approach presents own work performance in two different stages; firstly, the sine–cosine algorithm starts the explore procedure to augment exploration capability. Secondly, harmony search part starts its search from SCA finds so far to augment the exploitation tendencies. Hence, hybrid approach can find best possible solution in which least time improves the exploitation and exploration. Hence, the newly existing hybrid approach can be quickly convergent, statistically sound and more robust. The capability of the hybrid approach is verified by applying it on eighteen tested benchmark, economic dispatch, three-bar truss design, rolling element bearing design, multiple disc clutch brake design, speed reducer design and planetary gear train design problems. The experimental solutions reveal that the hybrid approach is able to finding the superior quality of optimal goal (or solution) of the optimize functions in most cases in comparison with others.










Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Simpson AR, Dandy GC, Murphy LJ (1994) Genetic algorithms compared to other techniques for pipe optimization. J Water Resour Plan Manag 120(4):423–443
BoussaïD I, Lepagnot J, Siarry P (2013) A survey on optimization metaheuristics. Inf Sci 237:82–117
Parejo JA, Ruiz-Cortés A, Lozano S, Fernandez P (2012) Metaheuristic optimization frameworks: a survey and benchmarking. Soft Comput 16(3):527–561
Zakeri E, Moezi SA, Bazargan-Lari Y, Zare A (2017) Multi-tracker optimization algorithm: a general algorithm for solving engineering optimization problems. Iran J Sci Technol Trans Mech Eng 41(4):315–341
Xue B, Zhang M, Browne WN, Yao X (2016) A survey on evolutionary computation approaches to feature selection. IEEE Trans Evol Comput 20(4):606–626
Bozorg-Haddad O (2018) Advanced optimization by nature-inspired algorithms. Springer, Berlin
Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S (2019) Henry gas solubility optimization: a novel physics-based algorithm. Futur Gener Comput Syst 101:646–667
Dommel H, Tinney W (1968) Optimal power flow solutions. IEEE Trans Power Appar Syst 87(10):1866–1876
Chung TS, Li YZ (2001) A hybrid GA approach for OPF with consideration of facts devices. IEEE Power Eng Rev 1(1):47–50
Cai LJ, Erlich I, Stamtsis G (2004) Optimal choice and allocation of facts devices in deregulated electricity market using genetic algorithms. IEEE 1(1):1–10
Kennedy J, Eberhart RC (1995) Particle swarm optimization. Proc IEEE Int Conf Neural Netw 1:1942–1948
Soares J, Sousa T, Vale ZA, Morais H, Faria P (2011) Ant colony search algorithm for the optimal power flow problem. IEEE Power Energy Soc Gen Meet 1(1):1–8
Kumar Kalaiselvi V, Chandrasekar K (2010-II) Enhanced genetic algorithm for optimal electric power flow using TCSC and TCP. In: Proceedings of World, vol 1, pp 1–8
Kumar KV, Chandrasekar K (2002) Optimal power flow by enhanced genetic algorithm. IEEE Trans Power Syst 17(2):229–236
Slimani L, Bouktir T (2012) Optimal power flow solution of the Algerian electrical network using DA. Telkomnika 10(1):199–210
Hsun LR, Ren TS, Tone CY, Tseng WT (2011) Optimal power flow by a fuzzy based hybrid particle swarm optimization approach. Electr Power Syst Res 81(7):1466–1476
Sinsupan N, Leeton U, Kulwora WT (2010) Application of harmony search to optimal power flow problems. IEEE Xplore 1(1):219–222
Ben-Tal A, El haoui L, Nemirovski A, (2009) Robust optimization. Princeton Ser Appl Math 1(1):9–16
Chowdhury BH (1992) Towards the concept of integrated security: optimal dispatch under static and dynamic security constraints. Electr Power Syst Res 25(1):213–225
Simon D (2008) Biogeography-based optimization. IEEE Trans Evolut Comput 12(6):702–713
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimization. Adv Eng Softw 69(1):46–61
Abido MA (2002) Optimal power flow using Tabu search algorithm. Electr Power Comput Syst 30(1):469–483
Mukherjee A, Mukherjee V (2015) Solution of optimal power flow using chaotic krill herd algorithm. Chaos Solitons Fractals 78(1):10–21
Mirjalili S (2015) The ant lion optimizer. Adv Eng Sofw 83(1):80–98
Duman S, Güvenç U, Sönmez Y, Yörökeren N (2012) Optimal power flow using gravitational search algorithm. Energy Converg Manag 59(1):86–95
Mirjalili S (2016) SCA: a sine cosine algorithm for solving optimization problems. Knowledge-based systems. Elsevier, Amsterdam, pp 120–133
Mirjalili S (2016) Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl 4(1):1053–1073
Bouchekara HREH (2014) Optimal power flow using black-hole-based optimization approach. Appl Soft Comput 24(1):879–888
Mirjalili S (2016) The whale optimization algorithm. Adv Eng Softw 9(1):51–67
Daryani N, Hagh MT, Teimourzadeh S (2016) Adaptive group search optimization algorithm for multi-objective optimal power flow problem. Appl Soft Comput 38(1):1012–1024
Daryani N, Hagh MT, Teimourzadeh S (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 2(1):495–513
Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst 89(1):228–249
Mirjalili S (2013) Optimal power flow using cuckoo optimization algorithm. Ijareeie 1(1):4213–4218
Mirjalili S (2016) Grasshopper optimization algorithm: theory and application. Adv Eng Softw 105(1):30–47
Singh N, Singh SB (2011) One half global best position particle swarm optimization algorithm. Int J Sci Eng Res 2(8):1–10
Singh N, Singh SB (2012) Personal best position particle swarm optimization. J Appl Comput Sci Math 12(6):69–76
Singh N, Singh S, Singh SB (2012) Half mean particle swarm optimization algorithm. Int J Sci Eng Res 3(8):1–9
Singh N, Hachimi H (2018) A new hybrid whale optimizer algorithm with mean strategy of grey wolf optimizer for global optimization. Math Comput Appl 23(14):1–32
Singh N, Singh S, Singh SB (2012) HPSO: a new version of particle swarm optimization algorithm. J Artif Intell 3(3):123–134
Singh N (2017) Singh SB (2012) Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance. J Appl Math 2030489:1–15
Singh N, Singh SB (2017) A new hybrid MGBPOSA-GSA variant for improving function optimization solution in search space. Evolut Biol 13(1):1–13
Singh N, Singh SB (2017) A novel hybrid GWO-SCA approach for optimization problems. Eng Sci Technol Int J 20(6):1586–1601
Singh N, Singh SB (2017) A modified mean grey wolf optimization approach for benchmark and biomedical problems. Evolut Biol 13(1):1–28
Singh N (2019) A modified variant of grey wolf optimizer. Sci Iran Int J Sci Technol 1(1):1–31
Singh N, Singh SB, Houssein EH (2020) Hybridizing salp swarm algorithm with particle swarm optimization algorithm for recent optimization functions. Evol Intell 1(1):1–31. https://doi.org/10.1007/s12065-020-00486-6
Kaur M, Kaur R, Singh N, Dhiman G (2020) Schoa: An newly fusion of sine and cosine with chimp optimization algorithm for HLS of datapaths in digital filters and engineering applications. Comput Eng 1(1):1–36. https://doi.org/10.1007/s00366-020-01233-2
Singh N, Son LH, Chiclana F, Magnot JP (2020) A new fusion of SALP swarm with sine cosine for optimization of non-linear functions. Comput Eng 36(1):185–212. https://doi.org/10.1007/s00366-018-00696-8
Alresheedi SS, Lu S, Elaziz MA, Ewees AA (2019) Improved multiobjective SALP swarm optimization for virtual machine placement in cloud computing. HCIS 9(1):15
Zhao H, Huang G, Yan N (2018) Forecasting energy-related co2 emissions employing a novel SSA-LSSVM model: considering structural factors in China. Energies 11(4):781
Asaithambi S, Rajappa M (2018) Swarm intelligence-based approach for optimal design of CMOS differential amplifier and comparator circuit using a hybrid SALP swarm algorithm. Rev Sci Instrum 89(5):
Faris H, Mafarja MM, Heidari AA, Aljarah I, Ala’M A-Z, Mirjalili S, Fujita H (2018) An efficient binary SALP swarm algorithm with crossover scheme for feature selection problems. Knowl-Based Syst 154:43–67
Yang B, Zhong L, Zhang X, Shu H, Yu T, Li H, Jiang L, Sun L (2019) Novel bio-inspired memetic SALP swarm algorithm and application to MPPT for PV systems considering partial shading condition. J Clean Prod 215:1203–1222
Barik AK, Das DC, Active power management of isolated renewable microgrid generating power from rooftop solar arrays, sewage waters and solid urban wastes of a smart city using SALP swarm algorithm, in, (2018) Technologies for Smart-City Energy Security and Power (ICSESP). IEEE 2018:1–6
El-Fergany AA (2018) Extracting optimal parameters of PEM fuel cells using SALP swarm optimizer. Renew Energy 119:641–648
Baygi SMH, Karsaz A, Elahi A, A hybrid optimal PID-fuzzy control design for seismic exited structural system against earthquake: a SALP swarm algorithm. In: 6th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS). IEEE, pp 220–225
Kurtulus E, Yildiz AR, Sait SM, Bureerat S (2020) A novel hybrid Harris Hawks-simulated annealing algorithm and RBF-based metamodel for design optimization of highway guardrails. Mater Test 62(3):251–260. https://doi.org/10.3139/120.111478
Yildiz BS (2020) Optimal design of automobile structures using moth-flame optimization algorithm and response surface methodology. Materials Test 62(4):371–377. https://doi.org/10.3139/120.11149
Yildiz BS (2020) The mine blast algorithm for the structural optimization of electrical vehicle components. Mater Test 62(5):497–501. https://doi.org/10.3139/120.111511
Ozkaya H, Yildiz M, Yildiz AR, Bureerat S, Yildiz BS, Sait SM (2020) The equilibrium optimization algorithm and the response surface-based meta model for optimal structural design of vehicle components. Mater Test 62(5):492–496. https://doi.org/10.3139/120.111509
Yildiz AR, Yildiz BS, Sait SM, Li X (2019) The Harris Hawks, grasshopper and multi-verse optimization algorithms for the selection of optimal machining parameters in manufacturing operations. Mater Test 61(8):725–733. https://doi.org/10.3139/120.111377
Yildiz AR, Yildiz BS, Sait SM, Pholdee SB (2019) A new hybrid Harris Hawks Nelder-mead optimization algorithm for solving design and manufacturing problems. Mater Test 61(8):735–743. https://doi.org/10.3139/120.111378
Yildiz BS, Yildiz AR (2019) The Harris hawks optimization algorithm, SALP swarm algorithm, grasshopper optimization algorithm and dragonfly algorithm for structural design optimization of vehicle components. Mater Test 61(8):744–748. https://doi.org/10.3139/120.111379
Yildiz BS (2020) The spotted hyena optimization algorithm for weight-reduction of automobile brake components. Mater Test 62(4):383–388. https://doi.org/10.3139/120.111495
Yildiz BS, Yildiz AR, Albak EI, Abderazek H, Sait SM, Bureerat S (2020) Butterfly optimization algorithm for optimum shape design of automobile suspension components. Mater Test 62(4):365–370. https://doi.org/10.3139/120.111492
Yildiz BS, Yildiz AR (2018) Comparison of grey wolf, whale, water cycle, ant lion and sine-cosine algorithms for the optimization of a vehicle engine connecting rod. Mater Test 60(3):311–315. https://doi.org/10.3139/120.111153
Yildiz BS, Yildiz AR (2017) Moth-flame optimization algorithm to determine optimal machining parameters in manufacturing processes. Mater Test 59(5):425–429. https://doi.org/10.3139/120.111024
Yildiz AR (2019) A novel hybrid whale nelder mead algorithm for optimization of design and manufacturing problems. Int J Adv Manuf Technol. https://doi.org/10.1007/s00170-019-04532-1
Abderazek H, Yildiz AR, Mirjalili S (2019) Comparison of recent optimization algorithms for design optimization of a cam-follower mechanism. Knowl Based Syst. https://doi.org/10.1016/j.knosys.2019.105237
Hamza F, Abderazek H, Lakhdar S et al (2018) Optimum design of cam-roller follower mechanism using a new evolutionary algorithm. Int J Adv Manuf Technol 99:1267–1282. https://doi.org/10.1007/s00170-018-2543-3
Yildiz BS (2017) Natural frequency optimization of vehicle components using the interior search algorithm. Mater Test 59(5):456–458. https://doi.org/10.3139/120.111018
Geem ZW, H KJ, V LG, (2001) A new heuristic optimization algorithm: harmony search. Simulation 17(12):4831–4845
Geem ZW (2009) Music-inspired harmony search algorithm: theory and application, music-inspired harmony search algorithm: theory and applications, Berlin, Germany
Yuan X, Dai X, Zhao J, He Q (2014) On a novel multi-swarm fruit fly optimization algorithm and its application. Appl Math Comput 233(3):260–271
Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18
Singh N, Singh S, Singh SB (2017) A new hybrid MGBPO-GSA variant for improving function optimization solution in search space. Evol Biol 13(1):1–13
Mirjalili S (2015) Moth-flame optimization algorithm. A novel nature-inspired heuristic paradigm. Knowl Based Syst 89(1):228–249
Gandomi AH, S YX, Alavi AH, (2013) Cuckoo search algorithm: a meta-heuristic approach to solve structural optimization problems. Eng Comput 29(1):17–35
Lu Y, Zhou Y, Wu X (2017) A hybrid lightning search algorithm-simplex method for global optimization. Discrete Dyn Nat Soc 8342694:1–23
Zhang M, Luo W, Wang X (2008) Differential evolution with dynamic stochastic selection for constrained optimization. Inform Sci 178(15):3043–3074
Liu CZ, Wang HY (2010) Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. J Appl Soft Comput 10(2):629–640
Sadollah A, Bahreininejad A, Eskandar H, Hamdi M (2013) Enhanced genetic algorithm for optimal electric power flow using TCSC and TCPS. J Appl Soft Comput 13(5):2592–2612
Chakraborty I, Kumar V, Nair SB, Tiwari R (2003) Rolling element bearing design through genetic algorithms. Eng Optim 35(6):649–659
Dhiman G (2019) Esa: a hybrid bio-inspired metaheuristic optimization approach for engineering problems. Eng Comput 37:323–353
Zhu H, Hu Y, Zhu W (2019) A dynamic adaptive particle swarm optimization and genetic algorithm for different constrained engineering design optimization problems. Adv Nonlinear Dyn Vib Mech Syst 11(3):1–27
Pa S, D B, GV D, (2006) Teeth-number synthesis of a multi-speed planetary transmission using an estimation of distribution algorithm. ASME J Mech Des 10:108–115
Savsani P, Savsani V (2016) Passing vehicle search (PVA): a novel metaheuristic algorithm. Appl Math Model 40:3951–3978
Acknowledgements
We would like to thank the anonymous referees for their valuable comments that permitted to improve the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Dr. Narinder Singh and Mrs. Jaspreet Kaur declare that they have no conflict of interest.
Research involving human participants and/or animals
Harmony search approach was firstly developed by Z.W. Geem et al. Geem et al. (2001), Geem (2009). The combination search is a music-inspired optimization technique. It is inspired by the criticism that the aim of music is to search for a perfect state of harmony.
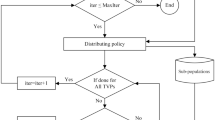
On the other side, Seyedali Mirjalili Mirjalili (2016a) developed a new nature-inspired approach known as sine–cosine algorithm (SCA) for solving different types of application of separate fields. This approach establishes the solution of various basic random agents and enables them to exclude them from a mathematical model based on the trigonometric sine and cosine functions as the best possible outcomes. I have studied theoretical models developed by various researchers, viz. genetic algorithm (GA) Chung and Li (2001), Cai et al. (2004), particle swarm optimization (PSO) Kennedy and Eberhart (1995), ant colony optimization (ACO) Soares et al. (2011), differential evolution (DE) Kumar and Chandrasekar (2010), Kumar and Chandrasekar (2002), hybrid genetic algorithm (HGA) Slimani and Bouktir (2012), fuzzy-based hybrid particle swarm optimization (fuzzy HPSO) Hsun et al. (2011), harmony search algorithm Sinsupan et al. (2010), robust optimization (RO) Ben-Tal et al. (2009), artificial neural network (ANN) Chowdhury (1992), biogeography-based optimization algorithm (BBO) Simon (2008), gray wolf optimization (GWO) Mirjalili et al. (2014), tabu search (TS) Abido (2002), krill herd algorithm (KHA) Mukherjee and Mukherjee (2015), ant lion optimizer (ALO) Mirjalili (2015a), gravitational search algorithm (GSA) Duman et al. (2012), sine–cosine algorithm (SCA) Mirjalili (2016a), dragonfly algorithm (DA) Mirjalili (2016b), black hole-based optimization (BHBO) Bouchekara (2014), whale optimization algorithm (WOA) Mirjalili (2016c), adaptive group search optimization (AGSO) Daryani et al. (2016a), multi-verse optimizer (MVO) Daryani et al. (2016b), moth flame optimizer (MFO) Mirjalili (2015b), cuckoo search (CS) Mirjalili (2013), grasshopper optimization algorithm (GOA) Mirjalili (2016d), one half personal best position particle swarm optimization (OHGBPPSO) Singh and Singh (2011), personal best position particle swarm optimization (PBPPSO) Singh and Singh (2012a), half mean particle swarm optimization algorithm (HMPSO) Singh et al. (2012a), HAGWO Singh and Hachimi (2018), hybrid particle swarm optimization (HPSO) Singh et al. (2012b), HPSOGWO Singh and Singh (2012b), hybrid MGBPSO-GSA Singh and Singh (2017a), HGWOSCA Singh and Singh (2017b), MGWO Singh and Singh (2017c), MVGWO Singh (2019), HSSAPSO Singh et al. (2020), SChoA Kaur et al. (2020), HSSASCA Singh et al. (2020) and many more. Based on the work done by these authors, we have also proposed an hybrid approach, namely “hybrid sine–cosine algorithm–harmony search algorithm (HSCAHS)”. With this method, it is proposed to increase the convergence quality of the sine–cosine algorithm by accelerating the explore seeking instead of letting the approach running numerous iterations without any perfection. The new hybrid approach has been tested with numerous well-known standard test functions and some real-life applications. All experimental solutions ensured that the newer current access is a strong search approach for different compatibility applications. This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
No human/animal was involved in the current study. So informed consent is not applicable on my study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Benchmark test suites

Appendix
A: Welded beam design problem
Consider \(\vec {x}=\left[ {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right] =\left[ h\,l\,t\,b \right] \)
-
\(\text {Minimize } f\left( {\vec {x}} \right) =1.10471x_{1}^{2}{{x}_{2}}+0.04811{{x}_{3}}{{x}_{4}}\left( 14.0+{{x}_{2}} \right) \)
-
Subject to:
-
\({{g}_{1}}\left( {\vec {x}} \right) =\tau \left( {\vec {x}} \right) -13600\le 0\)
-
\({{g}_{2}}\left( {\vec {x}} \right) =\sigma \left( {\vec {x}} \right) -30000\le 0 \)
-
\({{g}_{3}}\left( {\vec {x}} \right) ={{x}_{1}}-{{x}_{4}}\le 0\)
-
\({{g}_{4}}\left( {\vec {x}} \right) =0.10471\left( x_{1}^{2} \right) +0.04811{{x}_{3}}{{x}_{4}}\left( 14+{{x}_{2}} \right) -5.0\le 0\)
-
\({{g}_{6}}\left( {\vec {x}} \right) =\delta \left( {\vec {x}} \right) -0.25\le 0\)
-
\({{g}_{7}}\left( {\vec {x}} \right) =6000-{{p}_{c}}\left( {\vec {x}} \right) \le 0\)
-
where
-
\(\tau \left( {\vec {x}} \right) =\sqrt{\left( {{\tau }'} \right) +\left( 2{\tau }'{\tau }'' \right) \frac{{{x}_{2}}}{2R}+{{\left( {{\tau }''} \right) }^{2}}}\)
-
\({\tau }'=\frac{6000}{\sqrt{2}{{x}_{1}}{{x}_{2}}}\)
-
\({\tau }''=\frac{MR}{J}\)
-
\(M=6000\left( 14+\frac{{{x}_{2}}}{2} \right) \)
-
\(R=\sqrt{\frac{x_{2}^{2}}{4}+{{\left( \frac{{{x}_{1}}+{{x}_{3}}}{2} \right) }^{2}}}\)
-
\(j=2\left\{ {{x}_{1}}{{x}_{2}}\sqrt{2}\left[ \frac{x_{2}^{2}}{12}+{{\left( \frac{{{x}_{1}}+{{x}_{3}}}{2} \right) }^{2}} \right] \right\} \)
-
\(\sigma \left( {\vec {x}} \right) =\frac{504000}{{{x}_{4}}x_{3}^{2}}\)
-
\(\delta \left( {\vec {x}} \right) =\frac{65856000}{\left( 30\times {{10}^{6}} \right) {{x}_{4}}x_{3}^{3}}\)
-
\({{p}_{c}}\left( {\vec {x}} \right) =\frac{4.013\left( 30\times {{10}^{6}} \right) \sqrt{\frac{x_{3}^{2}x_{4}^{6}}{36}}}{196}\left( 1-\frac{{{x}_{3}}\sqrt{\frac{30\times {{10}^{6}}}{4\left( 12\times {{10}^{6}} \right) }}}{28} \right) \)
-
\(\text {with } 0.1\le {{x}_{1}},{{x}_{4}}\le 2.0\,and\,0.1\le {{x}_{2}},{{x}_{3}}\le 10.0 \)
B: Tension/compression spring design problem
Consider:
-
\( \vec {x}=\left[ {{x}_{1}}{{x}_{2}}{{x}_{3}} \right] =\left[ d\,D\,N \right] \)
-
\(\text {Minimize } f\left( {\vec {x}} \right) =\left( {{x}_{3}}+2 \right) {{x}_{2}}x_{1}^{2} \)
-
\(\text {subject to: }\)
-
\({{g}_{1}}\left( {\vec {x}} \right) =1-\frac{x_{2}^{3}{{x}_{3}}}{71785x_{1}^{4}}\le 0\)
-
\({{g}_{2}}\left( {\vec {x}} \right) =\frac{4x_{2}^{2}-{{x}_{1}}{{x}_{2}}}{12566\left( {{x}_{2}}x_{1}^{3}-x_{1}^{4} \right) }+\frac{1}{5108x_{1}^{2}}-1\le 0\)
-
\({{g}_{3}}\left( {\vec {x}} \right) =1-\frac{140.45{{x}_{1}}}{x_{2}^{2}{{x}_{3}}}\le 0\)
-
\({{g}_{4}}\left( {\vec {x}} \right) =\frac{{{x}_{1}}+{{x}_{2}}}{1.5}-1\le 0\)
-
\(\text {with } 0.05\le {{x}_{1}}\le 2.0,0.25\le {{x}_{2}}\le 1.3,and\,2.0\le {{x}_{3}}\le 15.0\)
C: Rolling element bearing design problem
\(\text {Maximum}[C_d(X)] ={\left\{ \begin{array}{ll}max(-f_cz^{2/3}D_b^{1.8}) &{} if D_b =\le 25.5mm 0\\ max(-3.647f_cz^{2/3}D_b^{1.4}) &{} if D_b =\le 25.5mm \end{array}\right. }\)
-
\(\text {Subject to: }\)
-
\(g_1(x)=\frac{\phi _0}{2\sin ^{-1}(D_b/D_m)}-Z+1\ge 0, \)
-
\(g_2(x)=2D_b-K_{D_{min}}(D-d)\ge 0,\)
-
\(g_3(x)=K_{D_{max}}(D-d)-2D_b\ge 0,\)
-
\(g_4(x)=\zeta B_w-D_b\ge 0,\)
-
\(g_5(x)=D_m-0.5(D+d)\ge 0,\)
-
\(g_6(x)=(0.5+e)(D+d)-D_m\ge 0,\)
-
\(g_7(x)=0.5(D-D_m-D_b)-\zeta D_b\ge 0,\)
-
\(g_8(x)=f_1\ge 0.515,\)
-
\(g_9(x)=f_0\ge 0.515,\)
-
where
-
\(f_c=37.91[1+[1.04(\frac{1-\gamma }{1+\gamma })^{1.72}] (\frac{f_i(2f_0-1)}{f_i-1})^{0.41}]^{10/3}]^{-0.3}\)
-
\(\gamma = \frac{D_b\cos \alpha }{D_m},\)
-
\(f_1=\frac{r_1}{D_b}\)
-
\(\phi _0=2\pi -20 \cos ^{-1}[\frac{(D-d)/2-3(T/4)^2+[D/2-(T/4-D_b)^2]-[d/2+(T/4)]^2]}{[2(D-d/2-3(T/4)][(T/4)-D_b]}]\)
-
\(T=D-d-2D_b,\)
-
\(D=160, d=90, B_w=30,\)
-
\(0.5(D+d)\le D_m\le 0.6(D+d),\)
-
\(0.15(D-d)\le D_b\le 0.45(D-d),\)
-
\(4\le Z\le 50, 0.515 \le f_1\le 0.6, 0.515\le f_0 \le 0.6,\)
-
\(0.4 \le K_{D_{min}}\le 0.5, 0.6 \le K_{D_{max}}\le 0.7,\)
-
\(0.3\le \epsilon \le 0.4, 0.02\le e \le 0.1, 0.6\le \xi \le 0.85\)
D: Multiple disc clutch brake design problem
-
\(Minimize f(x) = \pi (r_0^2-r_i^2)(Z+1)\rho t\)
-
s.t ;
-
\(g_1(x)=r_0-r_i-\Delta r\geqslant 0\)
-
\(g_2(x)=l_max-(Z+1)(t+\delta )\geqslant 0\)
-
\(g_3(x)=P_max-P_{rz}\geqslant 0\)
-
\(g_4(x)=P_max v_{vrmax}-P_{rz}v_{sr}\geqslant 0\)
-
\(g_5(x)=v_{srmax}-v_{sr}\geqslant 0\)
-
\(g_6(x)=T_max-T\geqslant 0\)
-
\(g_7(x)=M_h-sM_s\geqslant 0\)
-
\(g_8(x)=T\geqslant 0\)
-
where
-
\(M_h=\frac{2}{3}\mu FZ\frac{r_0^3-r_i^3}{r_0^2-r_i^2}\)
-
\(P_{rz}=\frac{2}{3}\frac{F}{\pi (r_0^2-r_i^2)}\)
-
\(v_{rz}=\frac{2\pi n (r_0^3-r_i^3)}{90(r_0^3-r_i^3)}\)
-
\(T = \frac{I_z\pi n}{30(M_h-M_f)}\)
-
\(\Delta r=20mm, I_z=55kgm^2, P_max=1MPa, F_max=1000N, T_max=15s,\mu =0.5\)
-
\(s=1.5, M_s=40Nm, M_f=3Nm, n=250r/min, v_{srmax}=10m/s, l_{max}=30mm\)
-
\(60mm\le r_i\le 80mm, 90mm\le r_0\le , 110mm, 1.5mm\le t \le 3mm,600N\le F\le 1000N, 2 \le Z \le 9 \)
E: Speed reducer design problem
-
\( Minimize(f(x))=0.7854x_1x_2^2(3.3333x_3^2+14.9334x_3-43.0934)-1.508x_1(x_6^2+x_7^2)+7.4777(x_6^3+x_7^3)+0.7854(x_4x_6^2+x_5x_7^2)\)
-
s.t;
-
\(g_1(x)=\frac{27}{x_1x_2^2x_3}-1\le 0\)
-
\(g_2(x)=\frac{397.5}{x_1x_2^2x_3^2}-1\le 0\)
-
\(g_3(x)=\frac{1.93x_4^3}{x_2x_6^4x_3}-1\le 0\)
-
\(g_4(x)=\frac{1.93x_5^3}{x_2x_7^4x_3}-1\le 0\)
-
\(g_5(x)=\frac{[(745x_4/x_2x_3)^2+16.9 \times 10^6]^0.5}{110x_6^3}-1\le 0\)
-
\(g_6(x)=\frac{[(745x_5/x_2x_3)^2+157.5 \times 10^6]^0.5}{85x_7^3}-1\le 0\)
-
\(g_7(x)=x_2x_3/40-1\le 0\)
-
\(g_8(x)=\frac{5x_2}{x_1}-1\le 0\)
-
\(g_9(x)=\frac{x_1}{12x_2}-1\le 0\)
-
\(g_10(x)=\frac{1.5x_6+1.9}{x_4}-1\le 0\)
-
\(g_11(x)=\frac{1.1x_7+1.9}{x_5}-1\le 0\)
-
where
-
\(2.6\le x_1\le , 0.7\le x_2\le 0.8, 17\le x_3 \le 28, 7.3\le x_4 \le 8.3, 7.3\le x_5\le 8.3\)
-
\(2.9\le x_6\le 3.9, 5.0\le x_7\le 5.5 \)
Rights and permissions
About this article
Cite this article
Singh, N., Kaur, J. Hybridizing sine–cosine algorithm with harmony search strategy for optimization design problems. Soft Comput 25, 11053–11075 (2021). https://doi.org/10.1007/s00500-021-05841-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-021-05841-y