Analysis of $$MAP, PH_{2}^{OA}/PH_{1}^{I}, PH_{2}^{O}/1$$ retrial queue with vacation, feedback, two-way communication and impatient customers | Soft Computing Skip to main content
Springer Nature Link
Log in

Analysis of \(MAP, PH_{2}^{OA}/PH_{1}^{I}, PH_{2}^{O}/1\) retrial queue with vacation, feedback, two-way communication and impatient customers

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

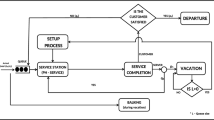
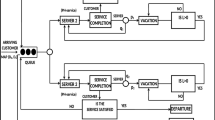
Abstract

This article concentrates on the steady-state analysis of a constant retrial queueing system with impatient customers, vacation, feedback, and two types of arrivals, namely the incoming calls which are made by the customers and the outgoing calls which are made by the server during the idle period. The incoming calls arrive at the system by following the Markovian Arrival Process(MAP) and service times of incoming/outgoing calls follow phase-type (PH) distribution, and the rest of the random variables are exponentially distributed. We have framed our model for analyzing some of the basic situations/problems in telecommunication systems. With the support of matrix analytic method, the invariant analysis of our system has been carried out. We have also discussed the busy period and have performed the cost analysis for our model. At last, we have validated our model through numerical and graphical exemplifications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40
Fig. 41
Fig. 42
Fig. 43
Fig. 44
Fig. 45
Fig. 46
Fig. 47
Fig. 48
Fig. 49

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Pondicherry Engineering College, Pillaichavady, Puducherry, India

    G. Ayyappan & R. Gowthami

Authors
  1. G. Ayyappan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. R. Gowthami
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to R. Gowthami.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the author.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ayyappan, G., Gowthami, R. Analysis of \(MAP, PH_{2}^{OA}/PH_{1}^{I}, PH_{2}^{O}/1\) retrial queue with vacation, feedback, two-way communication and impatient customers. Soft Comput 25, 9811–9838 (2021). https://doi.org/10.1007/s00500-020-05318-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-020-05318-4

Keywords