Applications of contractive-like mapping principles to fuzzy fractional integral equations with the kernel $$\psi $$ -functions | Soft Computing Skip to main content
Springer Nature Link
Log in

Applications of contractive-like mapping principles to fuzzy fractional integral equations with the kernel \(\psi \)-functions

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

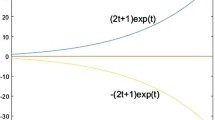
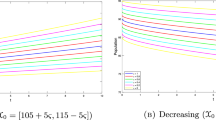
Abstract

In this work, we present a new class of generalized fractional integral equations with respect to the kernel \(\psi \)-function under the fuzzy concept. The results of this problem can be used to recover a wide class of fuzzy fractional integral equations by the choice of the kernel \(\psi \)-function. Without the Lipschitzian right-hand side, we investigate the existence and uniqueness of the fuzzy solutions by employing the fixed point theorem of weakly contractive mappings in the partially ordered space of fuzzy numbers. The proposed approach is based on the concept of a fuzzy metric space endowed with a partial order and the altering distance functions. In addition, the continuous dependence of solutions on the order and the initial condition of the given problem is also shown. Some concrete examples are presented in order to consolidate the obtained result.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Agarwal RP, Lakshmikantham V, Nieto JJ (2010) On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal Theory Methods Appl 72:2859–2862

    MathSciNet  MATH  Google Scholar 

  • Agarwal RP, Arshad S, O’Regan D, Lupulescu V (2012) Fuzzy fractional integral equations under compactness type condition. Fract Calc Appl Anal 15:572–590

    MathSciNet  MATH  Google Scholar 

  • Ahmadian A, Salahshour S, Chan CS (2017a) Fractional differential systems: a fuzzy solution based on operational matrix of shifted Chebyshev polynomials and its applications. IEEE Trans Fuzzy Syst 25:218–236

    Google Scholar 

  • Ahmadian A, Ismail F, Salahshour S, Baleanu D, Ghaemi F (2017b) Uncertain viscoelastic models with fractional order: a new spectral tau method to study the numerical simulations of the solution. Commun Nonlinear Sci Numer Simul 53:44–64

    MathSciNet  MATH  Google Scholar 

  • Alikhani R, Bahrami F (2013) Global solutions for nonlinear fuzzy fractional integral and integro-differential equations. Commun Nonlinear Sci Numer Simul 18:2007–2017

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T, Salahshour S, Abbasbandy S (2012a) Explicit solutions of fractional differential equations with uncertainty. Soft Comput 16:297–302

    MATH  Google Scholar 

  • Allahviranloo T, Salahshour S, Abbasbandy S (2012b) Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun Nonlinear Sci Numer Simul 17:1372–1381

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T, Gouyandeh Z, Armand A (2014) Fuzzy fractional differential equations under generalized fuzzy Caputo derivative. J Intell Fuzzy Syst 26:1481–1490

    MathSciNet  MATH  Google Scholar 

  • Almeida R (2017) A Caputo fractional derivative of a function with respect to another function. Commun Nonlinear Sci Numer Simul 44:460–481

    MathSciNet  MATH  Google Scholar 

  • An TV, Vu H, Hoa NV (2017a) Applications of contractive-like mapping principles to interval-valued fractional integro-differential equations. J Fixed Point Theory Appl 19:2577–99

    MathSciNet  MATH  Google Scholar 

  • An TV, Vu H, Hoa NV (2017) A new technique to solve the initial value problems for fractional fuzzy delay differential equations. Adv Differ Equ 2017:181

    MathSciNet  MATH  Google Scholar 

  • Arshad S, Lupulescu V (2011) On the fractional differential equations with uncertainty. Nonlinear Anal Theory Appl 7:85–93

    MATH  Google Scholar 

  • Bede B, Gal SG (2005) Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst 151:581–599

    MathSciNet  MATH  Google Scholar 

  • Bede B, Stefanini L (2013) Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst 230:119–141

    MathSciNet  MATH  Google Scholar 

  • Fard OS, Salehi M (2014) A survey on fuzzy fractional variational problems. J Comput Appl Math 271:71–82

    MathSciNet  MATH  Google Scholar 

  • Harjani J, Sadarangani K (2010) Generalized contractions in partially ordered metric spaces and applications to ordinary differential equations. Nonlinear Anal 72:1188–1197

    MathSciNet  MATH  Google Scholar 

  • Hoa NV (2015a) Fuzzy fractional functional integral and differential equations. Fuzzy Sets Syst 280:58–90

    MathSciNet  MATH  Google Scholar 

  • Hoa NV (2015b) Fuzzy fractional functional differential equations under Caputo gH-differentiability. Commun Nonlinear Sci Numer Simul 22:1134–1157

    MathSciNet  MATH  Google Scholar 

  • Hoa NV (2020) On the initial value problem for fuzzy differential equations of non-integer order \(\alpha \in (1, 2) \). Soft Comput 24(2):935–954

    MATH  Google Scholar 

  • Hoa NV, Ho V (2019) A survey on the initial value problems of fuzzy implicit fractional differential equations. Fuzzy Sets Syst. https://doi.org/10.1016/j.fss.2019.10.012

    Article  Google Scholar 

  • Hoa NV, Lupulescu V, O’Regan D (2017) Solving interval-valued fractional initial value problem under Caputo gH-fractional differentiability. Fuzzy Sets Syst 309:1–34

    MathSciNet  MATH  Google Scholar 

  • Hoa NV, Lupulescu V, O’Regan D (2018) A note on initial value problems for fractional fuzzy differential equations. Fuzzy Sets Syst 347:54–69

    MathSciNet  MATH  Google Scholar 

  • Hoa NV, Vu H, Duc TM (2019) Fuzzy fractional differential equations under Caputo–Katugampola fractional derivative approach. Fuzzy Sets Syst 375:70–99

    MathSciNet  MATH  Google Scholar 

  • Khastan A, Nieto JJ, Rodríguez-López R (2014) Fuzzy delay differential equations under generalized differentiability. Inf Sci 275:145–67

    MathSciNet  MATH  Google Scholar 

  • Long HV, Son NTK, Hoa NV (2017a) Fuzzy fractional partial differential equations in partially ordered metric spaces. Iran J Fuzzy Syst 14:107–126

    MathSciNet  MATH  Google Scholar 

  • Long HV, Son NTK, Tam HTT, Yao JC (2017b) Ulam stability for fractional partial integro-differential equation with uncertainty. Acta Math Vietnam 42:675–700

    MathSciNet  MATH  Google Scholar 

  • Long HV, Son NK, Tam HT (2017c) The solvability of fuzzy fractional partial differential equations under Caputo gH-differentiability. Fuzzy Sets Syst 309:35–63

    MathSciNet  MATH  Google Scholar 

  • Long HV, Nieto JJ, Son NTK (2018) New approach for studying nonlocal problems related to differential systems and partial differential equations in generalized fuzzy metric spaces. Fuzzy Sets Syst 331:26–46

    MathSciNet  MATH  Google Scholar 

  • Lupulescu V (2015) Fractional calculus for interval-valued functions. Fuzzy Sets Syst 265:63–85

    MathSciNet  MATH  Google Scholar 

  • Lupulescu V, Hoa NV (2017) Interval Abel integral equation. Soft Comput 21:2777–2784

    MATH  Google Scholar 

  • Malinowski MT (2015) Random fuzzy fractional integral equations-theoretical foundations. Fuzzy Sets Syst 265:39–62

    MathSciNet  MATH  Google Scholar 

  • Mazandarani M, Kamyad AV (2013) Modified fractional Euler method for solving fuzzy fractional initial value problem. Commun Nonlinear Sci Numer Simul 18:12–21

    MathSciNet  MATH  Google Scholar 

  • Mazandarani M, Najariyan M (2014) Type-2 fuzzy fractional derivatives. Commun Nonlinear Sci Numer Simul 19:2354–2372

    MathSciNet  MATH  Google Scholar 

  • Nieto JJ, Rodríguez-López R (2005) Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 22:223–239

    MathSciNet  MATH  Google Scholar 

  • Nieto JJ, Rodríguez-López R (2007) Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Math Sin 23:2205–2212

    MathSciNet  MATH  Google Scholar 

  • Noeiaghdam Z, Allahviranloo T, Nieto JJ (2019) \(q-\)fractional differential equations with uncertainty. Soft Comput 23:9507–9524

    MATH  Google Scholar 

  • Quang LTQ, Hoa NV, Phu ND, Tung TT (2016) Existence of extremal solutions for interval-valued functional integro-differential equations. J Intell Fuzzy Syst 30:3495–3512

    MATH  Google Scholar 

  • Ran ACM, Reurings MCB (2004) A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc Am Math Soc 132:1435–1443

    MathSciNet  MATH  Google Scholar 

  • Rodríguez-López R (2008) Monotone method for fuzzy differential equations. Fuzzy Sets Syst 159:2047–76

    MathSciNet  MATH  Google Scholar 

  • Salahshour S, Allahviranloo T, Abbasbandy S (2012) Solving fuzzy fractional differentialequations by fuzzy Laplace transforms. Commun Nonlinear Sci Numer Simul 17:1372–1381

    MathSciNet  MATH  Google Scholar 

  • Salahshour S, Ahmadian A, Senu N, Baleanu D, Agarwal P (2015) On analytical solutions of the fractional differential equation with uncertainty: application to the Basset problem. Entropy 17:885–902

    MathSciNet  MATH  Google Scholar 

  • Sousa JVC, de Oliveira EC (2019) A Gronwall inequality and the Cauchy-type problem by means of \(\psi \)-Hilfer operator. Differ Equ Appl 11:87–106

    MathSciNet  MATH  Google Scholar 

  • Stefanini L (2010) A generalization of Hukuhara difference and division for interval and fuzzy arithmetic. Fuzzy Sets Syst 161:1564–1584

    MathSciNet  MATH  Google Scholar 

  • Villamizar-Roa EJ, Angulo-Castillo V, Chalco-Cano Y (2015) Existence of solutions to fuzzy differential equations with generalized Hukuhara derivative via contractive-like mapping principles. Fuzzy Sets Syst 265:24–38

    MathSciNet  MATH  Google Scholar 

  • Vu H, An TV, Van Hoa N (2020) Ulam-Hyers stability of uncertain functional differential equation in fuzzy setting with Caputo-Hadamard fractional derivative concept. J Intell Fuzzy Syst 38(2):2245–2259. https://doi.org/10.3233/JIFS-191025

    Article  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the referees for their valuable suggestions, which helped to improve the paper significantly.

Author information

Authors and Affiliations

  1. Institute of Research and Development, Duy Tan University, Danang, 550000, Vietnam

    Ho Vu

  2. Faculty of Natural Sciences, Duy Tan University, Danang, 550000, Vietnam

    Ho Vu

  3. Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Ngo Van Hoa

  4. Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Ngo Van Hoa

Authors
  1. Ho Vu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ngo Van Hoa
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ngo Van Hoa.

Ethics declarations

Conflict of interest

The authors declare that they has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Communicated by V. Loia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vu, H., Van Hoa, N. Applications of contractive-like mapping principles to fuzzy fractional integral equations with the kernel \(\psi \)-functions . Soft Comput 24, 18841–18855 (2020). https://doi.org/10.1007/s00500-020-05115-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-020-05115-z

Keywords