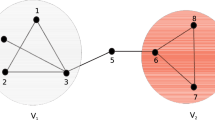
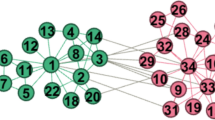
Abstract
Noisy extremal optimization is a new optimization-based heuristic designed to identify the community structure of complex networks by maximizing the modularity function. The extremal optimization algorithm evolves configurations that represent network covers, composed of nodes evaluated separately. Each iteration, a number of nodes having the worst fitness values are randomly assigned different communities. A network shifting procedure is used to induce a noise in the population as a diversity preserving mechanism. Numerical experiments, performed on synthetic and real-world networks, illustrate the potential of this approach.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
Using the code available at https://sites.google.com/site/andrealancichinetti/software.
http://www.orgnet.com, last accessed 9/3/2015.
See footnote 1.
By using the source code available at https://sites.google.com/site/andrealancichinetti/software.
References
Amiri B, Hossain L, Crawford JW, Wigand RT (2013) Community detection in complex networks. Knowl Based Syst 46:1–11
Boettcher S, Percus A (2000) Nature’s way of optimizing. Artif Intell 119(1):275–286
Boettcher S, Percus AG (2001) Optimization with extremal dynamics. Phys Rev Lett 86:5211–5214
Boettcher S, Percus AG (2003) Extremal optimization: an evolutionary local-search algorithm. In: Computational modeling and problem solving in the networked world. Springer US, pp 61–77
Duch J, Arenas A (2005) Community detection in complex networks using extremal optimization. Phys Rev E 72:027104
Folino F, Pizzuti C (2014) An evolutionary multiobjective approach for community discovery in dynamic networks. IEEE Trans Knowl Data Eng 26(8):1–1
Fortunato S (2010) Community detection in graphs. Phys Rep 486(3):75–174
Fortunato S, Barthelemy M (2007) Resolution limit in community detection. Proc Natl Acad Sci 104(1):36–41
Girvan M, Newman MEJ (2002) Community structure in social and biological networks. Proc Natl Acad Sci 99(12):7821–7826
Gong M, Fu B, Jiao L, Du H (2011) Memetic algorithm for community detection in networks. Phys Rev E 84:056101
Gong M, Ma L, Zhang Q, Jiao L (2012) Community detection in networks by using multiobjective evolutionary algorithm with decomposition. Phys A 391(15):4050–4060
Gong M, Cai Q, Chen X, Ma L (2014a) Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition. IEEE Trans Evol Comput 18(1):82–97
Gong M, Liu J, Ma L, Cai Q, Jiao L (2014b) Novel heuristic density-based method for community detection in networks. Phys A 403:71–84
Grappiolo C, Togelius J, Yannakakis GN (2013) Shifting niches for community structure detection. In: 2013 IEEE congress on evolutionary computation (CEC), pp 111–118. IEEE
Honghao C, Zuren F, Zhigang R (2013) Community detection using ant colony optimization. In: 2013 IEEE congress on evolutionary computation (CEC), pp 3072–3078
Jiang JQ, McQuay LJ (2012) Modularity functions maximization with nonnegative relaxation facilitates community detection in networks. Phys A 391(3):854–865
Lancichinetti A, Fortunato S (2009) Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys Rev E 80:016118
Lancichinetti A, Fortunato S, Kertész J (2009) Detecting the overlapping and hierarchical community structure in complex networks. New J Phys 11(3):033015
Lancichinetti A, Radicchi F, Ramasco JJ, Fortunato S (2011) Finding statistically significant communities in networks. PloS One 6(4):e18961
Li Z, Zhang S, Wang R-S, Zhang X-S, Chen Luonan (2008) Quantitative function for community detection. Phys Rev E 77:036109
Lung RI, Chira C, Andreica A (2014) Game theory and extremal optimization for community detection in complex dynamic networks. PLoS One 9(2):e86891, 02
Lung RI, Gog A, Chira C (2011) A game theoretic approach to community detection in social networks. In: Nature inspired cooperative strategies for optimization, NICSO 2011, Cluj-Napoca, Romania October 20–22 (2011), pp 121–131
Lusseau D, Schneider K, Boisseau OJ, Haase P, Slooten Elisabeth, Dawson SteveM (2003) The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations. Behav Ecol Sociobiol 54(4):396–405
Nascimento MCV, Pitsoulis L (2013) Community detection by modularity maximization using GRASP with path relinking. Comput Oper Res 40(12):3121–3131
Newman MEJ (2006) Modularity and community structure in networks. Proc Natl Acad Sci 103(23):8577–8582
Newman MEJ (2013) Spectral methods for community detection and graph partitioning. Phys Rev E 88(4):042822
Newman MEJ, Girvan M (2004) Finding and evaluating community structure in networks. Phys Rev E 69(2):026113
Pizzuti C (2008) Ga-net: a genetic algorithm for community detection in social networks. Parallel problem solving from nature–PPSN X. Springer, Berlin, pp 1081–1090
Pizzuti C (2012) A multiobjective genetic algorithm to find communities in complex networks. IEEE Trans Evol Comput 16(3):418–430
Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc Natl Acad Sci 105(4):1118–1123
Sales-Pardo M, Guimerà R, Moreira AA, Amaral LAN (2007) Extracting the hierarchical organization of complex systems. Proc Natl Acad Sci 104(39):15224–15229
Shang R, Bai J, Jiao L, Jin C (2013) Community detection based on modularity and an improved genetic algorithm. Phys A 392(5):1215–1231
Shen HW, Cheng XQ (2010) Spectral methods for the detection of network community structure: a comparative analysis. J Stat Mech 2010(10):P10020
Shi C, Yan Z, Cai Y, Bin W (2012) Multi-objective community detection in complex networks. Appl Soft Comput 12(2):850–859
Zachary WW (1977) An information flow model for conflict and fission in small groups. J Anthropol Res 33(4):452–473
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Communicated by V. Loia.
Appendix
Appendix
The appendix contains supplementary numerical results and graphics with results.
See Figs. 8, 9, and 10 and Tables 1, 2, 3, 4, 5, 6 and 7.
NoisyEO: results obtained for different parameter settings; for each network, top figure represents the best NMI in the population; in the bottom the NMI of the individual having the best modularity; parameter settings: same as Fig. 8
Rights and permissions
About this article
Cite this article
Lung, R.I., Suciu, M. & Gaskó, N. Noisy extremal optimization. Soft Comput 21, 1253–1270 (2017). https://doi.org/10.1007/s00500-015-1858-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-015-1858-3