Some Graphs with Double Domination Subdivision Number Three | Graphs and Combinatorics Skip to main content
Springer Nature Link
Log in

Some Graphs with Double Domination Subdivision Number Three

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

An Erratum to this article was published on 29 January 2013

Abstract

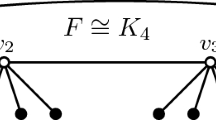
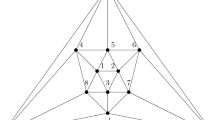
A subset \({S \subseteq V(G)}\) is a double dominating set of G if S dominates every vertex of G at least twice. The double domination number dd(G) is the minimum cardinality of a double dominating set of G. The double domination subdivision number sd dd (G) is the minimum number of edges that must be subdivided (where each edge in G can be subdivided at most once) in order to increase the double domination number. Atapour et al. (Discret Appl Math, 155:1700–1707, 2007) posed an open problem: Prove or disprove: let G be a connected graph with no isolated vertices, then 1 ≤ sd dd (G) ≤ 2. In this paper, we disprove the problem by constructing some connected graphs with no isolated vertices and double domination subdivision number three.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Atapour M., Khodkar A., Sheikholeslami S.M.: Characterization of double domination subdivision number of trees. Discret. Appl. Math 155, 1700–1707 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  2. Favaron O., Haynes T.W., Hedetniemi S.T.: Domination subdivision numbers in graphs. Util. Math. 66, 195–209 (2004)

    MATH  MathSciNet  Google Scholar 

  3. Favaron O., Karami H., Sheikholeslami S.M.: Disproof of a conjecture on the subdivision domination number of a graph. Graphs Combin. 24, 309–312 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  4. Harary F., Haynes T.W.: Double domination in graphs. Ars Combin. 55, 201–213 (2000)

    MATH  MathSciNet  Google Scholar 

  5. Haynes T.W., Hedetniemi S.M., Hedetniemi S.T., Knisely J., van der Merwe L.C: Domination subdivision numbers. Discuss. Math. Graph Theory 21, 239–253 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  6. Haynes, T.W., Hedetniemi, S.T., Slater, P.J.: Fundamentals of Domination in Graphs. Marcel Dekker, Inc. NewYork (1998)

Download references

Author information

Authors and Affiliations

  1. College of Computer and Information Engineering, Tianjin Normal University, Tianjin, 300387, China

    Haoli Wang

  2. Department of Computer Science, Dalian University of Technology, Dalian, 116024, China

    Xirong Xu, Yuansheng Yang & Baosheng Zhang

Authors
  1. Haoli Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xirong Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuansheng Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Baosheng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuansheng Yang.

Additional information

The research is supported by Chinese Natural Science Foundations (60973014, 61170303).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, H., Xu, X., Yang, Y. et al. Some Graphs with Double Domination Subdivision Number Three. Graphs and Combinatorics 30, 247–251 (2014). https://doi.org/10.1007/s00373-012-1254-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-012-1254-z

Keywords

Search

Navigation