Abstract
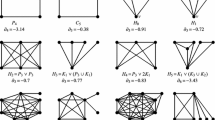
A friendship graph is a graph in which every two distinct vertices have exactly one common neighbor. All finite friendship graphs are known, each of them consists of triangles having a common vertex. We extend friendship graphs to two-graphs, a two-graph being an ordered pair G = (G 0, G 1) of edge-disjoint graphs G 0 and G 1 on the same vertex-set V(G 0) = V(G 1). One may think that the edges of G are colored with colors 0 and 1. In a friendship two-graph, every unordered pair of distinct vertices u, v is connected by a unique bicolored 2-path. The pairs of adjacency matrices of friendship two-graphs are solutions to the matrix equation AB + BA = J − I, where A and B are n × n symmetric 0 − 1 matrices, J is an n × n matrix with every entry being 1, and I is the identity n × n matrix. We show that there is no finite friendship two-graph with minimum vertex degree at most two. However, we construct an infinite such graph, and this construction can be extended to an infinite (uncountable) family. Also, we find a finite friendship two-graph, conjecture that it is unique, and prove this conjecture for the two-graphs that have a dominating vertex.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bondy, J.A.: Kotzig’s conjecture on generalized friendship graphs—a survey. In: Cycles in Graphs (Burnaby, B.C., 1982). North-Holland Math. Stud., vol. 115, pp. 351–366. North-Holland, Amsterdam (1985)
Boros E., Gurvich V.: Vertex- and edge-minimal and locally minimal graphs. Discrete Math. 309(12), 3853–3865 (2009)
Chvátal V., Graham R.L., Perold A.F., Whitesides S.H.: Combinatorial designs related to the strong perfect graph conjecture. Discrete Math. 26(2), 83–92 (1979)
Erdős P., Rényi A., Sós V.T.: On a problem of graph theory. Studia Sci. Math. Hungar. 1, 215–235 (1966)
Gurvich V.: Some properties and applications of complete edge-chromatic graphs and hypergraphs. Soviet Math. Dokl. 30(3), 803–807 (1984)
Gurvich V.: Decomposing complete edge-chromatic graphs and hypergraphs. Revisited, Discrete Appl. Math. 157, 3069–3085 (2009)
Kostochka A.V.: The nonexistence of certain generalized friendship graphs. In: Combinatorics (Eger, 1987). Colloq. Math. Soc. János Bolyai, vol. 52. North-Holland, Amsterdam (1988)
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was partially supported by DIMACS, Center for Discrete Mathematics and Theoretical Computer Science, Rutgers University, and by Graduate School of Information Science and Technology, University of Tokyo.
Rights and permissions
About this article
Cite this article
Boros, E., Gurvich, V.A. & Zverovich, I.E. Friendship Two-Graphs. Graphs and Combinatorics 26, 617–628 (2010). https://doi.org/10.1007/s00373-010-0914-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00373-010-0914-0