Abstract
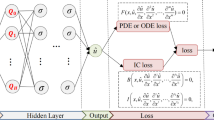
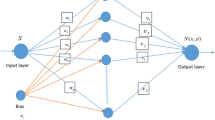
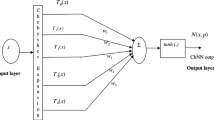
In this paper, we propose an Artificial Neural Network (ANN) method for solving some well-known classes of Lane–Emden type equations which are the important nonlinear singular second order differential equations. In this method, we introduced Legendre and Chebyshev blocks as a new efficient neural network architecture based on mathematical properties of Jacobi polynomials to approximate the solution of nonlinear differential equations. The operational matrix in the back-propagation phase is used to calculate the gradient of the cost function according to the network weights, therefor the computations of this architecture are reduced. In order to determine the effect of Legender and Chebyshev blocks, two similar models were built, one using these blocks as activation functions and one without them. Comparing these two models on different examples shows that these blocks significantly increase the accuracy. Also we compared the present work with some well-known approximate results in several examples, revealing that the proposed architecture is effective and accurate.




Similar content being viewed by others
References
Abbas Fazal et al. (2020) “Analytical Approach to Study the Generalized Lane-Emden Model Arises in the Study of Stellar Configuration”. In: Applied Mathematics & Information Sciences. 14(3), 355-364
Ahmad Iftikhar et al. (2016) “Bio-inspired computational heuristics to study Lane-Emden systems arising in astrophysics model”. In: SpringerPlus. 5(1), 1-23
Alomari AK, Alshbail Abdallah (2018) “Modified Legendre operator matrix for nonlinear IVP”. In: AIP Conference Proceedings. Vol. 1978. 1. AIP Publishing LLC. 050003.1-050003.4
Soner Aydinlik and A Kiris. “First order smooth composite Chebyshev finite difference method for solving coupled Lane-Emden problem in catalytic diffusion reactions”. In: MATCH Commun. Math. Comput. Chem 87 (2022), pp. 463-476
Aydinlik S, Kiris A, Roul P (2022) An effective approach based on Smooth Composite Chebyshev Finite Difference Method and its applications to Bratu-type and higher order Lane-Emden problems. Math Comput Simul 202:193–205
Yosry Azzam, Emad A-B Abdel-Salam, Mohamed I Nouh, et al (2021) “Artificial neural network modeling of the conformable fractional isothermal gas spheres”. In: Revista mexicana de astronomía y astrofísica. 57(1), 189-198
Ali H Bhrawy and Abdulaziz S Alofi. “A Jacobi-Gauss collocation method for solving nonlinear Lane-Emden type equations”. In: Communications in Nonlinear Science and Numerical Simulation 17.1 (2012), pp. 62-70
John P Boyd. “Chebyshev spectral methods and the Lane-Emden problem”. In: Numerical Mathematics: Theory, Methods and Applications 4.2 (2011), pp. 142-157
Snehashish Chakraverty and Susmita Mall. Artificial neural networks for engineers and scientists: solving ordinary differential equations. CRC Press, 2017
Po L Chambré. “On the solution of the Poisson-Boltzmann equation with application to the theory of thermal explosions”. In: The Journal of Chemical Physics 20.11 (1952), pp. 1795-1797
Subrahmanyan Chandrasekhar. An introduction to the study of stellar structure. Vol. 2. Courier Corporation, 1957
Michael Chapwanya, Robert Dozva, and Gift Muchatibaya. “A nonstandard finite difference technique for singular Lane-Emden type equations”. In: Engineering Computations 36.5 (2019), pp. 1566-1578
MSH Chowdhury and Ishak Hashim. “Solutions of a class of singular second-order IVPs by homotopy-perturbation method”. In: Physics Letters A 365.5-6 (2007), pp. 439-447
MSH Chowdhury and Ishak Hashim. “Solutions of Emden-Fowler equations by homotopyperturbation method”. In: Nonlinear Analysis: Real World Applications 10.1 (2009), pp. 104- 115
Harold Thayer Davis. Introduction to nonlinear differential and integral equations. US Atomic Energy Commission, 1960
Dehghan M, Shakeri F (2008) Solution of an integro-differential equation arising in oscillating magnetic fields using He’s homotopy perturbation method. Progress in Electromagnetics Research 78:361–376
RW Dickey. “Rotationally symmetric solutions for shallow membrane caps”. In: Quarterly of Applied Mathematics 47.3 (1989), pp. 571-581
A Karimi Dizicheh et al. “A novel algorithm based on the Legendre wavelets spectral technique for solving the Lane-Emden equations”. In: Applied Numerical Mathematics 153 (2020), pp. 443- 456
RC Duggan and AM Goodman. “Pointwise bounds for a nonlinear heat conduction model of the human head”. In: Bulletin of mathematical biology 48.2 (1986), pp. 229-236
Kareem T Elgindy and Hareth M Refat. “High-order shifted Gegenbauer integral pseudo-spectral method for solving differential equations of Lane-Emden type”. In: Applied Numerical Mathematics 128 (2018), pp. 98-124
R Emden. “Gaskugeln Anwendungen der Mechan”. In: Warmtheorie. Teubner, Leipzig/Berlin (1907)
Vedat Suat Ertürk. “Differential transformation method for solving differential equations of Lane- Emden type”. In: Mathematical and computational Applications 12.3 (2007), pp. 135-139
Gümgüm S (2020) Taylor wavelet solution of linear and nonlinear Lane-Emden equations. Appl Numer Math 158:44–53
Amir Hosein Hadian-Rasanan et al. “A single layer fractional orthogonal neural network for solving various types of Lane-Emden equation”. In: New Astronomy 75 (2020), pp. 101307.1- 101307.14
Z Hajimohammadi, S Shekarpaz, and Kourosh Parand. “The novel learning solutions to nonlinear differential models on a semi-infinite domain”. In: Engineering with Computers (2022), pp. 1-18
Mir Sajjad Hashemi et al. “Solving the Lane-Emden Equation within a Reproducing Kernel Method and Group Preserving Scheme”. In: Mathematics 5.4 (2017)
Ji-Huan He. “Variational approach to the Lane-Emden equation”. In: Applied Mathematics and Computation 143.2-3 (2003), pp. 539-541
Ji-Huan He and Fei-Yu Ji. “Taylor series solution for Lane-Emden equation”. In: Journal of Mathematical Chemistry 57.8 (2019), pp. 1932-1934
S Gh Hosseini and S Abbasbandy. “Solution of Lane-Emden type equations by combination of the spectral method and Adomian decomposition method”. In: Mathematical Problems in Engineering 2015 (2015), pp. 534754.1 -534754.10
ASV Ravi Kanth and K Aruna. “He’s variational iteration method for treating nonlinear singular boundary value problems”. In: Computers & Mathematics with Applications 60.3 (2010), pp. 821- 829
Junaid Ali Khan et al. “Nature-inspired computing approach for solving non-linear singular Emden-Fowler problem arising in electromagnetic theory”. In: Connection Science 27.4 (2015), pp. 377-396
Najeeb Alam Khan and Amber Shaikh. “A smart amalgamation of spectral neural algorithm for nonlinear Lane-Emden equations with simulated annealing”. In: Journal of Artificial Intelligence and Soft Computing Research 7.3 (), pp. 215-224
Yasir Khan, Zdeněk Svoboda, and Zdeněk Šmarda. “Solving certain classes of Lane-Emden type equations using the differential transformation method”. In: Advances in difference equations 2012.1 (2012), pp. 1-11
Homer J. Lane. “On the theoretical temperature of the Sun, under the hypothesis of a gaseous mass maintaining its volume by its internal heat, and depending on the laws of gases as known to terrestrial experiment”. In: American Journal of Science and Arts s2-50 (1870), pp. 57 -74
Shijun Liao. “A new analytic algorithm of Lane-Emden type equations”. In: Applied Mathematics and Computation 142.1 (2003), pp. 1-16
Tao Luo, Zhouping Xin, and Huihui Zeng. “Nonlinear asymptotic stability of the Lane-Emden solutions for the viscous gaseous star problem with degenerate density dependent viscosities”. In: Communications in Mathematical Physics 347.3 (2016), pp. 657-702
Susmita Mall and S Chakraverty. “A novel Chebyshev neural network approach for solving singular arbitrary order Lane-Emden equation arising in astrophysics”. In: Network: Computation in Neural Systems 31.1-4 (2020), pp. 142-165
Susmita Mall, Sumit Kumar Jeswal, and Snehashish Chakraverty. “Connectionist Learning Models for Application Problems Involving Differential and Integral Equations”. In: Mathematical Methods in Interdisciplinary Sciences (2020), pp. 1-22
VB Mandelzweig and F Tabakin. “Quasilinearization approach to nonlinear problems in physics with application to nonlinear ODEs”. In: Computer Physics Communications 141.2 (2001), pp. 268-281
M Merafina, GS Bisnovatyi-Kogan, and SO Tarasov. “A brief analysis of self-gravitating polytropic models with a non-zero cosmological constant”. In: Astronomy & Astrophysics 541.A84 (2012), pp. 1 -5
Babur M Mirza. “Approximate analytical solutions of the Lane-Emden equation for a selfgravitatingisothermal gas sphere”. In: Monthly Notices of the Royal Astronomical Society 395.4 (2009), pp. 2288-2291
Ben Muatjetjeja and Chaudry Masood Khalique. “Noether, partial Noether operators and first integrals for the coupled Lane-Emden system”. In: Mathematical and Computational Applications 15.3 (2010), pp. 325-333
Supriya Mukherjee, Banamali Roy, and Pratik Kumar Chaterjee. “Solution of Lane-Emden equation by differential transform method”. In: International Journal of Nonlinear Science 12.4 (2011), pp. 478-484
MO Ogunniran et al. “Linear stability analysis of Runge-Kutta methods for singular Lane-Emden equations”. In: Journal of the Nigerian Society of Physical Sciences (2020), pp. 134-140
Rajesh K Pandey and Narayan Kumar. “Solution of Lane-Emden type equations using Bernstein operational matrix of differentiation”. In: New Astronomy 17.3 (2012), pp. 303-308
Rajesh K Pandey et al. “Solution of Lane-Emden type equations using Legendre operational matrix of differentiation”. In: Applied Mathematics and Computation 218.14 (2012), pp. 7629- 7637
Kourosh Parand and Soleiman Hashemi. “RBF-DQ method for solving non-linear differential equations of Lane-Emden type”. In: Ain Shams Engineering Journal 9.4 (2018), pp. 615-629
Kourosh Parand and Mohammad Hemami. “Numerical study of astrophysics equations by meshless collocation method based on compactly supported radial basis function”. In: International Journal of Applied and Computational Mathematics 3.2 (2017), pp. 1053-1075
Kourosh Parand, Mehran Nikarya, and Jamal Amani Rad. “Solving non-linear Lane-Emden type equations using Bessel orthogonal functions collocation method”. In: Celestial Mechanics and Dynamical Astronomy 116.1 (2013), pp. 97-107
Kourosh Parand and A Taghavi. “Generalized Laguerre polynomials collocation method for solving Lane-Emden equation”. In: Applied mathematical sciences 2.60 (2008), pp. 2955-2961
Parand K et al (2021) A new approach to the numerical solution of Fredholm integral equations using least squares-support vector regression. Math Comput Simul 180:114–128
Kourosh Parand et al. “An approximation algorithm for the solution of the nonlinear Lane- Emden type equations arising in astrophysics using Hermite functions collocation method”. In: Computer Physics Communications 181.6 (2010), pp. 1096-1108
Kourosh Parand et al. New Trends of Spectral Methods in Scientific Computing: Theory and Applications. Shahid Beheshti University, 2019. Chap. 2
Kourosh Parand et al. “Parallel LS-SVM for the numerical simulation of fractional Volterra’s population model”. In: Alexandria Engineering Journal 60.6 (2021), pp. 5637-5647
Juan I Ramos. “Linearization methods in classical and quantum mechanics”. In: Computer Physics Communications 153.2 (2003), pp. 199-208
Juan I Ramos. “Linearization techniques for singular initial-value problems of ordinary differential equations”. In: Applied Mathematics and Computation 161.2 (2005), pp. 525-542
Juan I Ramos. “Series approach to the Lane-Emden equation and comparison with the homotopy perturbation method”. In: Chaos, Solitons & Fractals 38.2 (2008), pp. 400-408
Sabir Z et al (2020) Novel design of Morlet wavelet neural network for solving second order Lane-Emden equation. Math Comput Simul 172:1–14
Bhuvnesh Sharma et al. “Chebyshev operational matrix method for Lane-Emden problem”. In: Nonlinear Engineering 8.1 (2019), pp. 1-9
NT Shawagfeh. “Nonperturbative approximate solution for Lane-Emden equation”. In: Journal of Mathematical Physics 34.9 (1993), pp. 4364-4369
Mandeep Singh and Amit K Verma. “An effective computational technique for a class of Lane- Emden equations”. In: Journal of Mathematical Chemistry 54.1 (2016), pp. 231-251
Om P Singh, Rajesh K Pandey, and Vineet K Singh. “An analytic algorithm of Lane-Emden type equations arising in astrophysics using modified homotopy analysis method”. In: Computer Physics Communications 180.7 (2009), pp. 1116-1124
Randhir Singh. “Optimal homotopy analysis method for the non-isothermal reaction-diffusionmodel equations in a spherical catalyst”. In: Journal of Mathematical Chemistry 56.9 (2018), pp. 2579- 2590
Muhammed I Syam et al. “An accurate method for solving a singular second-order fractional Emden-Fowler problem”. In: Advances in Difference Equations 2018.1 (2018), pp. 1-16
A Taghavi and S Pearce. “A solution to the Lane-Emden equation in the theory of stellar structure utilizing the Tau method”. In: Mathematical Methods in the Applied Sciences 36.10 (2013), pp. 1240-1247
Tsitouras Ch (2019) Explicit Runge-Kutta methods for starting integration of Lane-Emden problem. Appl Math Comput 354:353–364
Robert A Van Gorder and K Vajravelu. “Analytic and numerical solutions to the Lane-Emden equation”. In: Physics Letters A 372.39 (2008), pp. 6060-6065
Abdul-Majid Wazwaz. “A new algorithm for solving differential equations of Lane-Emden type”. In: Applied mathematics and computation 118(2-3) (2001), pp. 287-310
Abdul-Majid Wazwaz. “A new method for solving singular initial value problems in the secondorder ordinary differential equations”. In: Applied Mathematics and computation 128(1) (2002), pp. 45-57
Abdul-MajidWazwaz. “Solving the non-isothermal reaction-diffusion model equations in a spherical catalyst by the variational iteration method”. In: Chemical Physics Letters 679 (2017), pp. 132-136
Abdul-MajidWazwaz. “The modified decomposition method for analytic treatment of differential equations”. In: Applied mathematics and computation 173.1 (2006), pp. 165-176
Abdul-Majid Wazwaz and Randolph Rach. “Comparison of the Adomian decomposition method and the variational iteration method for solving the Lane-Emden equations of the first and second kinds”. In: Kybernetes (2011)
Ahmet Yıldırım and Turgut Öziş. “Solutions of singular IVPs of Lane-Emden type by the variational iteration method”. In: Nonlinear Analysis: Theory, Methods & Applications, 70(6) (2009), pp. 2480-2484
Sohrab Ali Yousefi. “Legendre wavelets method for solving differential equations of Lane-Emden type”. In: Applied Mathematics and Computation, 181(2) (2006), pp. 1417-1422
Zhu LD, Wang JH (1994) “The Formation and Propagation of a Shock Formed during the Gravitational Collapse of a Gaseous Polytrope”. In: Acta Astrophysica Sinica, 14(4) pp. 358- 366
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Parand, K., Aghaei, A.A., Kiani, S. et al. A neural network approach for solving nonlinear differential equations of Lane–Emden type. Engineering with Computers 40, 953–969 (2024). https://doi.org/10.1007/s00366-023-01836-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-023-01836-5