Numerical study of temperature distribution in an inverse moving boundary problem using a meshless method | Engineering with Computers Skip to main content
Springer Nature Link
Log in

Numerical study of temperature distribution in an inverse moving boundary problem using a meshless method

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

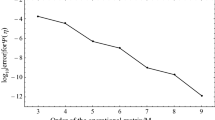
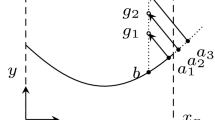
Abstract

In this paper, we consider the inverse one-phase one-dimensional Stefan problem to study the thermal processes with phase change in a moving boundary problem and calculate the temperature distribution in the given domain, as well as approximate the temperature and the heat flux on a boundary of the region. For this problem, the location of the moving boundary and temperature distribution on this curve are available as the extra specifications. First, we use the Landau’s transformation to get a rectangular domain and then apply the Crank–Nicolson finite-difference scheme to discretize the time dimension and reduce the problem to a linear system of differential equations. Next, we employ the radial basis function collocation technique to approximate the spatial unknown function and its derivatives at each time level. Finally, the linear systems of algebraic equations constructed in this way are solved using the LU factorization method. To show the numerical convergence and stability of the proposed method, we solve two benchmark examples when the boundary data are exact or contaminated with additive noises.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Abbasbandy S, Ghehsareh HR, Alhuthali MS, Alsulami HH (2014) Comparison of meshless local weak and strong forms based on particular solutions for a non-classical 2-D diffusion model. Eng Anal Bound Elem 39:121–128

    MathSciNet  MATH  Google Scholar 

  2. Abbasbandy S, Shirzadi A (2011) MLPG method for two-dimensional diffusion equation with Neumann’s and non-classical boundary conditions. Appl Numer Math 61:170–180

    MathSciNet  MATH  Google Scholar 

  3. Alexiades V, Solomon AD (1993) Mathematical modeling of melting and freezing processes. Hemisphere Publ. Corp, Washington

    Google Scholar 

  4. Assari P, Adibi H, Dehghan M (2013) A meshless method for solving nonlinear two-dimensional integral equations of the second kind on non-rectangular domains using radial basis functions with error analysis. J Comput Appl Math 239:72–92

    MathSciNet  MATH  Google Scholar 

  5. Assari P, Adibi H, Dehghan M (2014) A meshless discrete galerkin (MDG) method for the numerical solution of integral equations with logarithmic kernels. J Comput Appl Math 267:160–181

    MathSciNet  MATH  Google Scholar 

  6. Atkins DL, Ervin JS, Saxena A (2005) Computational model of the freezing of jet fuel. J Propul Power 21:356–367

    Google Scholar 

  7. Atluri SN, Zhu T (1998) A new meshless local Petrov–Galerkin (MLPG) approach in computational mechanics. Comput Mech 22:117–127

    MathSciNet  MATH  Google Scholar 

  8. Barry SI, Caunce J (2008) Exact and numerical solutions to a Stefan problem with two moving boundaries. Appl Math Model 32:83–98

    MATH  Google Scholar 

  9. Beck JV, Blackwell B, Clair CRS (1985) Inverse heat conduction, Ill-posed problems. Wiley, New York

    MATH  Google Scholar 

  10. Cannon JR (1967) The Cauchy problem for the heat equation. SIAM J Numer Anal 4:17–36

    MathSciNet  Google Scholar 

  11. Cannon JR (1984) The one-dimensional heat equation. Addison-Wesley, California

    MATH  Google Scholar 

  12. Cannon JR, Hill CD (1967) Existence, uniqueness, stability, and monotone dependence in a Stefan problem for the heat equation. SIAM J Numer Anal 17:1–19

    MathSciNet  MATH  Google Scholar 

  13. Cannon JR, Primicerio M (1971) Remarks on the one-phase Stefan problem for the heat equation with the flux prescribed on the fixed boundary. J Math Anal Appl 35:361–373

    MathSciNet  MATH  Google Scholar 

  14. Cannon JR, van der Hoek J (1982) The one phase Stefan problem subject to the specification of energy. J Math Anal Appl 86:281–291

    MathSciNet  MATH  Google Scholar 

  15. Chang CL (2002) Pretreatment of wastewater by vacuum freezing system in a cool thermal storage process. J Sep Purif Technol 26:165–176

    Google Scholar 

  16. Dehghan M, Abbaszadeh M (2016) Numerical study of three-dimensional turing patterns using a meshless method based on moving Kriging element free Galerkin (EFG) approach. Comput Math Appl 72:427–454

    MathSciNet  MATH  Google Scholar 

  17. Dehghan M, Abbaszadeh M (2017) Element free galerkin approach based on the reproducing kernel particle method for solving 2D fractional tricomi-type equation with Robin boundary condition. Comput Math Appl 73:1270–1285

    MathSciNet  MATH  Google Scholar 

  18. Dehghan M, Ghesmati A (2010) The meshless local Petrov–Galerkin (MLPG) method: a simple and less-costly alternative to the finite element and boundary element methods. Eng Anal Bound Elem 34:324–336

    MathSciNet  MATH  Google Scholar 

  19. Dehghan M, Mirzaei D (2008) The meshless local Petrov–Galerkin MLPG method for the generalized two-dimensional non-linear Schrodinger equation. Eng Anal Bound Elem 32:747–756

    MATH  Google Scholar 

  20. Dehghan M, Mirzaei D (2009) Meshless local boundary integral equation (LBIE) method for the unsteady magnetohydrodynamic (MHD) flow in rectangular and circular pipes. Comput Phys Commun 180:1458–1466

    MathSciNet  Google Scholar 

  21. Dehghan M, Mirzaei D (2009) Meshless local Petrov–Galerkin (MLPG) method for the unsteady magnetohydrodynamic (MHD) flow through pipe with arbitrary wall conductivity. Appl Numer Math 59:1043–1058

    MathSciNet  MATH  Google Scholar 

  22. Fasshauer G (2007) Meshfree approximation methods with MATLAB. Word Scientific Publishing, Singapore

    MATH  Google Scholar 

  23. Flannery BP, Press WH, Teukolsky SA, Vetterling WT (1996) Numerical recipes in Fortran 90: the art of parallel scientific computing. Cambridge University Press, New York

    MATH  Google Scholar 

  24. Griewank PJ, Notz D (2013) Insights into brine dynamics and sea ice desalination from a 1-d model study of gravity drainage. J Geophys Res Oceans 118:3370–3386

    Google Scholar 

  25. Grzymkowski R, Slota D (2006) One-phase inverse Stefan problem solved by Adomain decomposition method. Comput Math Appl 51:33–40

    MathSciNet  MATH  Google Scholar 

  26. Hemami M, Parand K, Rad JA (2019) Numerical simulation of reaction–diffusion neural dynamics models and their synchronization/desynchronization: application to epileptic seizures. Comput Math Appl (2019) (in press)

  27. Hetmaniok E, Slota D, Witula R, Zielonka A (2015) Solution of the one-phase inverse Stefan problem by using the homotopy analysis method. App Math Modell 39:6793–6805

    MathSciNet  MATH  Google Scholar 

  28. Crank J (1996) Free and moving boundary problems. Clarendon Press, Oxford

    MATH  Google Scholar 

  29. Jochum P (1980) The numerical solution of the inverse Stefan problem. Numer Math 34:411–429

    MathSciNet  MATH  Google Scholar 

  30. Johansson B, Lesnic D, Reeve T (2011) A method of fundamental solutions for the one-dimensional inverse Stefan problem. Appl Math Model 35:4367–4378

    MathSciNet  MATH  Google Scholar 

  31. Johansson BT, Lesnic D, Reeve T (2011) A method of fundamental solutions for the one-dimensional inverse Stefan problem. Appl Math Model 35:4367–4378

    MathSciNet  MATH  Google Scholar 

  32. Johansson BT, Lesnic D, Reeve T (2013) A meshless regularization method for a two-dimensional two-phase linear inverse Stefan problem. Adv Appl Math Mech 5(6):825–845

    MathSciNet  MATH  Google Scholar 

  33. Kazem S, Rad JA, Parand K (2012) Radial basis functions methods for solving Fokker–Planck equation. Eng Anal Bound Elem 36:181–189

    MathSciNet  MATH  Google Scholar 

  34. Lame G, Clapeyron BP (1831) Memoire sur la solidification par refroidissement d’un globe. Solide Ann Chem Phys 47:250–256

    Google Scholar 

  35. Larsson E, Shcherbakov V, Heryudono A (2017) A least squares radial basis function partition of unity method for solving PDEs. SIAM J Sci Comput 39:A2538–A2563

    MathSciNet  MATH  Google Scholar 

  36. Lin H, Atluri SN (2000) Meshless local Petrov–Galerkin (MLPG) method for convection–diffusion problems. Comput Model Eng Sci 1:45–60

    MathSciNet  Google Scholar 

  37. Liu CS (2011) Solving two typical inverse Stefan problems by using the Lie-group shooting method. Int J Heat Mass Transfer 54:1941–1949

    MATH  Google Scholar 

  38. Liu G (2009) Meshfree methods: moving beyond the finite element method. CRC Press, Boca Raton

    Google Scholar 

  39. Liu G, Gu Y (2005) An introduction to meshfree methods and their programing. Springer, Dordrecht

    Google Scholar 

  40. Loos F, Liess HT, Philippe B (2011) Transient analysis of the triggering behaviour of safety fuses. COMSOL Conference, Stuttgart, Germany

  41. Murio DA (1992) Solution of inverse heat conduction problems with phase changes by the mollification method. Comput Math Appl 24:45–57

    MathSciNet  MATH  Google Scholar 

  42. Needham DJ, Johansson B, Reeve T (2013) The development of a wax layer on the interior wall of a circular pipe transporting heated oil. Appl Math 67:93–125

    MathSciNet  MATH  Google Scholar 

  43. Notz D, Worster MG (2009) Desalination processes of sea ice revisited. J Geophys Res 14:1–10

    Google Scholar 

  44. Ostrov DN, Goodman J (2002) On the early exercise boundary of the American put option. SIAM J Appl Math 62:1823–1835

    MathSciNet  MATH  Google Scholar 

  45. Parand K, Rad JA (2012) Numerical solution of nonlinear Volterra–Fredholm–Hammerstein integral equations via collocation method based on radial basis functions. Appl Math Comput 218:5292–5309

    MathSciNet  MATH  Google Scholar 

  46. Parand K, Rad JA (2012) Kansa method for the solution of a parabolic equation with an unknown spacewise-dependent coefficient subject to an extra measurement. Comput Phys Commun 184(2013):582–595

    MathSciNet  Google Scholar 

  47. Quarteroni A, Sacco R, Saleri F (2000) Numerical mathematics. Springer, New York

    MATH  Google Scholar 

  48. Rad J, Parand K (2017) Pricing American options under jump-diffusion models using local weak form meshless techniques. I. J Comput Math 94:1694–1718

    MathSciNet  MATH  Google Scholar 

  49. Rad J, Rashedi K, Parand K, Adib H (2017) The meshfree strong form methods for solving one dimensional inverse Cauchy–Stefan problem. Eng Comput 33:547–571

    Google Scholar 

  50. Rad JA, Hook J, Larsson E, Sydow L (2018) Forward deterministic pricing of options using Gaussian radial basis functions. J Comput Sci 24:209–217

    MathSciNet  Google Scholar 

  51. Rad JA, Kazem S, Parand K (2012) A numerical solution of the nonlinear controlled Duffing oscillator by radial basis functions. Comput Math Appl 64:2049–2065

    MathSciNet  MATH  Google Scholar 

  52. Rad JA, Parand K (2017) Numerical pricing of American options under two stochastic factor models with jumps using a meshless local Petrov–Galerkin method. Appl Numer Math 115:252–274

    MathSciNet  MATH  Google Scholar 

  53. Rad JA, Parand K, Abbasbandy S (2015) Local weak form meshless techniques based on the radial point interpolation (RPI) method and local boundary integral equation (LBIE) method to evaluate European and American options. Commun Nonlinear Sci Numer Simul 22:1178–1200

    MathSciNet  MATH  Google Scholar 

  54. Rad JA, Parand K, Ballestra LV (2015) Pricing European and American options by radial basis point interpolation. Appl Math Comput 251:363–377

    MathSciNet  MATH  Google Scholar 

  55. Ramajayam KK, Kumar A (2013) A novel approach to improve the efficacy of tumour ablation during cryosurgery. Cryobiology 67:201–213

    Google Scholar 

  56. Rashedi K, Adibi H, Rad JA, Parand K (2014) Application of the meshfree methods for solving the inverse one-dimensional Stefan problem. Eng Anal Bound Elem 40:1–21

    MathSciNet  MATH  Google Scholar 

  57. Reemtsen R, Kirsch A (1984) A method for the numerical solution of the one-dimensional inverse Stefan problem. Numer Math 45:253–273

    MathSciNet  MATH  Google Scholar 

  58. Reeve TH (2013) The method of fundamental solutions for some direct and inverse problems. Ph. D. Dissertation, University of Birmingham

  59. Rippa S (1999) An algorithm for selecting a good parameter \(c\) in radial basis function interpolation. Adv Comput Math 11:193–210

    MathSciNet  MATH  Google Scholar 

  60. Rubinstein LI (1971) The Stefan problem. American Mathematical Society, Providence

    Google Scholar 

  61. Safdari-Vaighani A, Heryudono A, Larsson E (2015) A radial basis function partition of unity collocation method for convection–diffusion equations arising in financial applications. J Sci Comput 64:341–367

    MathSciNet  MATH  Google Scholar 

  62. Safdari-Vaighani A, Larsson E, Heryudono A (2018) Radial basis function methods for the Rosenau equation and other higher order PDEs. J Sci Comput 75:1555–1580

    MathSciNet  MATH  Google Scholar 

  63. Sarabadan S, Rashedi K, Adibi H (2017) Boundary determination of the inverse heat conduction problem in one and two dimensions via the collocation method based on the satisfier functions. Iran J Sci Technol Trans Sci. https://doi.org/10.1007/s40995-017-0240-y

    Article  MATH  Google Scholar 

  64. Seblani YE, Shivanian E (2019) Boundary value identification of inverse Cauchy problems in arbitrary plane domain through meshless radial point hermite interpolation. Eng Comput (2019) (in press)

  65. Shcherbakov V (2016) Radial basis function partition of unity operator splitting method for pricing multi-asset American options. BIT Numer Math 56:1401–1423

    MathSciNet  MATH  Google Scholar 

  66. Shcherbakov V, Larsson E (2016) Radial basis function partition of unity methods for pricing vanilla basket options. Comput Math Appl 71:185–200

    MathSciNet  MATH  Google Scholar 

  67. Shirzadi A, Ling L, Abbasbandy S (2012) Meshless simulations of the two-dimensional fractional-time convection–diffusion–reaction equations. Eng Anal Bound Elem 36:1522–1527

    MathSciNet  MATH  Google Scholar 

  68. Singh S, Bhargava R (2014) Simulation of phase transition during cryosurgical treatment of a tumor tissue loaded with nanoparticles using meshfree approach. J Heat Transf 136:121101–121110

    Google Scholar 

  69. Slota D (2007) Direct and inverse one-phase Stefan problem solved by variational iteration method. Comput Math Appl 54:1139–1146

    MathSciNet  MATH  Google Scholar 

  70. Slota D (2010) The application of the homotopy perturbation method to one-phase inverse Stefan problem. I. Commun Heat Mass Transf 37:587–592

    Google Scholar 

  71. Slota D, Zielonka A (2009) A new application of He’s variational iteration method for the solution of the one-phase Stefan problem. Comput Math Appl 58:2489–2494

    MathSciNet  MATH  Google Scholar 

  72. Smith GD (1985) Numerical solution of partial differential equations: finite difference methods. Oxford University Press, New York

    Google Scholar 

  73. Stefan J (1889) Uber einige probleme der theorie der warmeletung. S B Wien Akad Mat Nat 98:473–484

    Google Scholar 

  74. Vrankar L, Kansa EJ, Ling L, Runovc F, Turk G (2010) Moving-boundary problems solved by adaptive radial basis functions. Comput Fluids 39:1480–1490

    MathSciNet  MATH  Google Scholar 

  75. Vrankar L, Kansa EJ, Turk G, Runovc F (2006) Solving one-dimensional moving-boundary problems with meshless method. Math Ind 12:672–676

    MathSciNet  MATH  Google Scholar 

  76. Vrankar L, Runovc F, Turk G (2007) The use of the mesh free methods (radial basis functions) in the modeling of radionuclide migration and moving boundary value problems. Acta Geotech Sloven 1:43–53

    Google Scholar 

  77. Wang J, Liu G (2002) A point interpolation meshless method based on radial basis functions. Int J Numer Methods Eng 54:1623–1648

    MATH  Google Scholar 

  78. Wendland H (2005) Scattered data approximation. Cambridge University Press, New York

    MATH  Google Scholar 

  79. Zerroukat M, Chatwin CR (1994) Computational moving boundary problems. Research Studies Press, Taunton

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Sciences, Faculty of Mathematical Sciences, Shahid Beheshti University, G.C., Tehran, Iran

    Yasaman Lotfi & Kourosh Parand

  2. Department of Cognitive Modeling, Institute for Cognitive and Brain Sciences, Shahid Beheshti University, G.C., Tehran, Iran

    Kourosh Parand & Jamal Amani Rad

  3. Department of Mathematics, University of Science and Technology of Mazandaran, Behshahr, Iran

    Kamal Rashedi

Authors
  1. Yasaman Lotfi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kourosh Parand
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kamal Rashedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jamal Amani Rad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jamal Amani Rad.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lotfi, Y., Parand, K., Rashedi, K. et al. Numerical study of temperature distribution in an inverse moving boundary problem using a meshless method. Engineering with Computers 37, 461–475 (2021). https://doi.org/10.1007/s00366-019-00835-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00835-9

Keywords

Search

Navigation