Games with guaranteed scores and waiting moves | International Journal of Game Theory
Skip to main content
Springer Nature Link
Log in

Games with guaranteed scores and waiting moves

  • Original Paper
  • Published:
International Journal of Game Theory Aims and scope Submit manuscript

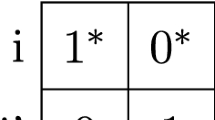
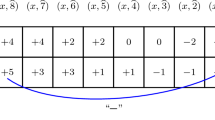
Abstract

Combinatorial scoring games, with the property ‘extra pass moves for a player will do him no harm’, are characterized. The characterization involves an order embedding of Conway’s normal play games, and we call our class the universe of Guaranteed scoring games. Also, we give a theorem for comparing guaranteed games with scores (numbers) which extends Ettinger’s work on Dicot scoring games.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. The first world championships, at TRUe games May 2014, were played on a \(8\times 8\) board with the middle \(2\times 2\) square empty. The authors placed 4th, 11th and 2nd respectively, Paul Ottaway placed 1st and Svenja Huntemann 3rd.

  2. see http://en.wikipedia.org/wiki/Game_of_the_Amazons.

References

  • Albert MH, Nowakowski RJ, Wolfe D (2007) Lessons in play. A K Peters Ltd, Natick

    Google Scholar 

  • Beck J (2006) Combinatorial games: tic-tac-toe theory. Series: encyclopedia of mathematics and its applications (No. 114). Cambridge University, Cambridge

    Google Scholar 

  • Berlekamp ER, Conway JH, Guy RK (2001) Winning ways for your mathematical plays, volume 1–4. A K Peters, Ltd., 2001–2004. 2nd edition: vols. 1

  • Calistrate D (1996) The reduced canonical form of a game, games of no chance, vol 29. MSRI Publications, Cambridge University, Cambridge

    Google Scholar 

  • Conway JH (1976) On numbers and games. Academic Press, London, p ix + 238

    Google Scholar 

  • Ettinger JM (2000) A metric for positional games. Theoret Comput Sci (Math Games) 230:207–219

    Article  Google Scholar 

  • Ettinger JM (1996) Topics in combinatorial games. PhD thesis, University of Wisconsin, Madison

  • Grossman JP, Siegel AN (2009) Reductions of partizan games. Games of no chance 3. Cambridge University, Cambridge, pp 437–456

    Google Scholar 

  • Hanner O (1959) Mean play of sums of positional games. Pac J Math 9:81–99

    Article  Google Scholar 

  • Johnson W (2014) The combinatorial game theory of well-tempered scoring games. Internat J Game Theory 43(2):415–438

    Article  Google Scholar 

  • Larsson U, Neto JP, Nowakowski RJ, Santos CP (2016) Guaranteed scoring games. Electron J Combin 23:3.27

    Google Scholar 

  • Milnor J (1953) Sums of positional games. Ann Math Stud 2(28):291–301 [(Contributions to the Theory of Games, Kuhn HW, Tucker AW (eds.)), Princeton]

    Google Scholar 

  • Plambeck TE, Siegel AN (2008) Misere quotients for impartial games. J Combin Theory Ser A 115(4):593–622

    Article  Google Scholar 

  • Santos CP, Carvalho A (2017) A non-trivial surjective map onto the short Conway’s Group. To appear. In: Larsson U (ed.) Games of no chance 5. In: Proceedings of BIRS workshop on combinatorial games, 2011, Banff, Alberta, Canada

  • Santos CP, Silva JN (2008) Konane has infinite Nim-dimension. INTEGERS 8(G2):6

    Google Scholar 

  • Siegel AN (2013) Combinatorial game theory. American Mathematical Society

  • Stewart F (2011) Scoring play combinatorial games. PhD thesis, University of Dundee, Also, to appear. In: Larsson U (ed.) Games of no chance 5. In: Proceedings of BIRS workshop on combinatorial games, 2011, Banff, Alberta, Canada

Download references

Author information

Authors and Affiliations

  1. Dalhousie University, Halifax, Canada

    Urban Larsson & Richard J. Nowakowski

  2. Center for Functional Analysis, Linear Structures and Applications, University of Lisbon, Lisbon, Portugal

    Carlos P. Santos

Authors
  1. Urban Larsson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Richard J. Nowakowski
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Carlos P. Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Carlos P. Santos.

Additional information

U. Larsson: Supported by the Killam Trust. C. P. Santos: This work was partially funded by Fundação para a Ciência e a Tecnologia through the project UID/MAT/04721/2013.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Larsson, U., Nowakowski, R.J. & Santos, C.P. Games with guaranteed scores and waiting moves. Int J Game Theory 47, 653–671 (2018). https://doi.org/10.1007/s00182-017-0590-x

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00182-017-0590-x

Keywords

Search

Navigation