Power Burr X-T family of distributions: properties, estimation methods and real-life applications | Computational Statistics Skip to main content
Springer Nature Link
Log in

Power Burr X-T family of distributions: properties, estimation methods and real-life applications

  • Original Paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

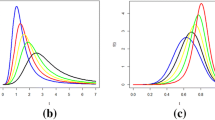
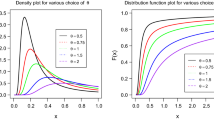
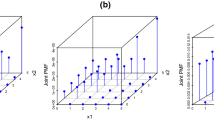
The new continuous class of probability distribution named the Power Burr X-T (PBX-T) family is proposed in this paper. The essential characteristics of the PBX-T family of distributions, i.e. conventional moments and associated procedures, stress-strength reliability, and Rényi entropy, are derived and studied. Some special models belonging to the new family have been comprehensively explored concerning their shapes. Extensive simulations have been conducted to compare the maximum likelihood (ML) estimates with other classical estimators. It is found that the mean squared errors and the bias of the ML estimates are relatively least for large samples. Moreover, real-life applications from medical and engineering fields have been used to demonstrate the potentiality and adequacy of the suggested sub-models from the PBX-T family. The values of observed goodness-of-fit measures show that the sub-models of the suggested family of distributions are superior in adequacy parallel to the other generalized models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability

All data used in this research is available and it will be provided on demand.

Code Availability

All the codes used in this research are available and will be provided upon request.

References

  • Afify AZ, Alizadeh M (2020) The odd Dagum family of distributions: properties and applications. J Appl Probab Stat 15:45–72

    Google Scholar 

  • Ahmad Sartawi H, Abu-Salih MS (1991) Bayesian prediction bounds for the Burr type X model. Commun Stat Theory Methods 20(7):2307–2330

    Article  MathSciNet  Google Scholar 

  • Aldahlan MA, Jamal F, Chesneau C, Elbatal I, Elgarhy M (2020) Exponentiated power generalized Weibull power series family of distributions: properties, estimation and applications. PLoS ONE 15(3):e0230004

    Article  Google Scholar 

  • Alizadeh M, Afify AZ, Eliwa M, Ali S (2020) The odd log-logistic Lindley-G family of distributions: properties, Bayesian and non-Bayesian estimation with applications. Comput Stat 35(1):281–308

    Article  MathSciNet  Google Scholar 

  • Almarashi AM, Elgarhy M, Jamal F, Chesneau C (2020) The exponentiated truncated inverse Weibull-generated family of distributions with applications. Symmetry 12(4):650

    Article  Google Scholar 

  • Alzaatreh A, Lee C, Famoye F (2013) A new method for generating families of continuous distributions. Metron 71(1):63–79

    Article  MathSciNet  Google Scholar 

  • Burr IW (1942) Cumulative frequency functions. Ann Math Stat 13(2):215–232

    Article  MathSciNet  Google Scholar 

  • Consul PC, Famoye F (2006) Lagrangian probability distributions. Springer, Berlin

    Google Scholar 

  • Cordeiro GM, Ortega EM, Popović BV, Pescim RR (2014) The Lomax generator of distributions: properties, minification process and regression model. Appl Math Comput 247(3):465–486

    MathSciNet  Google Scholar 

  • Cordeiro GM, Afify AZ, Yousof HM, Pescim RR, Aryal GR (2017) The exponentiated Weibull-H family of distributions: theory and applications. Mediterr J Math 14(4):155

    Article  MathSciNet  Google Scholar 

  • El-Bassiouny A, Abdo N, Shahen H (2015) Exponential lomax distribution. Int J Comput Appl 121(13):24–29

    Google Scholar 

  • El-Bassiouny A, El-Damcese M, Mustafa A, Eliwa M (2017) Exponentiated generalized Weibull–Gompertz distribution with application in survival analysis. J Stat Appl Probab 6(1):7–16

    Article  Google Scholar 

  • Elbatal I, Jamal F, Chesneau C, Elgarhy M, Alrajhi S (2019) The modified beta Gompertz distribution: theory and applications. Mathematics 7(1):3

    Article  Google Scholar 

  • Elgarhy M, Haq M, Ozel G (2017) A new exponentiated extended family of distributions with applications. Gazi Univ J Sci 30(3):101–115

    Google Scholar 

  • Eliwa M, El-Morshedy M (2020) Bivariate odd Weibull-G family of distributions: properties, Bayesian and non-Bayesian estimation with bootstrap confidence intervals and application. J Taibah Univ Sci 14(1):331–345

    Article  Google Scholar 

  • Eugene N, Lee C, Famoye F (2002) Beta-normal distribution and its applications. Communications in Statistics-Theory and Methods 31(4):497–512

    Article  MathSciNet  Google Scholar 

  • Handique L, ul Haq MA, Chakraborty S (2020) Generalized modified Exponential0G family of distributions: its properties and applications. Int J Math Stat 21(2020):1–17

    MathSciNet  Google Scholar 

  • Haq M, Elgarhy M (2018) The odd Fréchet-G family of probability distributions. J Stat Appl Probab 7(1):189–203

    Article  Google Scholar 

  • Jaheen Z (1996) Empirical Bayes estimation of the reliability and failure rate functions of the Burr type X failure model. J Appl Stat Sci 3(4):281–288

    MathSciNet  Google Scholar 

  • Jaheen ZF (1995) Bayesian approach to prediction with outliers from the Burr type X model. Microelectron Reliab 35(4):703–705

    Article  Google Scholar 

  • Jamal F, Nasir MA (2018) Generalized Burr X family of distributions. Int J Math Stat 19(2018):1–20

    MathSciNet  Google Scholar 

  • Johnson NL, Kotz S, Balakrishnan N (1994) Continuous univariate distributions. John Wiley, New York

    Google Scholar 

  • Kao JH (1958) Computer methods for estimating Weibull parameters in reliability studies. IRE Trans Reliab Qual Control. https://doi.org/10.1109/IRE-PGRQC.1958.500716415-22

    Article  Google Scholar 

  • Lee ET, Wang J (2003) Statistical methods for survival data analysis, vol 476. John Wiley & Sons, New York

    Book  Google Scholar 

  • Luceño A (2006) Fitting the generalized Pareto distribution to data using maximum goodness-of-fit estimators. Comput Stat Data Anal 51(2):904–917

    Article  MathSciNet  Google Scholar 

  • Mann NR, Schafer RE, Singpurwalla ND (1974) Methods for statistical analysis of reliability and life data(Book). Research supported by the U. S. Air Force and Rockwell International Corp. New York, John Wiley and Sons, Inc., 1974. p 573

  • Mudholkar GS, Srivastava DK (1993) Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans Reliab 42(2):299–302

    Article  Google Scholar 

  • Rényi A (1961) On measures of entropy and information. Paper presented at the Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics

  • Rodriguez RN (1977) A guide to the Burr type XII distributions. Biometrika 64(1):129–134

    Article  MathSciNet  Google Scholar 

  • Silva RCD, Sanchez JJ, Lima FP, Cordeiro GM (2021) The kumaraswamy gompertz distribution. J Data Sci 13(2):241–260

    Article  Google Scholar 

  • Surles J, Padgett W (2001) Inference for reliability and stress-strength for a scaled Burr Type X distribution. Lifetime Data Anal 7(2):187–200

    Article  MathSciNet  Google Scholar 

  • Surles J, Padgett W (2005) Some properties of a scaled Burr type X distribution. J Stat Plan Inference 128(1):271–280

    Article  MathSciNet  Google Scholar 

  • Usman RM, Ilyas M (2020) The power Burr type X distribution: properties, regression modeling and applications. Punjab Univ J Math 52(8):27–44

    MathSciNet  Google Scholar 

  • Wingo DR (1993) Maximum likelihood methods for fitting the Burr type XII distribution to multiply (progressively) censored life test data. Metrika 40(1):203–210

    Article  MathSciNet  Google Scholar 

  • Xu K, Xie M, Tang LC, Ho S (2003) Application of neural networks in forecasting engine systems reliability. Appl Soft Comput 2(4):255–268

    Article  Google Scholar 

  • Yousof HM, Afify AZ, Hamedani G, Aryal G (2017) The Burr X generator of distributions for lifetime data. J Stat Theory Appl 16(3):288–305

    Article  MathSciNet  Google Scholar 

Download references

Funding

The research receives no external funding.

Author information

Authors and Affiliations

  1. University of the Punjab, Lahore, Pakistan

    Rana Muhammad Usman & Maryam Ilyas

Authors
  1. Rana Muhammad Usman
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Maryam Ilyas
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All the authors significantly contribute in this research.

Corresponding author

Correspondence to Rana Muhammad Usman.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Usman, R.M., Ilyas, M. Power Burr X-T family of distributions: properties, estimation methods and real-life applications. Comput Stat 39, 2949–2974 (2024). https://doi.org/10.1007/s00180-023-01405-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-023-01405-w

Keywords