Examining the identifiability and estimability of the phase-type ageing model

Abstract

In this paper, the identifiability and the estimability of a particular phase-type ageing model (PTAM) are investigated. We consider a PTAM that is shown to be identifiable, although it has poor estimability when the only observation is the time until absorption. We use a data-cloning method to assess model estimability, which is also analysed visually via contour plots and marginal likelihood functions. The PTAM’s estimability under different scenarios is compared, from the best scenario of a fully observable Markov process for each individual to the worst scenario wherein the only observation is the time until absorption for each individual. Some in-between scenarios are also studied and include the situations where the state could be observed every several years and the state could be measured with some error. Certain conditions are provided regarding the state of the Markov chain that improves the PTAM’s estimability.

Appendices

Appendices

Appendix A: Flexibility of the PTAM’s resulting distribution

Obtaining a reasonably good fit for the PTAM was demonstrated in Sections 3.2 and 4.2 of Cheng et al. (2021). This motivated us to explore the flexibility of the PTAM. In particular, we consider the question: Can the PTAM achieve a good fit on any set of lifetime data? The assessment of the PTAM’s flexibility will be based on how well the resulting pdf and hazard function could approximate the true ones. Both functions are easily obtained from the data and commonly used to validate the calibrated result.

Definition A.1

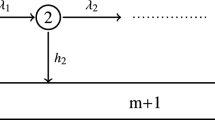
We define i as the state label for states $i=1,\ldots ,m$ in a Coxian model with m transient states.

Lemma A.1

Consider an $m-$state Coxian model with transition rate from one transient state to the next transient state equal to $\lambda$, and the absorption rate in state i is $h_i$ for $i=1,\ldots ,m$. For any $t>0$, let $Y_t$ be the state variable at time t. Then, $P(Y_t \ge k|Y_t \in E)$ is an increasing function with respect to t for any $k=1,\ldots ,m$.

Proof

The $m\times m$ intensity matrix of the Coxian model is

$$\begin{aligned} \varvec{\Lambda }=\left[ \begin{array}{ccccc} -\left( \lambda +h_{1}\right) &{} \lambda \\ &{} -\left( \lambda +h_{2}\right) &{} \lambda \\ &{} &{} \ddots \\ &{} &{} &{} -\left( \lambda +h_{m-1}\right) &{} \lambda \\ &{} &{} &{} &{} -h_{m} \end{array}\right] , \end{aligned}$$

where $\lambda$ is the rate of transition from state i to $i+1$, and $h_i$ is the absorption rate at state i. For any fixed $t>0$, let $Y_{\ell ,t}$ be the state random variable at time t assuming the starting state is $\ell$ at 0, then $Y_t=Y_{1,t}$. For every $k=1,{\ldots },m$,

$$\begin{aligned} P(Y_t \ge k|Y_{t} \in E)&=\frac{\sum _{j=k}^m P(Y_{1,t}=j)}{\sum _{j=1}^m P(Y_{1,t}=j)}=\frac{\varvec{\alpha }e^{\varvec{\Lambda }t} \varvec{e_{k}}}{\varvec{\alpha }e^{\varvec{\Lambda }t}\varvec{e}}, \end{aligned}$$

where $\varvec{e_{k}}$ is an $m\times 1$ column vector with first $k-1$ elements equal to 0 and the remaining elements are equal to 1. The quantity $P(Y_t \ge k|Y_t \in E)$ is the probability that the state of the individual at time t is greater than or equal to k conditional on this individual being alive. We note that $P(Y_t \ge 1|Y_{t} \in E)=1$. When $k \ne 1$, the first derivative of $P(Y_t \ge k|Y_t \in E)$ with respect to t is

$$\begin{aligned} \frac{\textrm{d}P(Y_t \ge k|Y_t \in E)}{\textrm{d}t}= \frac{\varvec{\alpha }e^{\varvec{\Lambda }t}(\varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha } -\varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda })e^{\varvec{\Lambda }t}\varvec{e}}{\left( \varvec{\alpha }e^{\varvec{\Lambda }t}\varvec{e}\right) ^2}. \end{aligned}$$

Let $g(t)=\varvec{\alpha }e^{\varvec{\Lambda }t}(\varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha } -\varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda })e^{\varvec{\Lambda }t}\varvec{e}$. The (i, j) entry of $e^{\varvec{\Lambda }t}$, denoted by $P_{i,j}(t)$, is the probability of being in state j at time t given that the starting state is i at time 0. It may be verified that

$$\begin{aligned} \varvec{\alpha }e^{\varvec{\Lambda }t}&=(P_{1,1}(t),...,P_{1,m}(t)) \, {\text {a }1\times m \text { row vector}}\\ e^{\varvec{\Lambda }t}\varvec{e}&=\left( \sum _{j=1}^mP_{1,j}(t),...,\sum _{j=1}^mP_{m,j}(t)\right) ^{\intercal }\, \text {an} m\times 1 \text { column vector}\\ \varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha }&=\left[ \begin{array}{ccccccc} 0 &{} 0&{}0&{}\cdots \\ \vdots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots \\ \lambda &{} 0&{}0&{}\cdots \\ -h_k &{} 0 &{}0 &{}\cdots \\ -h_{k+1} &{} 0 &{}0&{}\cdots \\ \vdots \\ -h_{m} &{} 0 &{}0&{}\cdots \end{array}\right] \, \text {an}\; m\times m \text { matrix}\\ \varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda }&=\left[ \begin{array}{ccccccc} 0 &{} 0&{}0&{}\cdots \\ \vdots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots \\ 0 &{} 0&{}0&{}\cdots \\ -(\lambda +h_1) &{} \lambda &{}0 &{}\cdots \\ -(\lambda +h_1) &{} \lambda &{}0&{}\cdots \\ \vdots \\ -(\lambda +h_1) &{} \lambda &{}0&{}\cdots \end{array}\right] \, \text {an} \;m\times m \text { matrix}, \end{aligned}$$

where $\lambda$ is the $(k-1,1)$ entry of $\varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha }$ and the entries of the entire first $(k-1)$th rows in $\varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda }$ are 0’s.

Remark A.1

Bold subscripts are used in the vector notation, and normal subscripts are associated to an element of a vector. For example, since $\varvec{A_k}$ is a vector, $\varvec{A}_k$ is the kth element of vector $\varvec{A}$.

Hence, $\varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha } -\varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda } =(\varvec{\beta _1},\varvec{\beta _2},\varvec{0},$...$,\varvec{0})^{\intercal }$, where $\varvec{\beta _2}$ is an $m\times 1$ column vector with the first $k-1$ elements all equal to 0 and the remaining elements are all equal to $-\lambda$; and $\varvec{\beta _1}$ is an $m\times 1$ column vector with the first $k-2$ elements equal to 0, the $(k-1)$th element equals $\lambda$, and the $\ell$th element ($\ell \ge k$) equals $\lambda +h_1-h_{\ell }$. In matrix form,

$$\begin{aligned} \varvec{\Lambda }\varvec{e_{k}}\varvec{\alpha } -\varvec{e_{k}}\varvec{\alpha }\varvec{\Lambda }=\left[ \begin{array}{ccccccc} 0 &{} 0&{}0&{}\cdots \\ \vdots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots \\ \lambda &{} 0&{}0&{}\cdots \\ \lambda +h_1-h_k &{} -\lambda &{}0 &{}\cdots \\ \lambda +h_1-h_{k+1} &{} -\lambda &{}0&{}\cdots \\ \vdots \\ \lambda +h_1-h_{m} &{} -\lambda &{}0&{}\cdots \end{array}\right] . \end{aligned}$$

Then, g(t) simplifies to

$$\begin{aligned} g(t)&=(P_{1,1}(t),{\ldots },P_{1,m}(t))\left[ \begin{array}{ccccccc} 0 &{} 0&{}0&{}\cdots \\ \vdots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots \\ \lambda &{} 0&{}0&{}\cdots \\ \lambda +h_1-h_k &{} -\lambda &{}0 &{}\cdots \\ \lambda +h_1-h_{k+1} &{} -\lambda &{}0&{}\cdots \\ \vdots \\ \lambda +h_1-h_{m} &{} -\lambda &{}0&{}\cdots \end{array}\right] \left( \sum _{j=1}^mP_{1,j}(t),...,\sum _{j=1}^mP_{m,j}(t)\right) ^{\intercal }\\&=\left( \left( \lambda P_{1,k-1}(t)+ \sum _{\ell =k}^m (\lambda +h_1-h_\ell ) P_{1,\ell }(t)\right) ,-\lambda \sum _{\ell =k}^m P_{1,\ell }(t),0,...,0\right) \left( \sum _{j=1}^mP_{1,j}(t),...,\sum _{j=1}^mP_{m,j}(t)\right) ^{\intercal } \\&=\left( \lambda P_{1,k-1}(t)+ \sum _{\ell =k}^m (\lambda +h_1-h_\ell ) P_{1,\ell }(t)\right) \sum _{j=1}^{m} P_{1,j}(t)-\sum _{\ell =k}^m \lambda P_{1,\ell }(t) \sum _{j=1}^m P_{2,j}(t). \end{aligned}$$

On the other hand, we know that

$$\begin{aligned} \frac{\textrm{d}e^{\varvec{\Lambda }t}}{\textrm{d}t} =\varvec{\Lambda }e^{\varvec{\Lambda }t}=e^{\varvec{\Lambda }t}\varvec{\Lambda }, \end{aligned}$$

yielding

$$\begin{aligned} \frac{\textrm{d}P_{1,k}(t)}{\textrm{d}t}&=-(\lambda +h_1)P_{1,k}(t)+\lambda P_{2,k}(t)=\lambda P_{1,k-1}(t)-(\lambda +h_k)P_{1,k}(t) \ \text {for} \ k=2,...,m-1\\ \frac{\textrm{d}P_{1,m}(t)}{\textrm{d}t}&=-(\lambda +h_1)P_{1,m}(t)+\lambda P_{2,m}(t)=\lambda P_{1,k-1}(t)-h_mP_{1,m}(t). \end{aligned}$$

Rearranging further, we have

$$\begin{aligned} (h_1-h_k)P_{1,k}(t)&=\lambda (P_{2,k}(t)-P_{1,k-1}(t)) \ \text {for} \ k=2,...,m-1\\ (\lambda +h_1-h_m)P_{1,m}(t)&=\lambda (P_{2,m}(t)-P_{1,m-1}(t)) \end{aligned}$$

The first part of g(t) could be written as

$$\begin{aligned}&\lambda P_{1,k-1}(t)+ \sum _{\ell =k}^m (\lambda +h_1-h_\ell ) P_{1,\ell }(t)\\&= \lambda P_{1,k-1}(t)+ \sum _{\ell =k}^{m-1} \lambda P_{1,\ell }(t)+\sum _{\ell =k}^{m-1} (h_1-h_\ell ) P_{1,\ell }(t)+(\lambda +h_1-h_m)P_{1,m}(t)\\&=\lambda P_{1,k-1}(t)+ \sum _{\ell =k}^{m-1} \lambda P_{1,\ell }(t)+\lambda \sum _{\ell =k}^m(P_{2,\ell }(t)-P_{1,\ell -1}(t)) =\lambda \sum _{\ell =k}^mP_{2,\ell }(t). \end{aligned}$$

Consequently,

$$\begin{aligned} g(t)=\lambda \left( \sum _{\ell =k}^mP_{2,\ell }(t)\sum _{j=1}^mP_{1,j}(t)-\sum _{\ell =k}^mP_{1,\ell }(t)\sum _{j=1}^mP_{2,j}(t)\right) , \end{aligned}$$

which shows that $g(t) \ge 0$ if and only if

$$\begin{aligned} P(Y_{1,t}\ge k|Y_{1,t} \in E)=\frac{\sum _{\ell =k}^mP_{1,\ell }(t)}{\sum _{j=1}^mP_{1,j}(t)} \le \frac{\sum _{\ell =k}^mP_{2,\ell }(t)}{\sum _{j=1}^mP_{2,j}(t)}=P(Y_{2,t}\ge k|Y_{2,t} \in E), \end{aligned}$$

with the equality holds if and only if $g(t)=0$. Similarly, $\frac{\textrm{d}P(Y_{\ell ,t}\ge k|Y_{\ell ,t} \in E)}{\textrm{d}t} \ge 0$ if and only if

$$\begin{aligned} P(Y_{\ell ,t}\ge k|Y_{\ell ,t} \in E) \le P(Y_{\ell +1,t}\ge k|Y_{\ell +1,t} \in E). \end{aligned}$$

(A.1)

The inequality is trivial when $\ell =m-1$ because $P(Y_{m,t}\ge k|Y_{m,t} \in E)=1$ and $P(Y_{\ell ,t}\ge k|Y_{\ell ,t} \in E) \le 1$. Recall that $Y_{\ell ,t}$ is the state variable at time t assuming the starting state is $\ell$ at time 0. By letting $t=0$, it could be verified that $P(Y_{\ell ,t=0}\ge k|Y_{\ell ,t=0} \in E)=1$ when $\ell \ge k$ and $P(Y_{\ell ,t=0}\ge k|Y_{\ell ,t=0} \in E)=0$ when $\ell < k$.

Since (A.1) holds when $\ell =m-1$, we have $\frac{\textrm{d}P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E)}{\textrm{d}t} \ge 0$, or $P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E)$ is increasing with respect to t.

The next step is to prove $P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E) \le P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E)$ by contradiction. Suppose

$$\begin{aligned} P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E) > P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E){.} \end{aligned}$$

(A.2)

By (A.1), we have $\frac{{\textrm{d}}P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E)}{{\textrm{d}}t}<0$, or $P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E)$ is decreasing with respect to t. Therefore, for any $t>0$,

$$\begin{aligned} P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E)&< P(Y_{m-2,t=0}\ge k|Y_{m-2,t=0} \in E)\\&\le P(Y_{m-1,t=0}\ge k|Y_{m-1,t=0} \in E)\\&< P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E), \end{aligned}$$

which conflicts with (A.2). The first inequality holds because $P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E)$ is decreasing with respect to t. The second inequality holds because $P(Y_{\ell ,t=0}\ge k|Y_{\ell ,t=0} \in E)$ is equal to 1 when $\ell \ge k$; otherwise, it is equal to 0, so that $P(Y_{m-1,t=0}\ge k|Y_{m-1,t=0} \in E)$ must be 1 if $P(Y_{m-2,t=0}\ge k|Y_{m-2,t=0} \in E)=1$ for any k. The third inequality holds because we proved $P(Y_{m-1,t}\ge k|Y_{m-1,t} \in E)$ is an increasing function of t.

Hence, (A.2) is false, and it must be that

$$\begin{aligned} P(Y_{m-2,t} \ge k|Y_{m-2,t} \in E) \le P(Y_{m-1,t} \ge k|Y_{m-1,t} \in E), \end{aligned}$$

which shows $P(Y_{m-2,t}\ge k|Y_{m-2,t} \in E)$ is increasing with respect to t by (A.1). Following the same procedure recursively, it could be shown that $P(Y_{1,t}\ge k|Y_{1,t} \in E) \le P(Y_{2,t}\ge k|Y_{2,t} \in E)$. Therefore, $g(t) \ge 0$ and $\frac{\textrm{d}P(Y_{t}\ge k|Y_{t} \in E)}{\textrm{d}t} \ge 0$, implying that $P(Y_{t}\ge k|Y_{t} \in E)$ is an increasing function of t. $\square$

Theorem A.1

Consider the Coxian model with 3 restrictions: (i) the process starts in state 1 at time 0; (ii) the transition of going out from each state must be either to the next transient state or to the absorbing state; and (iii) the rates of transition from one transient state to the next transient state are the same. Suppose the absorption rate of the Coxian model is monotone with respect to the state label. The resulting hazard rate h(t) of the Coxian model is increasing with respect to age t if and only if the absorption rate $h_i$ is increasing with respect to i.

Proof

For any $t \ge 0$, the resulting hazard rate is

$$\begin{aligned} h(t)=\frac{\varvec{\alpha }\exp (\varvec{\Lambda } t)}{\varvec{\alpha }\exp (\varvec{\Lambda } t)\varvec{e}} \varvec{h} = \sum _{i=1}^m h_i P(Y_t=i|Y_t \in E) ={{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_t}|Y_t \in E\right) {.} \end{aligned}$$

The above result shows that h(t) is the expected value of $(h_{Y_t}|Y_t \in E)$, where $Y_t$ takes a state value at time t and E is the set of all transient states $\{1,\ldots ,m\}$. The ith element of $\varvec{\alpha }\exp (\varvec{\Lambda } t)$ is the probability in state i at time t.

By Lemma A.1, for any $t_1<t_2$, $Y_{t_1}$ is less than $Y_{t_2}$ in stochastic order. It is well known that if the random variable A is less than the random variable B in stochastic order, then for any non-decreasing functions u, ${{\,\mathrm{\mathbb {E}}\,}}(u(A)) \le {{\,\mathrm{\mathbb {E}}\,}}(u(B))$. Hence, when $h_i$ is increasing with respect to i, for any $0 \le t_1<t_2$,

$$\begin{aligned} h(t_1)={{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_1}}\big |Y_{t_1} \in E\right) \le {{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_2}}\big |Y_{t_2} \in E\right) = h(t_2), \end{aligned}$$

implying that h(t) is increasing with respect to age t.

On the other hand, when h(t) is increasing with respect to t, for any $0 \le t_1<t_2$,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_1}}\big |Y_{t_1} \in E\right) =h(t_1)< h(t_2)={{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_2}}\big |Y_{t_2} \in E\right) . \end{aligned}$$

(A.3)

Suppose $h_i$ is decreasing with respect to i. Then, $-h_i$ is an increasing function. We showed that $Y_{t_1}$ is less than $Y_{t_2}$ in stochastic order. Therefore,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\left( -h_{Y_{t_1}}\big |Y_{t_1} \in E\right) \le {{\,\mathrm{\mathbb {E}}\,}}\left( -h_{Y_{t_2}}\big |Y_{t_2} \in E\right) , \end{aligned}$$

yielding ${{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_1}}\big |Y_{t_1} \in E\right) \ge {{\,\mathrm{\mathbb {E}}\,}}\left( h_{Y_{t_2}}\big |Y_{t_2} \in E\right)$. Or, $h(t_1)\ge h(t_2)$, which contradicts with h(t) being increasing. Consequently, the absorption rate $h_i$ is increasing with respect to i.

$\square$

Since the PTAM’s absorption rate is monotone, the resulting hazard rate is monotone by Theorem A.1. A non-monotonic hazard rate is an impossibility for the PTAM. Therefore, we only investigate the goodness of fit of certain lifetime distributions with monotonic hazard rate.

Remark A.2

Suppose the absorption rate of the Coxian model is monotone with respect to the state label. Then, the resulting hazard rate h(t) is decreasing with respect to age t if and only if the dying rate $h_i$ is decreasing with respect to i.

The following list includes the tested lifetime distributions we are interested in: (i) Gamma distribution with increasing hazard rate, (ii) Gamma distribution with decreasing hazard rate, (ii) Weibull distribution with increasing hazard rate, (iv) Weibull distribution with decreasing hazard rate, (v) Pareto distribution with decreasing hazard rate, (vi) Convolution of two exponential distributions, (vii) Convolution of two Weibull distributions, (viii) Gompertz-Makeham distribution, and (ix) Makeham’s second extension of the Gompertz distribution.

Our experiments demonstrate that the fitted results are promising for all tested distributions, except for the tail portion of heavy-tailed distributions. As expected, it is problematic to use light-tailed distributions, which include the PTAM, to approximate heavy-tailed distributions, because there is always a distinct tail requiring a large number of mixtures (states in the PTAM) to approximate well the tail. For example, Figures S.6 and S.8 of the Supplementary Material depict the typical fitted results for the heavy-tailed and light-tailed distributions, respectively. More discussion and fitted results are presented in Appendix B.

Appendix B: Experiments showing the flexibility of the resulting distribution from a PTAM

In this Appendix, we detail the analysis of PTAM’s flexibility as described in Appendix A. This is based on the concept of goodness-of-fit to the target distribution by the calibrated PTAM.

1.1 Appendix B.1: Some distributions for lifetime modelling

The Gamma distribution has two parameters: $\alpha$ and $\beta$. Its associated pdf is

$$\begin{aligned} f(t)=\frac{\beta ^{\alpha }}{\Gamma (\alpha )}t^{\alpha -1}\exp (-\beta t), \ \alpha>0, \ \beta >0, \end{aligned}$$

where $\Gamma (x)=\int _{z=0}^{\infty }z^{x-1}e^{-z}dz$ is the Gamma function. When $\alpha >1$, the Gamma distribution has an increasing hazard rate, whilst the hazard rate for a Gamma distribution is decreasing when $\alpha <1$. When $\alpha =1$, the Gamma distribution reduces to an exponential distribution with a rate $\lambda =\beta$. Since the family of Gamma distributions is rich and capable of reproducing a variety of distribution shapes, it is extensively used in lifetime modelling. The Gamma distribution is one of the potential lifetime distributions utilised to capture lifetime processes of humans and some other living things.

The Weibull distribution has two parameters: k and $\lambda .$ Its associated pdf is

$$\begin{aligned} f(t)=\frac{k}{\lambda }\left( \frac{t}{\lambda }\right) ^{k-1}\exp \left( -\left( \frac{t}{\lambda }\right) ^k\right) , \ \lambda>0, \ k>0. \end{aligned}$$

When $k>1$, the Weibull distribution has an increasing hazard rate, whilst the hazard rate is decreasing when $k<1$. A Weibull distribution where $k=1$ reduces to an exponential distribution with rate $\lambda$. The Weibull distribution is popular in survival analysis and affords a sound basis for modelling lifetime distributions.

The Pareto distribution has two parameters: k and $\sigma$. Its associated survival function is

$$\begin{aligned} S(t)=\left( 1+\frac{kt}{\sigma }\right) ^{-\frac{1}{k}}, \ k>0, \ \sigma >0. \end{aligned}$$

It is well-known that Pareto distributions are heavy-tailed.

A convolution of two exponential distributions has two parameters, and the random variable that represents a convolution of two exponential distributions is

$$\begin{aligned} Y=X_1+X_2, \end{aligned}$$

where $X_1$ and $X_2$ follow the exponential distributions with rates $\lambda _1$ and $\lambda _2$, respectively. The convolutions of different distributions have a physical interpretation; i.e, the process could be decomposed into several components and the time spent on each component follows a certain distribution. Specifically, the physical interpretation for the convolution mechanism is consistent with our cognizance of ageing, being a progressive process. Furthermore, it is often assumed that the time spent in each component follows an exponential distribution because an exponential distribution matches most observed data. Therefore, a convolution of exponential distributions is a further extension capable of accomplishing more flexibility.

A convolution of two Weibull distributions has four parameters, and the random variable representing a convolution of two Weibull distributions is

$$\begin{aligned} Z=W_1+W_2, \end{aligned}$$

where $W_1$ and $W_2$ follow the Weibull distribution with parameters $(\lambda _1, k_1)$ and $(\lambda _2, k_2)$ respectively. This is a simple extension of the previous example by changing the distributions of each component, similar to Huzurbazar (1999). Since the Weibull distribution is utilised in survival analysis, it is plausible for the ageing process that the time spent in each component follows a Weibull distribution as well. It is then worth exploring whether one could use the PTAM to approximate well a convolution of Weibull distributions.

The Gompertz-Makeham distribution has three parameters, and its associated hazard rate is

$$\begin{aligned} h(t)=\zeta +\xi \exp (\lambda t), \ \zeta \ge -\xi , \ \xi>0, \ \lambda >0{,} \end{aligned}$$

where $\xi$ is the growth rate of mortality and $\zeta$ represents the background mortality with additional constraint $\zeta > 0$.

The Gompertz-Makeham distribution were proposed by Makeham (1860) and Gompertz (1825), and it assumes a shifted exponential increasing hazard rate with respect to age. Such a distribution fits human mortality rates from age 30 to 80 well. When we calibrate the PTAM with human lifetime observations only, the PTAM is essentially approximating the Gompertz-Makeham distribution.

The Makeham’s second extension of the Gompertz distribution has four parameters, and its survival function is

$$\begin{aligned} S(t)=\exp \left( -\xi (\exp (\lambda t)-1)-\xi \theta \lambda t-\xi \alpha (\lambda t)^2\right) , \ \xi>0, \ \lambda>0, \ \theta>0, \ \alpha >0. \end{aligned}$$

Makeham (1889) extended the assumptions on the differential equation for the hazard rate to higher-order derivatives. This was motivated by the observation that the third-order derivatives of the empirical hazard rates were much closer to a geometric progression. One may verify that the third-order derivatives, with respect to time t, of the hazard rate arising from the Makeham’s second extension of the Gompertz distribution is $\xi \lambda ^3(\exp (\lambda ))^t$, which is a geometric progression with initial value $\xi \lambda ^3$ and common ratio $\exp (\lambda )$.

Once again, it is likely to observe human lifetimes following the extended Gompertz distribution. For each example, we select appropriate parameter values to achieve a particular shape of probability density function or hazard function. Once the parameter values are chosen, the target lifetime distributions are completely determined.

1.2 Appendix B.2: Calibration criterion

We shall use the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951; Kullback 1997) to summarise the information loss when using the PTAM to approximate the target lifetime distribution, which is known. When calibrating the PTAM, we minimise the KL divergence to ensure minimal lost information.

Definition B.1

For continuous distributions P and Q with respective pdf’s p(x) and q(x) defined on a sample probability space, the KL divergence $D_{KL}$ of Q from P is

$$\begin{aligned} D_{KL}(P\ || \ Q){:=}\int _{-\infty }^{+\infty }p(x)\log \left( \frac{p(x)}{q(x)}\right) \textrm{d}x{.} \end{aligned}$$

Usually, the distribution P represents the actual model, and the distribution Q represents the distribution used to approximate P. In our case, the distribution P is the target lifetime distribution in each example, and the distribution Q is the PTAM.

The KL divergence’s non-negativity is a nice property as discussed further below. Specifically,

$$\begin{aligned} D_{KL}(P\ || \ Q) \ge 0, \end{aligned}$$

with equality if and only if $P=Q$. This result is known as the Gibbs’ inequality (Gibbs 1902). Thus, the divergence value could be interpreted as the extra information required for Q to represent P. Therefore, the smaller the divergence, the less extra information is required when using Q to approximate P and the better goodness of fit is for Q. Furthermore, by its non-negative property, the closer the divergence value to 0, the better the approximation.

In our case, we calibrate the PTAM by minimising the KL divergence of the PTAM from the target lifetime distribution. The analytical formula for the PTAM’s resulting distribution is quite involved. However, the resulting distribution is fairly easy to evaluate numerically for a given set of parameter values. Therefore, we numerically search for the minimum of $D_{KL}(\text {lifetime distribution} \ || \ \text {proposed PTAM})$, where p(x) is the pdf of the target lifetime distribution, q(x) is the pdf of the PTAM, and

$$\begin{aligned} D_{KL}(\text {lifetime distribution} \ || \ \text {proposed PTAM})=\int _{0}^{+\infty }p(x)\log \left( \frac{p(x)}{q(x)}\right) \textrm{d}x. \end{aligned}$$

The numerical search utilises the optimisation function fmincon in MATLAB. The calibration process is similar to the model calibration in the Le Bras model simulation in Cheng et al. (2021), except for switching the optimisation criterion from negative log-likelihood to the KL divergence. The Tail Value-at-Risk (TVaR) with risk level 0.999 denoted by $\text {TVaR}_{0.999}(T)$ is calculated in each example, and the calculated value is used to estimate $\psi$. The estimated values for the other four parameters are the values that minimise the divergence. For the fitted results, refer to Tables S.1 – S.10 and Figures S.1 – S.10 of the Supplementary Material.