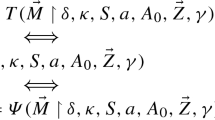Collapsing $$\omega _2$$ with semi-proper forcing | Archive for Mathematical Logic
Skip to main content
Springer Nature Link
Log in

Collapsing \(\omega _2\) with semi-proper forcing

  • Published:
Archive for Mathematical Logic Aims and scope Submit manuscript

Abstract

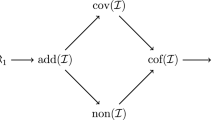
We examine the differences between three standard classes of forcing notions relative to the way they collapse the continuum. It turns out that proper and semi-proper posets behave differently in that respect from the class of posets that preserve stationary subsets of \(\omega _1\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baumgartner, J.E., Taylor, A.D.: Saturation properties of ideals in generic extensions. I. Trans. Am. Math. Soc. 270(2), 557–574 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  2. Beaudoin, R.E.: The proper forcing axiom and stationary set reflection. Pac. J. Math. 149(1), 13–24 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Foreman, M., Todorcevic, S.: A new Löwenheim–Skolem theorem. Trans. Am. Math. Soc. 357(5), 1693–1715 (2005)

    Article  MATH  Google Scholar 

  4. Gitik, M.: Nonsplitting subset of \({\cal{P}}_\kappa (\kappa ^{+})\). J. Symb. Logic. 50(4), 881–894 (1985)

    Article  MathSciNet  Google Scholar 

  5. Jech, T.: Set theory. Springer monographs in mathematics. Springer, Berlin (2003). (The third edition, revised and expanded)

    Google Scholar 

  6. Namba, K.: \((\omega _{1},\,2)\)-distributive law and perfect sets in generalized Baire space. Comment. Math. Univ. St. Paul. 20:107–126 (1971/1972)

  7. Rosłanowski, A., Shelah, S.: More forcing notions imply diamond. Arch. Math. Logic 35(5–6), 299–313 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  8. Shelah, S.: Semiproper forcing axiom implies Martin maximum but not \({\text{ PFA }}^+\). J. Symb. Logic 52(2), 360–367 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  9. Shelah, S.: Cardinal arithmetic, volume 29 of Oxford logic guides. Oxford University Press, New York (1994)

    Google Scholar 

  10. Todorcevic, S.: A note on the proper forcing axiom. In: Axiomatic set theory (Boulder, Colo., 1983), volume 31 of Contemporary mathematics, pp. 209–218. American Mathematics Society, Providence, RI (1984)

  11. Todorcevic, S.: Oscillations of real numbers. In: Logic colloquium ’86 (Hull, 1986), volume 124 of Studies in logic and the foundations of mathematics, pp. 325–331. North-Holland, Amsterdam (1988)

  12. Todorcevic, S.: Localized reflection and fragments of PFA. In: Set theory (Piscataway, NJ, 1999), volume 58 of DIMACS series in discrete mathematics and theoretical computer science, pp. 135–148. American Mathematics Society, Providence, RI (2002)

  13. Todorcevic, S.: Walks on ordinals and their characteristics, volume 263 of progress in mathematics. Birkhäuser Verlag, Basel (2007)

    Google Scholar 

  14. Todorcevic, Stevo.: Notes on forcing axioms, volume 26 of Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore. World Scientific Publishing Co., Pte. Ltd., Hackensack, NJ: Edited and with a foreword by Chong, C., Feng, Q., Yang, Y., Slaman, T.A., Woodin, W.H. (2014)

  15. Woodin, H.W.: The axiom of determinacy, forcing axioms, and the nonstationary ideal, volume 1 of de Gruyter series in logic and its applications. Walter de Gruyter & Co., Berlin (1999)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Toronto, Toronto, Canada

    Stevo Todorcevic

  2. Institut de Mathématiques de Jussieu, Paris, France

    Stevo Todorcevic

Authors
  1. Stevo Todorcevic
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stevo Todorcevic.

Additional information

Research partially supported by grants from NSERC and CNRS.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Todorcevic, S. Collapsing \(\omega _2\) with semi-proper forcing. Arch. Math. Logic 57, 185–194 (2018). https://doi.org/10.1007/s00153-017-0588-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00153-017-0588-x

Keywords

Mathematics Subject Classification

Search

Navigation