A Robust Resilient Multi-Objective Delay-Dependent Tracker for Nonlinear Time-Delay Systems | Circuits, Systems, and Signal Processing Skip to main content
Springer Nature Link
Log in

A Robust Resilient Multi-Objective Delay-Dependent Tracker for Nonlinear Time-Delay Systems

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

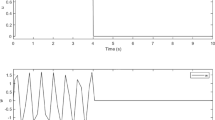
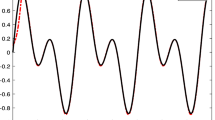
In this paper, a multi-objective robust tracking problem for nonlinear time-invariant systems with known time delay in state vector and control input is discussed. An augmented integral error is included in the tracking performance index which eliminates the effect of deterministic constant disturbances in the tracking problem. Uncertainties are considered as a nonlinear additive term in the problem. The discretized complete Lyapunov–Krasovskii functional (LKF) is used to formulate the robust resilient tracker with general quadratic performance. This approach yields much less conservatism than the conventional simple LKF design methods, and still allows writing both LKF and LKF derivative conditions in the form of linear matrix inequalities. Two comparative examples are given to illustrate the effectiveness of the proposed design method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. P.-A. Bliman, Lyapunov equation for the stability of linear delay systems of retarded and neutral type. IEEE Trans. Autom. Control 47, 327–335 (2002)

    Article  MathSciNet  Google Scholar 

  2. E.K. Boukas, M.S. Mahmoud, A practical approach to control of nonlinear discrete-time state-delay systems. Optim. Control Appl. Methods 28(5), 397–417 (2007)

    Article  MathSciNet  Google Scholar 

  3. S. Boyd, L.E. Ghaoui, E. Feron, V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory (SIAM, Philadelphia, 1994)

    Book  MATH  Google Scholar 

  4. Y.Y. Cao, Y.X. Sun, J. Lam, Delay-dependent robust H ∞ control for uncertain systems with time-varying delays. IEE Proc., Control Theory Appl. 145, 338–344 (1998)

    Article  Google Scholar 

  5. J. Cao, S. Zhong, Y. Hu, Delay-dependent condition for absolute stability of Lurie control systems with multiple time delays and nonlinearities. J. Math. Anal. Appl. 338, 497–504 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. E. Fridman, Descriptor discretized Lyapunov functional method: analysis and design. IEEE Trans. Autom. Control 51, 890–897 (2006)

    Article  MathSciNet  Google Scholar 

  7. E. Fridman, U. Shaked, New bounded real lemma representations for time-delay systems and their applications. IEEE Trans. Autom. Control 46, 1973–1979 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  8. E. Fridman, U. Shaked, A descriptor system approach to H ∞ control of linear time-delay systems. IEEE Trans. Autom. Control 47, 253–270 (2002)

    Article  MathSciNet  Google Scholar 

  9. E. Fridman, U. Shaked, Stability and H ∞ control of systems with time-varying delays, in Proceedings of IFAC Triennial World Congress, Barcelona, Spain (2002)

    Google Scholar 

  10. E. Fridman, U. Shaked, Parameter dependent stability and stabilization of uncertain time-delay systems. IEEE Trans. Autom. Control 48, 861–866 (2003)

    Article  MathSciNet  Google Scholar 

  11. K. Gu, Discretized LMI set in the stability problem of linear time-delay systems. Int. J. Control 68, 923–934 (1997)

    Article  MATH  Google Scholar 

  12. K. Gu, A further refinement of discretized Lyapunov functional method for the time-delay systems. Int. J. Control 74, 967–976 (2001)

    Article  MATH  Google Scholar 

  13. K. Gu, V. Kharitonov, J. Chen, Stability of Time-Delay Systems (Birkhäuser, Boston, 2003)

    Book  MATH  Google Scholar 

  14. Q.L. Han, On stability of linear neutral systems with mixed time delays: a discretised Lyapunov functional approach. Automatica 41, 1209–1218 (2005)

    Article  MATH  Google Scholar 

  15. Q.-L. Han, A delay decomposition approach to stability and H ∞ control of linear time-delay systems—Part II: H ∞ control, in Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China (2008), pp. 25–27

    Google Scholar 

  16. Q.-L. Han, A discrete delay decomposition approach to stability of linear retarded and neutral systems. Automatica 45(2), 517–524 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Q.L. Han, X. Yu, K. Gu, On computing the maximum time-delay bound for stability of linear neutral systems. IEEE Trans. Autom. Control 49, 2281–2285 (2004)

    Article  MathSciNet  Google Scholar 

  18. Y. He, G.P. Liu, D. Rees, M. Wu, Improved H ∞ filtering for systems with a time-varying delay. Circuits Syst. Signal Process. 29, 377–389 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. J.-L. Hong, An H ∞ output feedback control for discrete-time state-delayed systems. Circuits Syst. Signal Process. 23(4), 255–272 (2004)

    Article  MATH  Google Scholar 

  20. C.H. Lien, K.W. Yu, Robust reliable control for uncertain time-delay systems with IQC performance. Optim. Theory Appl. 138, 235–251 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. M.S. Mahmoud, Resilient Control of Uncertain Dynamical Systems (Springer, Heidelberg, 2004)

    Book  MATH  Google Scholar 

  22. M.S. Mahmoud, Switched Time-Delay Systems (Springer, Boston, 2010)

    Book  MATH  Google Scholar 

  23. M.S. Mahmoud, N.B. Almutairi, Resilient decentralized stabilization of interconnected time-delays systems with polytopic uncertainties. Int. J. Robust Nonlinear Control 21(4), 355–372 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. M.S. Mahmoud, A. Ismail, Resilient control of nonlinear discrete-time state-delay systems. Appl. Math. Comput. 206(2), 561–569 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  25. M.S. Mahmoud, E.K. Boukas, P. Shi, Resilient feedback stabilization of discrete-time systems with delays. IMA J. Math. Control Inf. 25(2), 141–156 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  26. P.T. Nam, V.N. Phat, Robust stabilization of linear systems with delayed state and control. Optim. Theory Appl. 140, 287–299 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. R.M. Palhares, C.D. Campos, P.Ya. Ekel, M.C.R. Leles, M.F.S.V. D’Angelo, Delay-dependent robust H ∞ control of uncertain linear systems with lumped delays. IEE Proc., Control Theory Appl. 152, 27–33 (2005)

    Article  Google Scholar 

  28. R.M. Palhares, C.D. Campos, P.Ya. Ekel, M.C.R. Leles, M.F.S.V. D’Angelo, Delay-dependent robust H ∞ control of uncertain linear systems with time-varying delays. Comput. Math. Appl. 50, 13–32 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. D. Peng, X. Guan, Output feedback H ∞ control for 2-D state-delayed systems. Circuits Syst. Signal Process. 28, 147–167 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. J.P. Richard, Time-delay systems: an overview of some recent advances and open problems. Automatica 39, 1667–1694 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  31. C. Scherer, P. Gahinet, M. Chilali, Multiobjective output-feedback control via LMI optimization. IEEE Trans. Autom. Control 42, 896–911 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  32. D.D. Siljak, D. Stipanovic, Robust stabilization of nonlinear systems. Math. Probl. Eng. 6, 461–493 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  33. F.O. Souza, R.M. Palhares, K.A. Barbosa, New improved delay-dependent H ∞ filter design for uncertain neutral systems. IET Control Theory Appl. 2(12), 1033–1043 (2008)

    Article  MathSciNet  Google Scholar 

  34. F.O. Souza, R.M. Palhares, V.J.S. Leite, Improved robust H ∞ control for neutral systems via discretised Lyapunov–Krasovskii functional. Int. J. Control 81, 1462–1474 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. X. Wan, H. Fang, S. Fu, Observer-based fault detection for networked discrete-time infinite-distributed delay systems with packet dropouts. Appl. Math. Model. 36(1), 270–278 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  36. L. Xie, E. Fridman, U. Shaked, Robust control of distributed delay systems with application to combustion control. IEEE Trans. Autom. Control 46, 1930–1935 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  37. S. Xu, G. Feng, Improved robust absolute stability criteria for uncertain time-delay systems. IET Control Theory Appl. 1(6), 1630–1637 (2007)

    Article  Google Scholar 

  38. S. Xu, J. Lam, A survey of linear matrix inequality techniques in stability analysis of delay systems. Int. J. Syst. Sci. 39, 1095–1113 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Intelligent Control Systems Laboratory, School of Electrical and Computer Engineering, Tarbiat Modares University, P.O. Box 14115-194, Tehran, Iran

    Mahdi Sojoodi & Vahid Johari Majd

Authors
  1. Mahdi Sojoodi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Vahid Johari Majd
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vahid Johari Majd.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sojoodi, M., Majd, V.J. A Robust Resilient Multi-Objective Delay-Dependent Tracker for Nonlinear Time-Delay Systems. Circuits Syst Signal Process 31, 1951–1971 (2012). https://doi.org/10.1007/s00034-012-9419-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-012-9419-9

Keywords