Graham's problem on shortest networks for points on a circle | Algorithmica Skip to main content
Springer Nature Link
Log in

Graham's problem on shortest networks for points on a circle

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

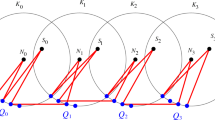
Suppose a configurationX consists ofn points lying on a circle of radiusr. If at most one of the edges joining neighboring points has length strictly greater thanr, then the Steiner treeS consists of all these edges with a longest edge removed. In order to showS is, in fact, just the minimal spanning treeT, a variational approach is used to show the Steiner ratio for this configuration is at least one and equals one only ifS andT coincide. The variational approach greatly reduces the number of possible Steiner trees that need to be considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. Z. Du, F. K. Hwang, and S. C. Chao, Steiner Minimal Tree for Points on a Circle,Proc. Amer. Math. Soc.,95 (1985), 613–618.

    Article  MATH  MathSciNet  Google Scholar 

  2. M. R. Garey, R. L. Graham, and D. S. Johnson, The Complexity of Computing Steiner Minimal Trees,SIAM J. Appl. Math.,32 (1977), 835–859.

    Article  MATH  MathSciNet  Google Scholar 

  3. E. N. Gilbert and H. O. Pollak, Steiner Minimal Trees,SIAM J. Appl. Math.,16 (1968), 1–29.

    Article  MATH  MathSciNet  Google Scholar 

  4. R. L. Graham, Some Results on Steiner Minimal Trees, Unpublished manuscript dated 11 May 1967.

  5. Z. A. Melzak, On the Problem of Steiner,Canad. Math. Bull,4 (1961), 143–148.

    MATH  MathSciNet  Google Scholar 

  6. H. O. Pollak, Some Remarks on the Steiner Problem,J. Combin. Theory Ser. A,24 (1978), 278–295.

    Article  MATH  MathSciNet  Google Scholar 

  7. J. H. Rubinstein and D. A. Thomas, A Variational Approach to the Steiner Network Problem, Preprint.

  8. J. H. Rubinstein and D. A. Thomas, Critical Points for the Steiner Ratio Conjecture, Preprint.

  9. J. H. Rubinstein and D. A. Thomas, The Steiner Ratio Conjecture for Cocircular Points, Preprint.

  10. J. H. Rubinstein and D. A. Thomas, The Steiner Ratio Conjecture for Six Points, Preprint.

  11. J. H. Rubinstein, D. A. Thomas, and J. F. Weng, Degree Five Steiner Points Cannot Reduce Network Costs for Planar Sets, Preprint.

Download references

Author information

Authors and Affiliations

  1. Institute of Advanced Study, and Mathematics Department, University of Melbourne, 3052, Parkville, Victoria, Australia

    J. H. Rubinstein

  2. University of Melbourne, 3052, Parkville, Victoria, Australia

    D. A. Thomas

Authors
  1. J. H. Rubinstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. A. Thomas
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by F. K. Hwang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rubinstein, J.H., Thomas, D.A. Graham's problem on shortest networks for points on a circle. Algorithmica 7, 193–218 (1992). https://doi.org/10.1007/BF01758758

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01758758

Key words

Search

Navigation