Neural Network Algorithm for Solving Nonlinear Equation Systems

Abstract

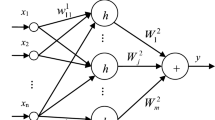
In practical research, nonlinear equation systems (NESs) are common mathematical models widely applied across various fields. Solving these nonlinear equation systems is crucial for addressing many engineering challenges. However, due to the inherent complexity and diverse solutions of nonlinear equation systems, traditional optimization algorithms and intelligent optimization algorithms have certain limitations. Neural network algorithms, which have gained significant popularity in recent years, excel in fitting nonlinear relationships. This research aims to explore different neural network models to develop efficient and accurate computational models for solving various types of nonlinear equation systems, thus overcoming some of the limitations of traditional and intelligent optimization algorithms. By leveraging the adaptability and generality of neural networks, we seek to enhance their performance in solving complex nonlinear equation systems. Furthermore, by integrating iterative algorithms and clustering algorithms, we aim to improve solution accuracy and effectively address the multiple roots problem associated with nonlinear equation systems.