Abstract
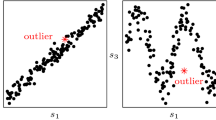
The data structure is becoming more and more complex, and the scale of the data set is getting larger and larger. The strong limitations and instability in the high-dimensional data environment is showed in traditional outlier detection method. To solve the problems, an Optimal subspace Analysis based on Information-entropy Increment is proposed. The concepts such as mutual information and dimensional entropy to re-portrait the indicators that measure the pros and cons of subspace clustering, optimize the objective function of the clustering subspace, and obtain the optimal subspace. According to the idea of dividing the information entropy increment by one, the entropy outlier score is proposed as a metric to detect outliers in the optimal subspace. Finally, experiments verify the effectiveness of the algorithm.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Gautam, B., Koushik, G., et al.: Outlier detection using neighborhood rank difference. Pattern Recogn. Lett. 60, 24–31 (2015)
Breunig, M.M., Kriegel, H.P., Ng, R.T., et al.: LOF: identifying density-based local outliers. In: Hen, W.D.C., Naught, J.F., Bernstein, P.A. (eds.) Proceedings of the 2000 ACMSIGMOD International Conference on Management of Data, pp. 93–104. ACM, New York (2000)
Kontaki, M., Gounaris, A., Papadopoulos, A.N., et al.: Efficient and flexible algorithms for monitoring distance-based outliers over data streams. Inf. Syst. 55, 37–53 (2016)
Clamond, D., Dutykh, D.: Accurate fast computation of steady two-dimensional surface gravity waves in arbitrary depth. J. Fluid Mech. 844, 491–518 (2018)
Wu, S., Wang, S.R.: Information-theoretic outlier detection for large-scale categorical data. IEEE Trans. Knowl. Data Eng. 25(3), 589–602 (2013)
Chi, Z., Dong, L., Wei, F., et al.: InfoXLM: an information-theoretic framework for cross-lingual language model pre-training. 32, 154–159 (2020)
Coccarelli, D., Greenberg, J.A., Mandava, S., et al.: Creating an experimental testbed for information-theoretic analysis of architectures for x-ray anomaly detection. In: SPIE Defense + Security, pp. 69–72 (2017)
Zhang, Z., Qiu, J., Liu, C., et al.: Outlier detection algorithm based on clustering outlier factor and mutual density. Comput. Integr. Manuf. Syst. 2019(9), 2314–2323
Zhang, Z., Fang, C.: Subspace clustering outlier detection algorithm based on cumulative total entropy. Comput. Integr. Manuf. Syst. 21(8), 2249–2256 (2015)
Li, J., Zhang, C., Fan, H.: Swarm intelligent point cloud smoothing and denoising algorithm. Comput. Integr. Manuf. Syst. 17(5), 935–945 (2011)
Department of Inorganic Chemistry, Beijing Normal University, Central China Normal University, Nanjing Normal University. Inorganic Chemistry, pp. 222–227. Higher Education Press, Beijing (2002)
Shannon, C.E.: A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 5(1), 3–55 (2001)
Liao, L., Luo, B.: Outlier detection algorithm based on dimensional entropy. Comput. Eng. Des. 40(4), 983–988 (2019)
Zhang, J., Sun, Z., Yang, M.: Mass data incremental outlier mining algorithm based on grid and density. Comput. Res. Dev. 48(5), 823–830 (2011)
Feng, J., Sun, Y.F., Cao, C.: An Information Entropy-Based Approach to Outlier Detection in Rough Sets. Pergamon Press Inc, Oxford (2010)
Li, J., Xun, Y.: Strong correlation subspace outlier detection algorithm. Comput. Eng. Des. 38(10), 2754–2758 (2017)
Duan, L., Xiong, D., Lee, J., et al.: A local density based spatial clustering algorithm with noise. In: IEEE International Conference on Systems, pp. 599–603. IEEE (2007)
Ning, J., Chen, L., Luo, Z., Zhou, C., Zeng, H.: The evaluation index of outlier detection algorithm. Comput. Appl. 27(11), 1–8 (2020)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Zhang, Z., Liu, I., Zhang, Y., Zhang, J., Tian, M. (2021). Optimal Subspace Analysis Based on Information-Entropy Increment. In: Mei, H., et al. Big Data. BigData 2020. Communications in Computer and Information Science, vol 1320. Springer, Singapore. https://doi.org/10.1007/978-981-16-0705-9_8
Download citation
DOI: https://doi.org/10.1007/978-981-16-0705-9_8
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-16-0704-2
Online ISBN: 978-981-16-0705-9
eBook Packages: Computer ScienceComputer Science (R0)