Abstract
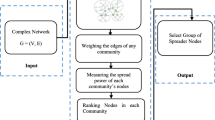
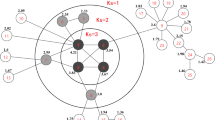
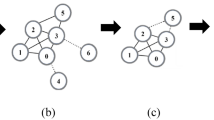
This paper addresses the issue of distinguishing influential nodes in the complex network. The k-shell index features embeddedness of a node in the network based upon its number of links with other nodes. This index filters out the most influential nodes with higher values for this index, however, fails to discriminate their scores with good resolution, hence results in assigning same scores to the nodes belonging to same k-shell set. Extending this index with neighborhood coreness of a node and also featuring topological connections between its neighbors, our proposed method can express the nodes influence score precisely and can offer distributed and monotonic rank orders than other node ordering methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Tan, Y.J., Wu, J. and Deng, H.Z.: Evaluation method for node importance based on node contraction in complex networks. Systems Engineering-Theory & Practice, 11(11), pp. 79–83(2006).
Wang, L. and Zhang, J.J.: Centralization of complex networks. Complex systems and complexity science, 3(1), pp. 13–20 (2006).
He, N., Li, D.Y., Gan, W. and Zhu, X.: Mining vital nodes in complex networks. Computer Science, 34(12), pp. 1–5 (2007).
Sun, R. and Luo, W.B.: Review on evaluation of node importance in public opinion. Jisuanji Yingyong Yanjiu, 29(10), pp. 3606–3608 (2012).
Kitsak, M., Gallos, L.K., Havlin, S., Liljeros, F., Muchnik, L., Stanley, H.E. and Makse, H.A.: Identification of influential spreaders in complex networks. Nature physics, 6(11), pp. 888–893 (2010).
Jiang, X., Sun, X. and Zhuge, H.: Graph-based algorithms for ranking researchers: not all swans are white!. Scientometrics, 96(3), pp. 743–759 (2013).
Lü, L., Zhang, Y.C., Yeung, C.H. and Zhou, T.: Leaders in social networks, the delicious case. PloS one, 6(6), p.e21202 (2011).
Albert, R., Jeong, H. and Barabási, A.L.: Error and attack tolerance of complex networks. Nature, 406(6794), pp. 378–382 (2000).
Feng, X., Sharma, A., Srivastava, J., Wu, S. and Tang, Z.: Social network regularized Sparse Linear Model for Top-N recommendation. Engineering Applications of Artificial Intelligence, 51, pp. 5–15 (2016).
Ma, L.L., Ma, C. and Zhang, H.F.: Identifying influential spreaders in complex networks based on gravity formula. arXiv preprint arXiv:1505.02476 (2015).
Page, L., Brin, S., Motwani, R. and Winograd, T.: The PageRank Citation Ranking: Bringing Order to the Web (1999). In Stanford InfoLab.
Kleinberg, J.M.: Authoritative sources in a hyperlinked environment. Journal of the ACM (JACM), 46(5), pp. 604–632 (1999).
Chen, D., Lü, L., Shang, M.S., Zhang, Y.C. and Zhou, T.: Identifying influential nodes in complex networks. Physica a: Statistical mechanics and its applications, 391(4), pp. 1777–1787 (2012).
Zeng, A. and Zhang, C.J.: Ranking spreaders by decomposing complex networks. Physics Letters A, 377(14), pp. 1031–1035 (2013).
Liu, J.G., Ren, Z.M. and Guo, Q.: Ranking the spreading influence in complex networks. Physica A: Statistical Mechanics and its Applications, 392(18), pp. 4154–4159 (2013).
Bae, J. and Kim, S.: Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Physica A: Statistical Mechanics and its Applications, 395, pp. 549–559 (2014).
Gao, S., Ma, J., Chen, Z., Wang, G. and Xing, C.: Ranking the spreading ability of nodes in complex networks based on local structure. Physica A: Statistical Mechanics and its Applications, 403, pp. 130–147 (2014).
Lawyer, G.: Understanding the influence of all nodes in a network. Scientific Reports, (2015) 5.
Narayanam, R. and Narahari, Y.: A shapley value-based approach to discover influential nodes in social networks. Automation Science and Engineering, IEEE Transactions on, 8(1), pp. 130–147 (2011).
Keeling, M.J. and Eames, K.T.: Networks and epidemic models. Journal of the Royal Society Interface, 2(4), pp. 295–307 (2005).
Albert, R. and Barabási, A.L.: Statistical mechanics of complex networks. Reviews of modern physics, 74(1), (2002), p. 47.
Sabidussi, G.: The centrality index of a graph. Psychometrika, 31(4), pp. 581–603 (1966).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Saxena, C., Doja, M.N., Ahmad, T. (2017). Neighborhood Topology to Discover Influential Nodes in a Complex Network. In: Satapathy, S., Bhateja, V., Udgata, S., Pattnaik, P. (eds) Proceedings of the 5th International Conference on Frontiers in Intelligent Computing: Theory and Applications . Advances in Intelligent Systems and Computing, vol 515. Springer, Singapore. https://doi.org/10.1007/978-981-10-3153-3_32
Download citation
DOI: https://doi.org/10.1007/978-981-10-3153-3_32
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-3152-6
Online ISBN: 978-981-10-3153-3
eBook Packages: EngineeringEngineering (R0)