Orders of Criticality in Graph Connection Games | SpringerLink
Skip to main content
Springer Nature Link
Log in

Orders of Criticality in Graph Connection Games

  • Chapter
  • First Online:
Transactions on Computational Collective Intelligence XXXIV

Part of the book series: Lecture Notes in Computer Science ((TCCI,volume 11890))

Abstract

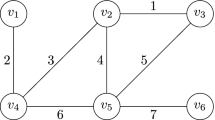
The order of criticality of a player in a simple game and two indices inspired by the reasoning à la Shapley and à la Banzhaf were introduced in two previous papers [3] and [4], respectively, mainly having in mind voting situations. Here, we devote our attention to graph connection games, and to the computation of the order of criticality of a player. The indices introduced in [4] may be used as centrality measures of the edges in preserving the connection of a graph.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 5719
Price includes VAT (Japan)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 7149
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    This property is called monotonicity.

  2. 2.

    In other terms, \(v(M \setminus T )=0\) or \(v(M \setminus (T \cup \{i\} ))=1\) for any \(T \subset M \setminus \{i\}\) with \(|T|< k\).

References

  1. Aziz, H., Lachish, O., Paterson, M., Savani, R.: Power indices in spanning connectivity games. In: Goldberg, A.V., Zhou, Y. (eds.) AAIM 2009. LNCS, vol. 5564, pp. 55–67. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02158-9_7

    Chapter  MATH  Google Scholar 

  2. Banzhaf, J.F.: Weighted voting doesn’t work: a mathematical analysis. Rutgers Law Rev. 19, 317–343 (1965)

    Google Scholar 

  3. Dall’Aglio, M., Fragnelli, V., Moretti, S.: Orders of criticality in voting games. Oper. Res. Decis. 26, 53–67 (2016)

    MathSciNet  MATH  Google Scholar 

  4. Dall’Aglio, M., Fragnelli, V., Moretti, S.: Indices of criticality in simple games. Int. Game Theory Rev. 21(01), 1–21 (2019)

    Article  MathSciNet  Google Scholar 

  5. Ford, L.R., Fulkerson, D.R.: Flows in Networks. Princeton University Press, Princeton (1962)

    MATH  Google Scholar 

  6. Holtkamp, A.: Maximal local edge-connectivity of diamond-free graphs. Australas. J. Comb. 49, 153–158 (2011)

    MathSciNet  MATH  Google Scholar 

  7. Menger, K.: Zur allgemeinen Kurventheorie. Fund. Math. 10, 96–115 (1927)

    Article  Google Scholar 

  8. Shapley, L.S., Shubik, M.: A method for evaluating the distribution of power in a committee system. Am. Polit. Sci. Rev. 48, 787–792 (1954)

    Article  Google Scholar 

  9. Volkmann, L.: On local connectivity of graphs. Appl. Math. Lett. 21, 63–66 (2008)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the participants to the workshop “Quantitative methods of group decision making” held at the Wroclaw School of Banking in November 2018 for useful discussions.

The authors gratefully acknowledge the two anonymous reviewers for their useful comments and suggestions that allowed to improve the paper.

Author information

Authors and Affiliations

  1. Department of Economics and Finance, LUISS University, Viale Romania 32, 00197, Rome, Italy

    Marco Dall’Aglio

  2. Department of Sciences and Innovative Technologies (DISIT), University of Eastern Piedmont, Viale T. Michel 11, 15121, Alessandria, Italy

    Vito Fragnelli

  3. Université Paris-Dauphine, PSL Research University, CNRS, LAMSADE, Place du Maréchal de Lattre de Tassigny, 75775, Paris Cedex 16, France

    Stefano Moretti

Authors
  1. Marco Dall’Aglio
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vito Fragnelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Stefano Moretti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vito Fragnelli .

Editor information

Editors and Affiliations

  1. Wroclaw University of Technology, Wroclaw, Poland

    Ngoc Thanh Nguyen

  2. Swinburne University of Technology, Hawthorn, VIC, Australia

    Ryszard Kowalczyk

  3. WSB University in Wroclaw, Wroclaw, Poland

    Jacek Mercik

  4. WSB University in Wroclaw, Wroclaw, Poland

    Anna Motylska-Kuźma

Rights and permissions

Reprints and permissions

Copyright information

© 2019 Springer-Verlag GmbH Germany, part of Springer Nature

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Dall’Aglio, M., Fragnelli, V., Moretti, S. (2019). Orders of Criticality in Graph Connection Games. In: Nguyen, N., Kowalczyk, R., Mercik, J., Motylska-Kuźma, A. (eds) Transactions on Computational Collective Intelligence XXXIV. Lecture Notes in Computer Science(), vol 11890. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-60555-4_3

Download citation

  • DOI: https://doi.org/10.1007/978-3-662-60555-4_3

  • Published:

  • Publisher Name: Springer, Berlin, Heidelberg

  • Print ISBN: 978-3-662-60554-7

  • Online ISBN: 978-3-662-60555-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics