Abstract
Entropic uncertainty relations are quantitative characterizations of Heisenberg’s uncertainty principle, which make use of an entropy measure to quantify uncertainty. We propose a new entropic uncertainty relation. It is the first such uncertainty relation that lower bounds the uncertainty in the measurement outcome for all but one choice for the measurement from an arbitrary (and in particular an arbitrarily large) set of possible measurements, and, at the same time, uses the min-entropy as entropy measure, rather than the Shannon entropy. This makes it especially suited for quantum cryptography.
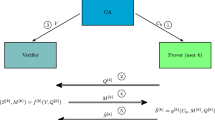
As application, we propose a new quantum identification scheme in the bounded-quantum-storage model. It makes use of our new uncertainty relation at the core of its security proof. In contrast to the original quantum identification scheme proposed by Damgård et al. [4], our new scheme also offers some security in case the bounded-quantum-storage assumption fails to hold. Specifically, our scheme remains secure against an adversary that has unbounded storage capabilities but is restricted to (non-adaptive) single-qubit operations. The scheme by Damgård et al., on the other hand, completely breaks down under such an attack.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bhatia, R.: Matrix Analysis. Springer, New York (1997)
Bouman, N.J., Fehr, S., González-Guillén, C., Schaffner, C.: An all-but-one entropic uncertainty relation, and application to password-based identification (2011), full version http://arxiv.org/abs/1105.6212
Damgård, I., Fehr, S., Salvail, L., Schaffner, C.: Cryptography in the bounded quantum-storage model. In: 46th Ann. IEEE FOCS, pp. 449–458 (2005); also in SIAM Journal on Computing 37(6),1865–1890 (2008)
Damgård, I.B., Fehr, S., Salvail, L., Schaffner, C.: Secure Identification and QKD in the Bounded-Quantum-Storage Model. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 342–359. Springer, Heidelberg (2007)
Diaconis, P.: Group Representations in Probability and Statistics. Lecture Notes — Monograph series, vol. 11. Inst. of Math. Stat., Hayward (1988)
Kittaneh, F.: Norm inequalities for certain operator sums. Journal of Functional Analysis 143(2), 337–348 (1997)
König, R., Renner, R., Schaffner, C.: The operational meaning of min-and max-entropy. IEEE Tran. Inf. Th. 55(9), 4337–4347 (2009)
Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60(12), 3 (1988)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information, 1st edn. Cambridge University Press (2000)
Renner, R.: Security of Quantum Key Distribution. PhD thesis, ETH Zürich (Switzerland) (September 2005), http://arxiv.org/abs/quant-ph/0512258
Renner, R., König, R.: Universally Composable Privacy Amplification Against Quantum Adversaries. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 407–425. Springer, Heidelberg (2005)
Schaffner, C.: Cryptography in the Bounded-Quantum-Storage Model. PhD thesis, University of Aarhus (Denmark) (September 2007)
Wehner, S., Winter, A.: Entropic uncertainty relations—a survey. New J. of Phys. 12(2) (2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Bouman, N.J., Fehr, S., González-Guillén, C., Schaffner, C. (2013). An All-But-One Entropic Uncertainty Relation, and Application to Password-Based Identification. In: Iwama, K., Kawano, Y., Murao, M. (eds) Theory of Quantum Computation, Communication, and Cryptography. TQC 2012. Lecture Notes in Computer Science, vol 7582. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-35656-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-642-35656-8_3
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-35655-1
Online ISBN: 978-3-642-35656-8
eBook Packages: Computer ScienceComputer Science (R0)