Abstract
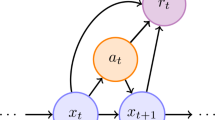
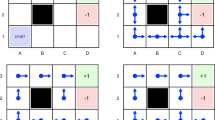
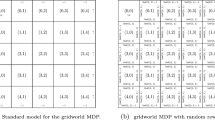
This paper describes compound reinforcement learning (RL) that is an extended RL based on the compound return. Compound RL maximizes the logarithm of expected double-exponentially discounted compound return in return-based Markov decision processes (MDPs). The contributions of this paper are (1) Theoretical description of compound RL that is an extended RL framework for maximizing the compound return in a return-based MDP and (2) Experimental results in an illustrative example and an application to finance.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Basu, A., Bhattacharyya, T., Borkar, V.S.: A learning algorithm for risk-sensitive cost. Mathematics of Operations Research 33(4), 880–898 (2008)
Borkar, V.S.: Q-learning for risk-sensitive control. Mathematics of Operations Research 27(2), 294–311 (2002)
Campbell, J.Y., Lo, A.W., Graig MacKinlay, A.: The Econometrics of Financial Markets. Princeton University Press (1997)
CMA. Global sovereign credit risk report, 4th quarter 2010. Credit Market Analysis, Ltd. (CMA) (2011)
Geibel, P., Wysotzki, F.: Risk-sensitive reinforcement learning applied to control under constraints. Journal of Artificial Intelligence Research 24, 81–108 (2005)
Gosavi, A.: A reinforcement learning algorithm based on policy iteration for average reward: Empirical results with yield management and convergence analysis. Machine Learning 55(1), 5–29 (2004)
Heger, M.: Consideration of risk in reinforcement learning. In: Proc. of the Eleventh International Conference on Machine Learning, ICML 1994, pp. 105–111 (1994)
Kelly Jr., J.L.: A new interpretation of information rate. Bell System Technical Journal 35, 917–926 (1956)
Mihatsch, O., Neuneier, R.: Risk-sensitive reinforcement learning. Machine Learning 49(2-3), 267–290 (2002)
Poundstone, W.: Fortune’s Formula: The untold story of the scientific betting system that beat the casinos and wall street. Hill and Wang (2005)
Sato, M., Kobayashi, S.: Average-reward reinforcement learning for variance penalized Markov decision problems. In: Proc. of the Eighteenth International Conference on Machine Learning, ICML 2001, pp. 473–480 (2001)
Schwartz, A.: A reinforcement learning method for maximizing undiscounted rewards. In: Proc. of the Tenth International Conference on Machine Learning (ICML 1993), pp. 298–305 (1993)
Singh, S.P.: Reinforcement learning algorithms for average-payoff Markovian decision processes. In: Proc. of the Twelfth National Conference on Artificial Intelligence (AAAI 1994), vol. 1, pp. 700–705 (1994)
Sutton, R.S., Barto, A.G.: Reinforcement Learning: An Introduction. The MIT Press (1998)
Tsitsiklis, J.N., Van Roy, B.: On average versus discounted reward temporal-difference learning. Machine Learning 49, 179–191 (2002)
Vince, R.: Portfolio management formulas: mathematical trading methods for the futures, options, and stock markets. Wiley (1990)
Watkins, C.J.C.H., Dayan, P.: Technical note: Q-learning. Machine Learning 8(3/4), 279–292 (1992)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Matsui, T., Goto, T., Izumi, K., Chen, Y. (2012). Compound Reinforcement Learning: Theory and an Application to Finance. In: Sanner, S., Hutter, M. (eds) Recent Advances in Reinforcement Learning. EWRL 2011. Lecture Notes in Computer Science(), vol 7188. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-29946-9_31
Download citation
DOI: https://doi.org/10.1007/978-3-642-29946-9_31
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-29945-2
Online ISBN: 978-3-642-29946-9
eBook Packages: Computer ScienceComputer Science (R0)