Abstract
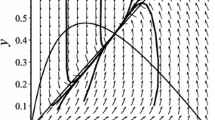
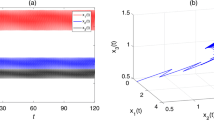
In this paper, we investigate the predator-prey system governed by impulsive differential equation with Leslie functional response. Sufficient conditions are obtained for the existence of periodic solutions. The main approach is based on Mawhin’s continuation theorem of the coincidence degree. Further, some numerical simulations demonstrate that our model can occur in many forms of complexities including periodic oscillation and chaotic strange attractor.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Xie, W.X., Wang, W.D.: Qualitative analysis of a Leslie predator-prey system with competition. Journal of Southwest University (Natural Science Edition) 31(3), 18–21 (2009)
Aziz-Alaoui, M.A.: Study of a Leslie-Gower type tritrophic population model. Chaos, Solitons Fractals 14, 1275–1293 (2002)
Liang, Z., Pan, H.: Qualitative analysis of a ratio-dependent Holling-Tanner model. J. Math. Anal. Appl. 334, 954–964 (2007)
Lu, Z.Q., Liu, X.: Analysis of a predator-prey model with modified Holling-Tanner functional response and time delay. Nonlinear Analysis. Real World Applications 9, 641–650 (2008)
Chen, Y.M., Li, Q.H., Xu, D.G.: Study on dynamics of a modified Leslie predator-prey system. Guangxi Sciences 18(1), 7–10 (2011)
Liang, Z.Q., Chen, L.S.: Stability of periodic solution for a discrete Leslie predator-prey system. Acta Mathematica Scientia 26A (2006)
Pan, H.W., Liang, Z.Q.: Existence of positive periodic solution for a Leslie system with stage structure. Mathematics in Practice and Theory 40(16), 130–137 (2010)
Liu, X., Chen, L.S.: Global dynamics of the periodic logistic system with periodic impulsive perturbations. J. Math. Anal. Appl. 289, 279–291 (2010)
Gaines, R.E., Mawhin, J.L.: Coincidence degree and nonlinear differential equations. Springer, Berlin (1977)
Zhang, J., Gui, Z.J.: Periodic solutions of nonautonomous cellular neural networks with impulses and delays. Nonlinear Analysis: Real World Applications 10, 1891–1903 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, K., Zhang, W., Gui, Z. (2011). The Existence and Simulations of Periodic Solution of Leslie Predator-Prey Model with Impulsive Perturbations. In: Liu, C., Chang, J., Yang, A. (eds) Information Computing and Applications. ICICA 2011. Communications in Computer and Information Science, vol 244. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-27452-7_16
Download citation
DOI: https://doi.org/10.1007/978-3-642-27452-7_16
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-27451-0
Online ISBN: 978-3-642-27452-7
eBook Packages: Computer ScienceComputer Science (R0)