Abstract
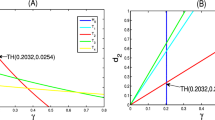
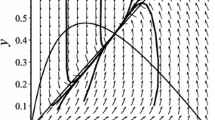
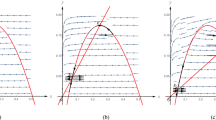
The principle aim of this paper is to explore the existence of periodic solution of a Leslie-Gower predator-prey model with impulsive perturbations. Sufficient and realistic conditions are obtained by using Mawhin’s continuation theorem of the coincidence degree. Further, some numerical simulations show that our model can occur in many forms of complexities including periodic oscillation and chaotic strange attractor.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Liu, K.Y.: Dynamic behaviors of a Leslie-Gower predator-prey model with birth pulse. Journal of Biomathematics 23(3), 390–398 (2008)
Leslie, P.H.: A Stochastic model for studying the properties of certain biological systems by numerical methods. Biometika 45(1), 16–31 (1958)
Zhang, J., Wang, K.: On the persistence of a Leslie system in a polluted environment. Journal of Biomathematics 21(4), 501–508 (2006)
Liu, H.X.: Dynamic properties analysis of a modified Leslie-Gower type preypredator systems. Journal of Guangdong Ocean University 29(3), 53–58 (2009)
Li, Z.: Permanence and global attractivity of a predator-prey model with modified Leslie-Gower and Holling type II schemes with feedback controls. Mathematics in Practice and Theory 41(7), 126–130 (2011)
Zhang, L.M.: Stability and bifurcation in a discrete predator-prey system with Leslie-Gower type. Sichuan University of Arts and Science Journal 20(2), 13–15 (2010)
Aziz-Alaoui, M.A., Daher Okiye, M.: Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling type II schemes. Applied Mathematics Letters 16, 1069–1075 (2003)
Gaines, R.E., Mawhin, J.L.: Coincidence degree and nonlinear differential equations. Springer, Berlin (1977)
Zhang, J., Gui, Z.J.: Existence and stability of periodic solutions of high-order Hopfield neural networks with impulses and delays. Journal of Computational and Applied Mathematics 224, 602–613 (2009)
Zhang, J., Gui, Z.J.: Periodic solutions of nonautonomous cellular neural networks with impulses and delays. Nonlinear Analysis: Real World Applications 10, 1891–1903 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, K., Gui, Z. (2011). The Existence and Simulations of Periodic Solutions of a Leslie-Gower Predator-Prey Model with Impulsive Perturbations. In: Liu, C., Chang, J., Yang, A. (eds) Information Computing and Applications. ICICA 2011. Communications in Computer and Information Science, vol 244. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-27452-7_15
Download citation
DOI: https://doi.org/10.1007/978-3-642-27452-7_15
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-27451-0
Online ISBN: 978-3-642-27452-7
eBook Packages: Computer ScienceComputer Science (R0)