Abstract
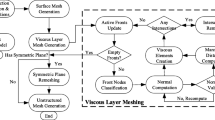
This paper presents a robust and automated approach to generate unstructured hybrid grids comprised of prismatic and tetrahedral elements for viscous flow computations. The hybrid mesh generation starts from a triangulated surface mesh. The prismatic elements are extruded based on the weak solutions of the Eikonal equation to generate anisotropic elements at boundaries, and finally the isotropic tetrahedral grids are generated to fill the rest of the domain. The presented hybrid meshing algorithm was validated using a ball valve model under both steady and unsteady conditions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
1. Y. L.Wang, F. Guibault, R. Camarero, and K. -F. Tchon, “A parametrization transporting surface offset construction method based on the eikonal equation,” in 17th AIAA CFD Conf., June 2005.
2. H. K. Zhao, “A fast sweeping method for eikonal equations,” Mathematics of Computation, vol. 74, no. 250, pp. 603–627, 2005.
3. J. Hoffman, Numerical Methods for Engineers and Scientists. McGraw-Hill Inc., 1992.
4. H. Borouchaki, Hecht, F., E. Saltel and P. L. George, “Reasonably Eficient Delaunay Based Mesh Generator in 3 Dimensions,“ in Proceedings 4th International Meshing Roundtable, Sandia National Laboratories, pp. 3–14, 1995
5. Y. L. Wang, F. Guibault, and R. Camarero, “Automatic near-body domain decomposition using the eikonal equation,“ in Proceedings of the 14th International Meshing Roundtable, Sandia National Laboratory, Sept. 2005.
6. Y. L. Wang, F. Guibault, and R. Camarero (2006) Int. J. Numer. Meth. Engng, Submitted.
7. P. L. George, F. Hecht, and E. Saltel, “Automatic Mesh Generator with Specified Boundary,“ in Computer Methods in Applied Mechanics and Engineering, North-Holland, Vol 92, pp. 269–288, 1991
8. F. Guibault, Un mailleur hybride structuré/non structuré en trois dimensions. PhD thesis, école Polytechnique de Montréal, 1998.
9. S. Pirzadeh, “Unstructured viscous grid generation by advancing-layers method,” in AIAA 11th Applied Aerodynamics Conference, no. AIAA-93-3453, (Monterey, CA), pp. 420–434, Aug. August 9-11, 1993.
10. J. Suillivan and J. Zhang, “Adaptive mesh generation using a normal offsetting technique,” Finite Elements in Analysis and Design, vol. 25, pp. 275–295, 1997.
11. J. Glimm, J. Grove, X. Li, and D. Tan, “Robust computational algorithms for dynamic interface tracking in three dimensions,” SIAM J. Sci. Comp., vol. 21, no. 6, pp. 2240–2256, 2000.
12. R. Blomgren, “B-spline curves, boeing document, class notes, b-7150-bb-wp-2811d-4412,” 1981.
13. W. Tiller and E. Hanson, “offsets of two-dimensional profiles,” IEEE Computer Graphics and Applications, vol. 4, no. 9, pp. 36–46, 1984.
14. S. Coquillart, “Computing offsets of b-spline curves,” Comp.-Aided Design, vol. 19, no. 6, pp. 305–309, 1987.
15. A. Kulczycka and L. Nachman, “Qualitative and quantitative comparisons of b-spline offset surface approximation methods,” Comp.-Aided Design, vol. 34, pp. 19–26, Jan. 2002.
16. L. A. Piegl and W. Tiller, “Computing offsets of nurbs curves and surfaces,” Comp.-Aided Design, vol. 31, pp. 147–156, Feb. 1999.
17. Y. F. Sun, A. Y. C. M. Nee, and K. S. Lee, “Modifying free-formed nurbs curves and surfaces for offsetting without local self-intersection,” Comp.-Aided Design, vol. 36, no. 12, pp. 1161–1169, 2004.
18. R. T. Farouki, “The approximation of non-degenerate offset surfaces,” Comp.-Aided Geom. Design, vol. 3, no. 1, pp. 15–43, 1986.
19. S. Osher and J. A. Sethian, “Fronts propagating with curvature-dependent speed: Algorithms based on hamilton-jacobi formulations,” J. Comp. Phys., vol. 79, pp. 12–49, 1988.
20. J. A. Sethian, “A fast marching level set method for monotonically advancing fronts,” Proceedings of the National Academy of Sciences of the United States of America, vol. 93, no. 4, pp. 1591–1595, 1996.
21. J. A. Sethian, Level set methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press, 1999.
22. J. A. Sethian, “Fast marching methods,” SIAM Review, vol. 41, no. 2, pp. 199–235, 1999.
23. T. D. Blacker and M. B. Stephenson, “Paving: A new approach to Automated Quardrilateral Mesh Generation,” SIAM Journal on Numerical Analysis, vol. 32, pp. 811–847, 1991.
24. R. J. Cass and S. E. Benzley and R. J. Meyers and T. D. Blacker, “Generalized 3-D Paving: An Automated Quadrilateral Surface Mesh Generation Algorithm,” SIAM Journal on Numerical Analysis, vol. 39, no. 9, pp. 1475–1489, 1998.
25. “TGrid 3.5 User's Manual,” Fluent Inc., April, 2003.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer
About this paper
Cite this paper
Wang, Y., Murgie, S. (2006). Hybrid Mesh Generation for Viscous Flow Simulation. In: Pébay, P.P. (eds) Proceedings of the 15th International Meshing Roundtable. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-34958-7_7
Download citation
DOI: https://doi.org/10.1007/978-3-540-34958-7_7
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-34957-0
Online ISBN: 978-3-540-34958-7
eBook Packages: EngineeringEngineering (R0)