Abstract
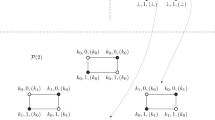
We propose several self-stabilizing protocols for unidirectional, anonymous, and uniform synchronous rings of arbitrary size, where processors communicate by exchanging messages. When the size of the ring n is unknown, we better the service time by a factor of n (performing the best possible complexity for the stabilization time and the memory consumption). When the memory size is known, we present a protocol that is optimal in memory (constant and independant of n), stabilization time, and service time (both are in Θ(n)).
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Beauquier, J., Cordier, S., Delaët, S.: Optimum probabilistic selfstabilization on uniform rings. In: WSS 1995 Second Workshop on Self-Stabilizing Systems, pp. 15.1–15.15 (1995)
Beauquier, J., Gradinariu, M., Johnen, C.: Memory space requirements for self-stabilizing leader election protocols. In: PODC 1999 18th Annual ACM Symposium on Principles of Distributed Computing, pp. 199–208 (1999)
Burns, J.E., Pachl, J.: Uniform self-stabilizing rings. ACM Transactions on Programming Languages and Systems 11(2), 330–344 (1989)
Duflot, M., Fribourg, L., Picaronny, C.: Finite-state distributed algorithms as markov chains. In: Welch, J.L. (ed.) DISC 2001. LNCS, vol. 2180, pp. 240–255. Springer, Heidelberg (2001)
Datta, A.K., Gradinariu, M., Tixeuil, S.: Self-stabilizing mutual exclusion using unfair distributed scheduler. In: IPDPS 2000 14th International Parallel and Distributed Processing Symposium, pp. 465–470 (2000)
Dijkstra, E.W.: Self stabilizing systems in spite of distributed control. Communications of the ACM 17(11), 643–644 (1974)
Dolev, S.: Self-stabilization. The MIT Press, Cambridge (2000)
Fribourg, L., Messika, S., Picaronny, C.: Coupling and self-stabilization. In: Guerraoui, R. (ed.) DISC 2004. LNCS, vol. 3274, pp. 201–215. Springer, Heidelberg (2004)
Herman, T.: Probabilistic self-stabilization. Information Processing Letters 35(2), 63–67 (1990)
Johnen, C.: Service time optimal self-stabilizing token circulation protocol on anonymous unidrectional rings. In: SRDS 2002 21th Symposium on Reliable Distributed Systems, pp. 80–89. IEEE Computer Society Press, Los Alamitos (2002)
Katz, S., Perry, K.J.: Self-stabilizing extensions for message-passing systems. Distributed Computing 7(1), 17–26 (1993)
Kakugawa, H., Yamashita, M.: Uniform and self-stabilizing fair mutual exclusion on unidirectional rings under unfair distributed daemon. Journal of Parallel and Distributed Computing 62(5), 885–898 (2002)
Norris, J.R.: Markov Chains. Cambridge University Press, Cambridge (1997)
Rosaz, L.: Self-stabilizing token circulation on asynchronous uniform unidirectional rings. In: PODC 2000 19th Annual ACM Symposium on Principles of Distributed Computing, pp. 249–258 (2000)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2004 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Duchon, P., Hanusse, N., Tixeuil, S. (2004). Optimal Randomized Self-stabilizing Mutual Exclusion on Synchronous Rings. In: Guerraoui, R. (eds) Distributed Computing. DISC 2004. Lecture Notes in Computer Science, vol 3274. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30186-8_16
Download citation
DOI: https://doi.org/10.1007/978-3-540-30186-8_16
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-23306-0
Online ISBN: 978-3-540-30186-8
eBook Packages: Springer Book Archive