Buffering Gene Expression Noise by MicroRNA Based Feedforward Regulation | SpringerLink
Skip to main content
Springer Nature Link
Log in

Buffering Gene Expression Noise by MicroRNA Based Feedforward Regulation

  • Conference paper
  • First Online:
Computational Methods in Systems Biology (CMSB 2018)

Part of the book series: Lecture Notes in Computer Science ((LNBI,volume 11095))

Included in the following conference series:

  • 844 Accesses

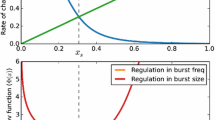
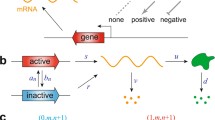
Abstract

Cells use various regulatory motifs, including feedforward loops, to control the intrinsic noise that arises in gene expression at low copy numbers. Here we study one such system, which is broadly inspired by the interaction between an mRNA molecule and an antagonistic microRNA molecule encoded by the same gene. The two reaction species are synchronously produced, individually degraded, and the second species (microRNA) exerts an antagonistic pressure on the first species (mRNA). Using linear-noise approximation, we show that the noise in the first species, which we quantify by the Fano factor, is sub-Poissonian, and exhibits a nonmonotonic response both to the species lifetime ratio and to the strength of the antagonistic interaction. Additionally, we use the Chemical Reaction Network Theory to prove that the first species distribution is Poissonian if the first species is much more stable than the second. Finally, we identify a special parametric regime, supporting a broad range of behaviour, in which the distribution can be analytically described in terms of the confluent hypergeometric limit function. We verify our analysis against large-scale kinetic Monte Carlo simulations. Our results indicate that, subject to specific physiological constraints, optimal parameter values can be found within the mRNA–microRNA motif that can benefit the cell by lowering the gene-expression noise.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 6863
Price includes VAT (Japan)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 8579
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Abou-Jaoudé, W., Thieffry, D., Feret, J.: Formal derivation of qualitative dynamical models from biochemical networks. Biosystems 149, 70–112 (2016)

    Article  Google Scholar 

  2. Abramowitz, M., Stegun, I.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards, Washington, D.C. (1972)

    MATH  Google Scholar 

  3. Alon, U.: Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461 (2007)

    Article  Google Scholar 

  4. Anderson, D.F., Cotter, S.L.: Product-form stationary distributions for deficiency zero networks with non-mass action kinetics. Bull. Math. Biol. 78, 2390–2407 (2016)

    Article  MathSciNet  Google Scholar 

  5. Anderson, D.F., Craciun, G., Kurtz, T.G.: Product-form stationary distributions for deficiency zero chemical reaction networks. Bull. Math. Biol. 72, 1947–1970 (2010)

    Article  MathSciNet  Google Scholar 

  6. Bleris, L., Xie, Z., Glass, D., Adadey, A., Sontag, E., Benenson, Y.: Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template. Mol. Syst. Biol. 7, 519 (2011)

    Article  Google Scholar 

  7. Bokes, P., King, J., Wood, A., Loose, M.: Multiscale stochastic modelling of gene expression. J. Math. Biol. 65, 493–520 (2012)

    Article  MathSciNet  Google Scholar 

  8. Bokes, P., Lin, Y., Singh, A.: High cooperativity in negative feedback can amplify noisy gene expression. Bull. Math. Biol. (2018). https://doi.org/10.1007/s11538-018-0438-y

  9. Bokes, P., King, J.R., Wood, A.T., Loose, M.: Exact and approximate distributions of protein and mRNA levels in the low-copy regime of gene expression. J. Math. Biol. 64, 829–854 (2012)

    Article  MathSciNet  Google Scholar 

  10. Bokes, P., Singh, A.: Gene expression noise is affected differentially by feedback in burst frequency and burst size. J. Math. Biol. 74, 1483–1509 (2017)

    Article  MathSciNet  Google Scholar 

  11. Bosia, C., Osella, M., Baroudi, M.E., Cora, D., Caselle, M.: Gene autoregulation via intronic microRNAs and its functions. BMC Syst. Biol. 6, 131 (2012)

    Article  Google Scholar 

  12. Bronstein, L., Koeppl, H.: A variational approach to moment-closure approximations for the kinetics of biomolecular reaction networks. J. Chem. Phys. 148, 014105 (2018)

    Article  Google Scholar 

  13. Cardelli, L., Kwiatkowska, M., Laurenti, L.: Stochastic analysis of chemical reaction networks using linear noise approximation. Biosystems 149, 26–33 (2016)

    Article  Google Scholar 

  14. Cinquemani, E.: On observability and reconstruction of promoter activity statistics from reporter protein mean and variance profiles. In: Cinquemani, E., Donzé, A. (eds.) HSB 2016. LNCS, vol. 9957, pp. 147–163. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-47151-8_10

    Chapter  Google Scholar 

  15. Feinberg, M.: Lectures on chemical reaction networks. Notes of lectures given at the Mathematics Research Center of the University of Wisconsin (1979)

    Google Scholar 

  16. Ghusinga, K.R., Vargas-Garcia, C.A., Lamperski, A., Singh, A.: Exact lower and upper bounds on stationary moments in stochastic biochemical systems. Phys. Biol. 14, 04LT01 (2017)

    Article  Google Scholar 

  17. Gillespie, D.: A general method for numerically simulating stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434 (1976)

    Article  MathSciNet  Google Scholar 

  18. Herath, N., Del Vecchio, D.: Reduced linear noise approximation for biochemical reaction networks with time-scale separation: the stochastic tQSSA+. J. Chem. Phys. 148, 094108 (2018)

    Article  Google Scholar 

  19. Innocentini, G.C., Forger, M., Radulescu, O., Antoneli, F.: Protein synthesis driven by dynamical stochastic transcription. Bull. Math. Biol. 78, 110–131 (2016)

    Article  MathSciNet  Google Scholar 

  20. Innocentini, G.C., Guiziou, S., Bonnet, J., Radulescu, O.: Analytic framework for a stochastic binary biological switch. Phys. Rev. E 94, 062413 (2016)

    Article  Google Scholar 

  21. Johnson, N., Kotz, S., Kemp, A.: Univariate Discrete Distributions, 3rd edn. Wiley, Hoboken (2005)

    Book  Google Scholar 

  22. van Kampen, N.: Stochastic Processes in Physics and Chemistry. Elsevier, New York (2006)

    MATH  Google Scholar 

  23. Kan, X., Lee, C.H., Othmer, H.G.: A multi-time-scale analysis of chemical reaction networks: II. Stochastic systems. J. Math. Biol. 73, 1081–1129 (2016)

    Article  MathSciNet  Google Scholar 

  24. Kelly, F.P.: Reversibility and Stochastic Networks. Cambridge University Press, Cambridge (2011)

    MATH  Google Scholar 

  25. Kim, J.K., Josić, K., Bennett, M.R.: The validity of quasi-steady-state approximations in discrete stochastic simulations. Biophys. J. 107, 783–793 (2014)

    Article  Google Scholar 

  26. Kumar, N., Jia, T., Zarringhalam, K., Kulkarni, R.V.: Frequency modulation of stochastic gene expression bursts by strongly interacting small RNAs. Phys. Rev. E 94, 042419 (2016)

    Article  Google Scholar 

  27. Kurtz, T.G.: The relationship between stochastic and deterministic models for chemical reactions. J. Chem. Phys. 57, 2976–2978 (1972)

    Article  Google Scholar 

  28. Lestas, I., Paulsson, J., Ross, N., Vinnicombe, G.: Noise in gene regulatory networks. IEEE Trans. Circuits-I 53, 189–200 (2008)

    MathSciNet  MATH  Google Scholar 

  29. Li, X., Cassidy, J.J., Reinke, C.A., Fischboeck, S., Carthew, R.W.: A microRNA imparts robustness against environmental fluctuation during development. Cell 137, 273–282 (2009)

    Article  Google Scholar 

  30. Maarleveld, T.R., Olivier, B.G., Bruggeman, F.J.: StochPy: a comprehensive, user-friendly tool for simulating stochastic biological processes. PLoS One 8, e79345 (2013)

    Article  Google Scholar 

  31. Mastny, E., Haseltine, E., Rawlings, J.: Two classes of quasi-steady-state model reductions for stochastic kinetics. J. Chem. Phys. 127, 094106 (2007)

    Article  Google Scholar 

  32. Nevozhay, D., Adams, R.M., Murphy, K.F., Josic, K., Balazsi, G.: Negative autoregulation linearizes the dose response and suppresses the heterogeneity of gene expression. Proc. Natl. Acad. Sci. U.S.A. 106, 5123–5128 (2009)

    Article  Google Scholar 

  33. Osella, M., Bosia, C., Corá, D., Caselle, M.: The role of incoherent microRNA-mediated feedforward loops in noise buffering. PLoS Comput. Biol. 7, e1001101 (2011)

    Article  Google Scholar 

  34. Paulsson, J.: Models of stochastic gene expression. Phys. Life Rev. 2, 157–175 (2005)

    Article  Google Scholar 

  35. Platini, T., Jia, T., Kulkarni, R.V.: Regulation by small RNAs via coupled degradation: Mean-field and variational approaches. Phys. Rev. E 84, 021928 (2011)

    Article  Google Scholar 

  36. Popovic, N., Marr, C., Swain, P.S.: A geometric analysis of fast-slow models for stochastic gene expression. J. Math. Biol. 72, 87–122 (2016)

    Article  MathSciNet  Google Scholar 

  37. Schmiedel, J.M., et al.: MicroRNA control of protein expression noise. Science 348, 128–132 (2015)

    Article  Google Scholar 

  38. Singh, A.: Negative feedback through mRNA provides the best control of gene-expression noise. IEEE Trans. NanoBiosci. 10, 194–200 (2011)

    Article  Google Scholar 

  39. Singh, A., Bokes, P.: Consequences of mRNA transport on stochastic variability in protein levels. Biophys. J. 103, 1087–1096 (2012)

    Article  Google Scholar 

  40. Singh, A., Vargas-Garcia, C.A., Karmakar, R.: Stochastic analysis and inference of a two-state genetic promoter model. In: Proceedings of the American Control Conference, pp. 4563–4568 (2013)

    Google Scholar 

  41. Singh, A., Grima, R.: The linear-noise approximation and moment-closure approximations for stochastic chemical kinetics. arXiv preprint arXiv:1711.07383 (2017)

  42. Singh, A., Hespanha, J.P.: Optimal feedback strength for noise suppression in autoregulatory gene networks. Biophys. J. 96, 4013–4023 (2009)

    Article  Google Scholar 

  43. Soltani, M., Platini, T., Singh, A.: Stochastic analysis of an incoherent feedforward genetic motif. In: American Control Conference (ACC), pp. 406–411 (2016)

    Google Scholar 

  44. Srivastava, R., Haseltine, E.L., Mastny, E., Rawlings, J.B.: The stochastic quasi-steady-state assumption: reducing the model but not the noise. J. Chem. Phys. 134, 154109 (2011)

    Article  Google Scholar 

  45. Stewart, A.J., Seymour, R.M., Pomiankowski, A., Reuter, M.: Under-dominance constrains the evolution of negative autoregulation in diploids. PLoS Comput. Biol. 9, e1002992 (2013)

    Article  Google Scholar 

  46. Strovas, T.J., Rosenberg, A.B., Kuypers, B.E., Muscat, R.A., Seelig, G.: MicroRNA-based single-gene circuits buffer protein synthesis rates against perturbations. ACS Synth. Biol. 3, 324–331 (2014)

    Article  Google Scholar 

  47. Veerman, F., Marr, C., Popović, N.: Time-dependent propagators for stochastic models of gene expression: an analytical method. J. Math. Biol. (2018). https://doi.org/10.1007/s00285-017-1196-4

  48. Voliotis, M., Bowsher, C.G.: The magnitude and colour of noise in genetic negative feedback systems. Nucleic Acids Res. 40, 7084–7095 (2012)

    Article  Google Scholar 

  49. Yang, X., Wu, Y., Yuan, Z.: Characteristics of mRNA dynamics in a multi-on model of stochastic transcription with regulation. Chin. J. Phys. 55, 508–518 (2017)

    Article  Google Scholar 

Download references

Acknowledgements

PB acknowledges support from the Slovak Research and Development Agency under the contract No. APVV-14-0378, the VEGA grant 1/0347/18, and the EraCoSysMed project 4D-Healing. AS is supported by the National Science Foundation grant ECCS-1711548.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics and Statistics, Comenius University, 84248, Bratislava, Slovakia

    Pavol Bokes & Michal Hojcka

  2. Mathematical Institute, Slovak Academy of Sciences, 81473, Bratislava, Slovakia

    Pavol Bokes

  3. Department of Electrical and Computer Engineering, University of Delaware, Newark, DE, 19716, USA

    Abhyudai Singh

Authors
  1. Pavol Bokes
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michal Hojcka
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abhyudai Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pavol Bokes .

Editor information

Editors and Affiliations

  1. Brno University of Technology, Brno, Czech Republic

    Milan Češka

  2. Masaryk University, Brno, Czech Republic

    David Šafránek

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Bokes, P., Hojcka, M., Singh, A. (2018). Buffering Gene Expression Noise by MicroRNA Based Feedforward Regulation. In: Češka, M., Šafránek, D. (eds) Computational Methods in Systems Biology. CMSB 2018. Lecture Notes in Computer Science(), vol 11095. Springer, Cham. https://doi.org/10.1007/978-3-319-99429-1_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-99429-1_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-99428-4

  • Online ISBN: 978-3-319-99429-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics