Abstract
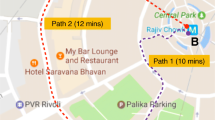
Input to the Most Navigable Path (MNP) problem consists of the following: (a) a road network represented as a directed graph, where each edge is associated with numeric attributes of cost and “navigability score” values; (b) a source and a destination and; (c) a budget value which denotes the maximum permissible cost of the solution. Given the input, MNP aims to determine a path between the source and the destination which maximizes the navigability score while constraining its cost to be within the given budget value. This problem finds its applications in navigation systems for developing nations where streets, quite often, do not display their names. MNP problem would help in such cases by providing routes which are more convenient for a driver to identify and follow. Our problem is modeled as the arc orienteering problem which is known to be NP-hard. The current state-of-the-art for this problem may generate paths having loops, and its adaptation for MNP, that yields simple paths, was found to be inefficient. In this paper, we propose two novel algorithms for the MNP problem. Our experimental results indicate that the proposed solutions yield comparable or better solutions while being orders of magnitude faster than the current state-of-the-art for large real road networks. We also propose an indexing structure for the MNP problem which significantly reduces the running time of our algorithms.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
If the edge costs represent travel-times, then a lower bound on the travel time may be used. This can be computed using the upper speed limit of a road segment.
- 2.
Best-successor in case of forward search and best-predecessor in case of backward search.
- 3.
If edge costs represent travel-times, then the travel-time based budget can be converted to a distance based budget using the upper speed limit of a road segment.
References
Aly, A.M., et al.: AQWA: adaptive query workload aware partitioning of big spatial data. Proc. VLDB Endow. 8(13), 2062–2073 (2015)
Archetti, C., Corberán, A., Plana, I., Sanchis, J.M., Speranza, M.G.: A branch-and-cut algorithm for the orienteering arc routing problem. Comput. Oper. Res. 66(C), 95–104 (2016)
Bolzoni, P., Helmer, S.: Hybrid best-first greedy search for orienteering with category constraints. In: Gertz, M., et al. (eds.) SSTD 2017. LNCS, vol. 10411, pp. 24–42. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-64367-0_2
Bolzoni, P., Persia, F., Helmer, S.: Itinerary planning with category constraints using a probabilistic approach. In: Benslimane, D., Damiani, E., Grosky, W.I., Hameurlain, A., Sheth, A., Wagner, R.R. (eds.) DEXA 2017. LNCS, vol. 10439, pp. 363–377. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-64471-4_29
Chekuri, C., Pal, M.: A recursive greedy algorithm for walks in directed graphs. In: Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2005, pp. 245–253 (2005)
Delling, D., Goldberg, A.V., Nowatzyk, A., Werneck, R.F.: Phast: hardware-accelerated shortest path trees. J. Parallel Distrib. Comput. 73(7), 940–952 (2013)
Gavalas, D., Konstantopoulos, C., Mastakas, K., Pantziou, G., Vathis, N.: Approximation algorithms for the arc orienteering problem. Inf. Process. Lett. 115(2), 313–315 (2015)
Jing, N., Huang, Y.W., Rundensteiner, E.A.: Hierarchical encoded path views for path query processing: an optimal model and its performance evaluation. IEEE Trans. Knowl. Data Eng. 10, 409–432 (1998)
Kanoulas, E., Du, Y., Xia, T., Zhang, D.: Finding fastest paths on a road network with speed patterns. In: 22nd International Conference on Data Engineering (ICDE 2006), p. 10, April 2006
Kriegel, H.P., Renz, M., Schubert, M.: Route skyline queries: a multi-preference path planning approach. In: 2010 IEEE 26th International Conference on Data Engineering (ICDE 2010), pp. 261–272 (2010)
Lu, Y., Shahabi, C.: An arc orienteering algorithm to find the most scenic path on a large-scale road network. In: Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, pp. 46:1–46:10 (2015)
Martins, E., Pascoal, M.: A new implementation of Yen’s ranking loopless paths algorithm. Q. J. Belg. French Ital. Oper. Res. Soc. 1(2), 121–133 (2003)
Singh, A., Krause, A., Guestrin, C., Kaiser, W., Batalin, M.: Efficient planning of informative paths for multiple robots. In: Proceedings of the 20th International Joint Conference on Artificial Intelligence, IJCAI 2007, pp. 2204–2211 (2007)
Souffriau, W., Vansteenwegen, P., Berghe, G.V., Oudheusden, D.V.: The planning of cycle trips in the province of east flanders. Omega 39(2), 209–213 (2011)
Vansteenwegen, P., Souffriau, W., Oudheusden, D.V.: The orienteering problem: a survey. Eur. J. Oper. Res. 209(1), 1–10 (2011)
Verbeeck, C., Vansteenwegen, P., Aghezzaf, E.H.: An extension of the arc orienteering problem and its application to cycle trip planning. Transp. Res. Part E: Logist. Transp. Rev. 68, 64–78 (2014)
Acknowledgements
This work was in part supported by the Infosys Centre for Artificial Intelligence at IIIT-Delhi, Visvesvaraya Ph.D. Scheme for Electronics and IT, and DST SERB (ECR/2016/001053).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Kaur, R., Goyal, V., Gunturi, V.M.V. (2018). Finding the Most Navigable Path in Road Networks: A Summary of Results. In: Hartmann, S., Ma, H., Hameurlain, A., Pernul, G., Wagner, R. (eds) Database and Expert Systems Applications. DEXA 2018. Lecture Notes in Computer Science(), vol 11029. Springer, Cham. https://doi.org/10.1007/978-3-319-98809-2_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-98809-2_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-98808-5
Online ISBN: 978-3-319-98809-2
eBook Packages: Computer ScienceComputer Science (R0)