A Randomized FPT Approximation Algorithm for Maximum Alternating-Cycle Decomposition with Applications

Abstract

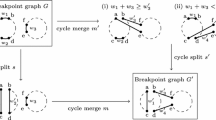
Comparing genomes in terms of gene order is a classical combinatorial optimization problem in computational biology. Some of the popular distances include translocation, reversal, and double-cut-and-join (abbreviated as DCJ), which have been extensively used while comparing two genomes. Let $d_x$, $x\in \{$translocation, reversal, DCJ$\}$, be the distance between two genomes such that one can be sorted/converted into the other using the minimum number of x-operations. All these problems are NP-hard when the genomes are unsigned. Computing $d_x$, $x\in \{$translocation, reversal, DCJ$\}$, between two unsigned genomes involves computing a proper alternating cycle decomposition of its breakpoint graph, which becomes the bottleneck for computing the genomic distance under almost all types of genome rearrangement operations and prohibits to obtain approximation factors better than 1.375 in polynomial time. In this paper, we devise an FPT (fixed-parameter tractable) approximation algorithm for computing the DCJ and translocation distances with an approximation factor 4/3+$\varepsilon$, and the running time is $O^*(2^{d^*})$, where $d^*$ represents the optimal DCJ or translocation distance. The algorithm is randomized and it succeeds with a high probability. This technique is based on a new randomized method to generate approximate maximum alternating cycle decomposition.