Abstract
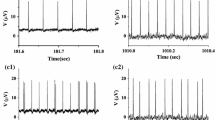
The integer multiple firing patterns, generated in the rabbit depressor baroreceptors under the different static blood pressure, were observed between the resting state and the periodic firing and were characterized to be stochastic but not chaotic by a series of nonlinear time series estimations. These patterns exhibited very similar characteristics to those observed in the experimental neural pacemaker. Using I na,p + I K models with dynamics of a supercritical Hopf bifurcation, we successfully simulated the bifurcation process of firing patterns and observed the induction of the integer multiple firing patterns by adding noise. The results strongly suggest that the integer multiple firing rhythms generated by rabbit baroreceptors result from the interplay between noise and the system’s dynamics. Because of the important normal physiological function of baroreceptors, the biological significance of noise and the noise-induced firing rhythms at a Hopf bifurcation is interesting to be addressed.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bashkirtseva, I., Ryashko, L., Slepukhina, E.: Order and chaos in the stochastic Hindmarsh-Rose model of the neuron bursting. Nonlinear Dyn. 82(1–2), 919–932 (2015)
Xing, J.L., Hu, S.J., Yang, J.: Electrophysiological features of neurons in the mesencephalic trigeminal nuclei. Neuro-Signals (22), 79–91 (2015)
Abbasi, S., Abbasi, A., Sarbaz, Y., Janahmadi, M.: Power spectral density analysis of Purkinje cell tonic and burst firing patterns from a rat model of ataxia and riluzole treated. Basic Clin. Neurosci. 8(1), 61–68 (2017)
Lu, T., Wade, K., Hong, H., Sanchez, J.T.: Ion channel mechanisms underlying frequency-firing patterns of the avian nucleus magnocellularis: a computational model. Channels (3), 1–15 (2017)
Li, Y., Gu, H.: The distinct stochastic and deterministic dynamics between period-adding and period-doubling bifurcations of neural bursting patterns. Nonlinear Dyn. 87(4), 2541–2562 (2017)
Bashkirtseva, I., Ryashko, L.: Stochastic sensitivity analysis of noise-induced order-chaos transitions in discrete-time systems with tangent and crisis bifurcations. Physica A: Stat. Mech. Appl. (467), 573–584 (2017)
Zhao, Z., Jia, B., Gu, H.: Bifurcations and enhancement of neuronal firing induced by negative feedback. Nonlinear Dyn. 86(3), 1–12 (2016)
Yang, M.H., Liu, Z.Q., Li, L., Xu, Y.L., Liu, H.J., Gu, H.G.: Identifying distinct stochastic dynamics from chaos: a study on multimodal neural firing patterns. Int. J. Bifurc. Chaos (19), 453–485 (2009)
Jia, B., Gu, H.G.: Identifying type I excitability using dynamics of stochastic neural firing patterns. Cogn. Neurodyn. (6), 485–497 (2012)
Hu, G., Ditzinger, T., Ning, C.Z.: Stochastic resonance without external periodic force. Phys. Rev. Lett. (71), 807–810 (1993)
Gu, H.G., Zhang, H.M., Wei, C.L., Yang, M.H., Liu, Z.Q., Ren, W.: Coherence resonance induced stochastic neural firing at a saddle-node bifurcation. Int. J. Mod. Phys. B (25), 3977–3986 (2011)
Azevedo, R.T., Garfinkel, S.N., Critchley, H.D., Tsakiris, M.: Cardiac afferent activity modulates the expression of racial stereotypes. Nat. Commun. (8), 13854 (2017)
Izhikevich, E.M., Edelman, G.M.: Large-scale model of mammalian thalamocortical systems. Proc. Natl. Acad. Sci. U.S.A. 105(9), 3593–3598 (2008)
Mannella, R., Palleschi, V.V.: Mean first-passage time in a bistable system driven by strongly correlated noise: introduction of a fluctuating potential. Phys. Rev. A 39(7), 3751–3753 (1989)
Huaguang, G., Zhiguo, Z., Bing, J., Shenggen, C.: Dynamics of on-off neural firing patterns and stochastic effects near a sub-critical Hopf bifurcation. Plos One 10(4), e0121028 (2015)
Xing, J.L., Hu, S.J., Xu, H., Han, S., Wan, Y.H.: Subthreshold membrane oscillations underlying integer multiples firing from injured sensory neurons. NeuroReport (12), 1311–1313 (2011)
Chay, T.R.: Chaos in a three-variable modle of an excitable cell. Physica D Nonlinear Phenom. 16(2), 233–242 (1985)
Sancristóbal, B., Rebollo, B., Boada, P., Sanchezvives, M.V., Garciaojalvo, J.: Collective stochastic coherence in recurrent neuronal networks. Nat. Phys. (12), 881–888 (2016)
Lai, Y.C., Park, K.: Noise-sensitive measure for stochastic resonance in biological oscillators. Math. Biosci. Eng. 3(4), 583–602 (2006)
Acknowledgment
This research was supported by the National Key Research And Development Program of China (No. 2016YFC0106000), the Natural Science Foundation of China (Grant No. 61302128), and the Youth Science and Technology Star Program of Jinan City (201406003), although supported by NSFC (Grant Nos. 61573166, 61572230, 61671220, 61640218), the Natural Science Foundation of Shandong Province (ZR2013FL002), the Shandong Distinguished Middle-aged and Young Scientist Encourage and Reward Foundation, China (Grant No. ZR2016FB14), the Project of Shandong Province Higher Educational Science and Technology Program, China (Grant Nos. J16LN07, J16LBO6, J17KA047), the Shandong Province Key Research and Development Program, China (Grant No. 2016GGX101022).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Shang, H., Xu, R., Wang, D., Zhou, J., Han, S. (2017). A Stochastic Neural Firing Generated at a Hopf Bifurcation and Its Biological Relevance. In: Liu, D., Xie, S., Li, Y., Zhao, D., El-Alfy, ES. (eds) Neural Information Processing. ICONIP 2017. Lecture Notes in Computer Science(), vol 10637. Springer, Cham. https://doi.org/10.1007/978-3-319-70093-9_58
Download citation
DOI: https://doi.org/10.1007/978-3-319-70093-9_58
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70092-2
Online ISBN: 978-3-319-70093-9
eBook Packages: Computer ScienceComputer Science (R0)