Insensibility of the Second Order Sliding Mode Control via Measurement Noises: Application to a Robot Manipulator Surveillance Camera | SpringerLink
Skip to main content
Springer Nature Link
Log in

Insensibility of the Second Order Sliding Mode Control via Measurement Noises: Application to a Robot Manipulator Surveillance Camera

  • Chapter
  • First Online:
Applications of Sliding Mode Control in Science and Engineering

Part of the book series: Studies in Computational Intelligence ((SCI,volume 709))

Abstract

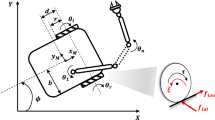
The Sliding Mode Control (SMC) is a widely spread approach thanks to its efficiency and robustness. However, it suffers from the undesirable chattering phenomenon which leads to the mechanical system damage. Then, this study takes into consideration the second order SMC which is known by its reliability regarding disturbances and nonlinear uncertainties, in order to improve the system stability and performances. In fact, such a high order SMC ensures a trade off between chattering reduction and disruption resistance. First, a second order sliding mode controller has been elaborated. Then, and in order to test the robustness of the proposed strategy, a measurement noise has been introduced. Simulation results show the efficiency of the proposed second order SMC applied to a robot manipulator system in a motion control task, which is used to ensure the displacement of a surveillance camera.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 11439
Price includes VAT (Japan)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 14299
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
JPY 14299
Price includes VAT (Japan)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen M, Chen WH (2010) Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int J Adapt Control Signal Process 24:51–64

    MathSciNet  MATH  Google Scholar 

  2. Sira-Ramirez H (1992) On the sliding mode control of nonlinear systems. Syst Control Lett 19:303–312

    Article  MathSciNet  MATH  Google Scholar 

  3. Gao W, Wang Y, Homaifa A (1995) Discrete-time variable structure control systems. IEEE Trans Ind Electron 42:117–122

    Article  Google Scholar 

  4. Shtessel Y, Edwards C, Fridman L, Levant A (2014) Introduction: intuitive theory of sliding mode control. In: Sliding mode control and observation. Springer, New York, pp 1–42

    Google Scholar 

  5. Vaidyanathan S, Azar AT (2015) Hybrid synchronization of identical chaotic systems using sliding mode control and an application to Vaidyanathan chaotic systems. Stud Comput Intell 576:549–569

    Google Scholar 

  6. Piltan F, Sulaiman N, Marhaban MH (2011) Design of FPGA based sliding mode controller for robot manipulator. Int J Robot Autom 2:183–204

    Google Scholar 

  7. Xu L, Yao B (2001) Adaptative robust precision motion control of linear motors with negligible electrical dynamics: theory and experiments. IEEE Trans Mechatron 6:444–452

    Article  Google Scholar 

  8. Shafiei SE (2010) Sliding mode control of robot manipulators via intelligent approaches. INTECH Open Access Publisher

    Google Scholar 

  9. Perruquetti W, Barbot JP (2002) Sliding mode control in engineering. CRC Press Publisher

    Google Scholar 

  10. Levant A (2010) Chattering analysis. IEEE Trans Autom Control 55:1380–1389

    Article  MathSciNet  Google Scholar 

  11. Vaidyanathan S (2016) Anti-synchronization of 3-cells cellular neural network attractors via integral sliding mode control. Int J PharmTech Res 9:193–205

    Google Scholar 

  12. Kapoor N, Ohri J (2013) Integrating a few actions for chattering reduction and error convergence in sliding mode controller in robotic manipulator. Int J Eng Res Technol 2

    Google Scholar 

  13. Vaidyanathan S (2015) Global chaos synchronization of 3-cells cellular neural network attractors via integral sliding mode control. Int J PharmTech Res 8:118–130

    Google Scholar 

  14. Vaidyanathan S (2015) Global chaos control of 3-cells cellular neural network attractor via integral sliding mode control. Int J PharmTech Res 8:211–221

    Google Scholar 

  15. Golea N, Debbache G, Golea A (2012) Neural network-based adaptive sliding mode control for uncertain non-linear mimo systems. Int J Model Ident Control 16:334–344

    Article  Google Scholar 

  16. Kapoor N, Ohri J (2013a) Fuzzy sliding mode controller (FSMC) with global stabilization and saturation function for tracking control of a robotic manipulator. J Control Syst Eng 1:50

    Article  Google Scholar 

  17. Slotine JJE, Li W (1991) Applied nonlinear control. Prentice Hall, Englewood Cliffs, NJ

    Google Scholar 

  18. Zinober ASI, ElGhezawi OE, Billings SA (1982) Multivariable structure adaptive model following control systems. IEE Proc D (Control Theor Appl) IET Digital Libr 129:6–12

    Google Scholar 

  19. Vaidyanathan S (2016) Global chaos regulation of a symmetric nonlinear gyro system via integral sliding mode control. Int J ChemTech Res 9:462–469

    Google Scholar 

  20. Fridman L, Levant A (2002) Higher order sliding modes. Sliding Mode Control Eng 11:53–102

    Google Scholar 

  21. Vaidyanathan S (2016) A highly chaotic system with four quadratic nonlinearities, its analysis, control and synchronization via integral sliding mode control. Int J Control Theory Appl 9:279–297

    Google Scholar 

  22. Vaidyanathan S, Sampath S (2016) A novel hyperchaotic system with two quadratic nonlinearities, its analysis and synchronization via integral sliding mode control. Int J Control Theory Appl 9:221–235

    Google Scholar 

  23. Bartolini G, Pydynowski P (1996) An improved, chattering free, VSC scheme for uncertain dynamical systems. IEEE Trans Autom Control 41:1220–1226

    Article  MATH  Google Scholar 

  24. Bartolini G, Ferrara A, Usani E (1998) Chattering avoidance by second-order sliding mode control. IEEE Trans Autom Control 43(2):241–246

    Google Scholar 

  25. Ferrara A, Magnani L (2007) Motion control of rigid robot manipulators via first and second order sliding modes. J Intell Robot Syst 48:23–36

    Article  Google Scholar 

  26. Abdelhedi F, Bouteraa Y, Derbel N (2014) Distributed second order sliding mode control for synchronization of robot manipulator. In: Second international conference on automation, control, engineering and computer science

    Google Scholar 

  27. Vaidyanathan S, Sampath S (2016) Hybrid synchronization of identical chaotic systems via novel sliding control method with application to Sampath four-scroll chaotic system. Int J Control Theory Appl 9:321–337

    Google Scholar 

  28. Vaidyanathan S, Sampath S (2016) Anti-synchronization of identical chaotic systems via novel sliding control method with application to Vaidyanathan-Madhavan chaotic system. Int J Control Theory Appl 9:85–100

    Google Scholar 

  29. Vaidyanathan S, Sampath S, Azar AT (2015) Global chaos synchronisation of identical chaotic systems via novel sliding mode control method and its application to Zhu system. Int J Model Ident Control 23:92–100

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Control & Energy Management Laboratory (Cemlab), Sfax Engineering School, University of Sfax, Sfax, Tunisia

    Marwa Fathallah & Fatma Abdelhedi

  2. Sfax Engineering School, University of Sfax, Sfax, Tunisia

    Nabil Derbel

Authors
  1. Marwa Fathallah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fatma Abdelhedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nabil Derbel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marwa Fathallah .

Editor information

Editors and Affiliations

  1. Research and Development Centre, Vel Tech University, Chennai, Tamil Nadu, India

    Sundarapandian Vaidyanathan

  2. Maritime College and Department of Marine Engineering, National Kaohsiung Marine University, Kaohsiung, Taiwan

    Chang-Hua Lien

Rights and permissions

Reprints and permissions

Copyright information

© 2017 Springer International Publishing AG

About this chapter

Cite this chapter

Fathallah, M., Abdelhedi, F., Derbel, N. (2017). Insensibility of the Second Order Sliding Mode Control via Measurement Noises: Application to a Robot Manipulator Surveillance Camera. In: Vaidyanathan, S., Lien, CH. (eds) Applications of Sliding Mode Control in Science and Engineering. Studies in Computational Intelligence, vol 709. Springer, Cham. https://doi.org/10.1007/978-3-319-55598-0_5

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-55598-0_5

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-55597-3

  • Online ISBN: 978-3-319-55598-0

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics

Search

Navigation