Abstract
A critical aspect of rational belief revision that has been neglected by the classical AGM framework is what we call the principle of kinetic consistency. Loosely speaking, this principle dictates that the revision policies employed by a rational agent at different belief sets, are not independent, but ought to be related in a certain way. We formalise kinetic consistency axiomatically and semantically, and we establish a representation result explicitly connecting the two. We then combine the postulates for kinetic consistency, with Parikh’s postulate for relevant change, and add them to the classical AGM postulates for revision; we call this augmented set the extended AGM postulates. We prove the consistency and demonstrate the scope of the extended AGM postulates by showing that a whole new class of concrete revision operators introduced hererin, called PD operators, satisfies all extended AGM postulates. PD operators are of interest in their own right as they are natural generalisations of Dalal’s revision operator. We conclude the paper with some examples illustrating the strength of the extended AGM postulates, even for iterated revision scenarios.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
- 2.
To be precise, Katsuno and Mendelzon represent an agent’s beliefs by a sentence rather than a theory. Hence they assign preorders to sentences rather than to theories. We use theories in order to adhere more closely to the original AGM approach. Since we deal only with languages built over finitely many variables, the difference is immaterial.
- 3.
A partition \(Q'\) refines another partition Q, iff for every \(Q'_i \in Q'\) there is \(Q_j \in Q\), such that \(Q'_i \subseteq Q_j\).
- 4.
Since
 is a total preorder and \([K]\) is finite (because P is assumed to be finite), such a minimal element always exists.
is a total preorder and \([K]\) is finite (because P is assumed to be finite), such a minimal element always exists. - 5.
To see that such a world indeed exists, consider the sentence \(\varphi \) defined as the conjunction of all literals in \(r\) that are built from variables in \(P-{{ Diff}}( K,r )\). Clearly then, \(r\,\models \, \psi \). Moreover, \(\lnot \psi \not \in K\), for otherwise \({{ Diff}}( K,r )\) would include variables from \(P-{{ Diff}}( K,r )\), which is of course a contradiction. Hence there is a \(u\in [K]\) such that \(u\,\models \, \psi \). By the construction of \(\psi \) it follows that \(u\) agrees with \(r\) on all variables outside \({{ Diff}}( K,r )\).
References
Alchourron, C., Gardenfors, P., Makinson, D.: On the logic of theory change: partial meet functions for contraction and revision. J. Symbol. Logic 50, 510–530 (1985)
Dalal, M.: Investigations into theory of knowledge base revision: preliminary report. In: Proceedings of 7th National Conference of the American Association for Artificial Intelligence (AAAI 1988), pp. 475–479 (1988)
Darwiche, A., Pearl, J.: On the logic of iterated belief revision. Artif. Intell. 89, 1–29 (1997)
Grove, A.: Two modellings for theory change. J. Philos. Logic 17, 157–170 (1988)
Jin, Y., Thielscher, M.: Iterated belief revision, revised. Artif. Intell. 171, 1–18 (2007)
Katsuno, H., Mendelzon, A.: Propositional knowledge base revision and minimal change. Artif. Intell. 52(3), 263–294 (1991)
Konieczny, S., Perez, R.P.: A framework for iterated revision. J. Appl. Non-Classical Logics 10, 339–367 (2000)
Nayak, A., Pagnucco, M., Peppas, P.: Dynamic belief revision operators. Artif. Intell. 146, 193–228 (2003)
Parikh, R.: Beliefs, belief revision, and splitting languages. In: Logic, Language, and Computation - CSLI Lecture Notes, vol. 2, pp. 266–278. CSLI Publications (1999)
Peppas, P.: Belief revision. In: van Harmelen, F., Lifschitz, V., Porter, B. (eds.) Handbook of Knowledge Representation, pp. 317–359. Elsevier Science (2008)
Peppas, P., Williams, M.-A., Chopra, S., Foo, N.: Relevance in belief revision. Artif. Intell. 229, 126–138 (2015)
Peppas, P.: A panorama of iterated revision. In: Ove Hansson, S. (ed.) David Makinson on Classical Methods for Non-Classical Problems. Outstanding Contributions to Logic, pp. 71–94. Springer, Netherlands (2014)
Acknowledgements
We are grateful to Fanis Aravanis and to the anonymous reviewers for valuable comments on this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Peppas, P., Williams, MA. (2016). Kinetic Consistency and Relevance in Belief Revision. In: Michael, L., Kakas, A. (eds) Logics in Artificial Intelligence. JELIA 2016. Lecture Notes in Computer Science(), vol 10021. Springer, Cham. https://doi.org/10.1007/978-3-319-48758-8_26
Download citation
DOI: https://doi.org/10.1007/978-3-319-48758-8_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48757-1
Online ISBN: 978-3-319-48758-8
eBook Packages: Computer ScienceComputer Science (R0)



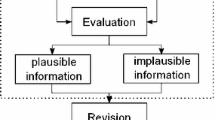
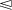 is a total preorder and
is a total preorder and