Authenticated Key Agreement Mediated by a Proxy Re-encryptor for the Internet of Things

Abstract

The Internet of Things (IoT) is composed of a wide range of heterogeneous network devices that communicate with their users and the surrounding devices. The secure communications between these devices are still essential even with little or no previous knowledge about each other and regardless of their resource capabilities. This particular context requires appropriate security mechanisms which should be well-suited for the heterogeneous nature of IoT devices, without pre-sharing a secret key for each secure connection.

In this work, we first propose a novel symmetric cipher proxy re-encryption scheme. Such a primitive allows a user to delegate her decryption rights to another with the help of a semi-trusted proxy, but without giving this latter any information on the transmitted messages and the user’s secret keys. We then propose AKAPR, an Authenticated Key Agreement mediated by a Proxy Re-encryptor for IoT. The mechanism permits any two highly resource-constrained devices to establish a secure communication with no prior trust relationship. AKAPR is built upon our proposed proxy re-encryption scheme. It has been proved by ProVerif to provide mutual authentication for participants while preserving the secrecy of the generated session key. In addition, the scheme benefits from the lightness of our proxy re-encryption algorithm as it requires no expensive cryptographic operations such as pairing or modular exponentiation.

1 Introduction

The Internet of Things (IoT) paradigm implies a network of heterogeneous devices (things) that evolves constantly in terms of complexity and scale. According to Garner’s forecast [1], the number of active wireless devices will exceed 25 billions of units by 2020. More connected devices mean more attack vectors and more difficulties to protect these devices. In addition, IoT security issues concern not only civil applications (e.g. monitoring live home temperature and humidity) but also critical applications, for instance, the Internet-connected cars or the remote patient monitoring in healthcare. These applications can be compromised when secure channels are not properly implemented. Hence, secure communications between IoT devices become no longer an option, but a requirement.

Due to limited resources and highly interconnected objects, there is a strong need to design lightweight and scalable key establishment protocols. The existing solutions that require the pre-distribution of secret keys cannot be envisioned. Indeed, we cannot pre-share every time a common secret key in each device because the number of connected devices composing the network is very important. If the key pre-distribution is not considered, most of the existing schemes require expensive cryptographic operations to establish a session key between entities that do not share common credentials a priori such as ECDH-based approaches [26]. Indeed, Sciancalepore et al. [26] propose a key agreement protocol with implicit certificates in the context of IoT. Their approach requires four costly operations in order to negotiate a common key between two parties. In addition, the negotiation algorithm always produces the same key for a given couple of devices, which can be vulnerable to known-key attacks. Many other efforts (e.g. in [23, 24]) have been undertaken to reduce the overhead of standard security protocols so that they can fit in low power computing sensor platforms. However, these solutions still require the executions of costly cryptographic operations on such platforms.

The aforementioned heavyweight computations can be handled by a resource-rich server. Server-assisted approaches for key establishment protocols have been proposed in this respect for IoT. As such, Fouladgar et al. [17] introduce an adaption and an extension of TLS (Transport Layer Security) handshake to the Wireless Sensor Network. Their solution describes an ECDH key establishment between a constrained sensor node and an external entity mediated by a partially trusted gateway. Such solution requires only two costly operations on the constrained node side. However, the gateway is able to launch a man-in-the-middle attack and to establish a common Diffie-Hellman key with each party without anyone noticing. Saied et al. [25] propose a lightweight collaborative key agreement based on Diffie-Hellman (DH) key establishment. Their idea is to delegate the heavyweight cryptographic calculation of DH values to the resource-unconstrained trusted proxies in neighborhood. Such mechanism requires a sufficient number of non-colluding neighbors in proximity. Besides, it may seem unpractical, since the two end nodes, which do not share any relation, may not be in possession of a secure established link with those common proxies. Several works attempt to build a common secret key for any two entities using the DTLS (Datagram TLS) protocol in the context of IoT. Their approach is to delegate partially [18, 29] or totally the DTLS handshake [20] to a third party. Such mechanism removes the overhead of intensive calculations for the constrained-devices. However, the third party can read all communications between sensor nodes and the Internet hosts. This feature is not desirable in certain scenarios especially when we do not trust the server. We remove such inconvenience by applying a lightweight proxy re-encryption mechanism in our proposed key establishment mechanism.

Lighter proxy re-encryption schemes can help to design scalable key establishment mechanisms. The proxy can translate a ciphertext encrypted under one key to another but is not allowed to learn anything on either keys. There exists many PRE schemes in the literature (e.g. in [2, 7, 19, 22]). Their applications are diverse such as encrypted mail forwarding system, secure data storage on semi-trusted servers. In this paper, we present an application of PRE to build a server-assisted key agreement protocol where the server is unable to recover not only the secret keys of communicating parties but also the negotiated session keys.

Our contribution: In this work, we first propose a lightweight proxy re-encryption that uses a symmetric cipher to encrypt data. Our scheme is able to convert a ciphertext from one key to another without placing trust entirely on the proxy and without computing heavyweight computational operations. Second, based on the proposed re-encryption scheme, we build an efficient authenticated key agreement mediated by a proxy re-encryptor, namely AKAPR, for IoT services. The scheme allows us to establish common secret keys between devices, even highly resource-constrained ones (e.g. class 1 devices [9]). Third, we present a formal security validation of AKAPR using ProVerif [6]. The results show that AKAPR provides mutual authentication for participants and ensures the secrecy of the generated session keys.

Paper outline: The rest of this paper is organized as follows. Section 2 provides several notations and recalls cryptographic definitions of a proxy re-encryption scheme. We present a novel lightweight proxy re-encryption construction in Sect. 3. Section 4 describes in detail our proposed authenticated key agreement AKAPR for IoT. Section 5 provides an informal security analysis of AKAPR against common attacks with a formal security validation done by the cryptographic verifier ProVerif [6]. Finally, the conclusion remarks are given in Sect. 6.

2 Preliminaries

2.1 Notations and Abbreviation

The definitions and terms used throughout the rest of this paper are presented in Table 1.

Table 1. Abbreviations

Definition 1

(Symmetric cipher proxy re-encryption). A symmetric cipher proxy re-encryption consists of five algorithms ($\mathsf {KeyGen}, \mathsf {ReKeyGen}, \mathsf {Encrypt}$, $\mathsf {Decrypt}, \mathsf {Reencrypt}$) with the following functionalities:

• $\mathsf {KeyGen}(k) \rightarrow (id_A, id_B, sk_A, sk_B)$. Given a security level parameter k, output the identifiers and the secret keys for two entities A and B. These keys are to be used in the encryption and decryption processes.

• $\mathsf {ReKeyGen}(id_A, id_B, sk_A, sk_B) \rightarrow rk_{A \rightarrow B}$. Given the identifiers and secret keys of A and B, output the re-encryption key $rk_{A \rightarrow B}$.

• $\mathsf {Encrypt}(id_A, sk_A, M, id_B) \rightarrow C_A$. Given the identifiers ($id_A, id_B$), the secret key $sk_A$ and a message M, return the ciphertext $C_A$.

• $\mathsf {Reencrypt}(rk_{A \rightarrow B}, C_A) \rightarrow C_B$. Given a ciphertext $C_A$ encrypted by the entity A and the re-encryption key $rk_{A \rightarrow B}$, return a ciphertext $C_B$ to be decrypted by B.

• $\mathsf {Decrypt}(id_B, sk_B, C_B, id_A) \rightarrow M$. Given a secret $sk_B$ and a ciphertext $C_B$ and the identifiers ($id_A, id_B$), return the plaintext M.

3 The Basic Idea: Lightweight Bi-directional Proxy Re-encryption Scheme with Symmetric Cipher

In this section, we first specify general definitions and the most useful properties of a PRE scheme. We present subsequently several related PRE propositions in the literature. Then, the concrete description of our proposed symmetric cipher PRE scheme is given which is followed by a comparison with related solutions in terms of supported properties and performance.

3.1 Properties of a Proxy Re-encryption Scheme

In a proxy re-encryption scheme, Alice can delegate the decryption right on an encryption to Bob with the help of a semi-trusted proxy (i.e. An entity that acts and returns correct results according to demanded tasks but can be untrusted when processing sensitive data). In general, the proxy uses a prior provided secret, namely, proxy key or re-encryption key, to translate a ciphertext dedicated to Alice to another one dedicated to Bob. However, it cannot gain any information on the secret keys of Alice or Bob and is unable to read the content of the encrypted messages.

Proxy re-encryption schemes are characterized according to different criteria. The works in [19] and [7] provide several properties by which to compare different proxy re-encryption schemes. We briefly redefine these desirable properties as follows.

• Uni-directionality: The proxy re-encryption scheme is said to be unidirectional if the re-encryption key of the proxy can be used in only one direction. In contrast, a bidirectional proxy re-encryption scheme permits the re-encryption key to be used to translate encrypted messages from Alice to Bob and vice versa.

• Non-Interactivity: In a non-interactive scheme, Alice can generate a re-encryption key, while offline, from its secret key and Bob’s public values without the participation of the Key Distribution Center (KDC), the proxy, or Bob. On the other hand, interactive schemes require the participation of parties (including KDC) to generate the re-encryption keys.

• Multiple-use: Some proxy re-encryption schemes can re-encrypt a ciphertext multiple times. For example, Bob can demand a re-encryption of a ciphertext re-encrypted for him which is previously intended to Alice to obtain a ciphertext dedicated to Charlie without actually decrypting the message. Such scheme is called mutiple-use. In opposition, a single-use proxy re-encryption scheme permits the proxy to perform only one re-encryption on a ciphertext.

• Non-transitivity: In a non-transitive scheme, the proxy cannot combine provided re-encryption keys to re-delegate decryption rights. For example, given three entities A, B and C, the proxy is unable to construct the re-encryption key $rk_{A \rightarrow C}$ from A to C from the two supplied re-encryption keys $rk_{A \rightarrow B}$ and $rk_{B \rightarrow C}$.

• Collusion resistance: In a proxy re-encryption scheme, it is desirable that Bob even colluding with the proxy, can not guess the secret key of Alice.

Table 2. Two existing approaches of a proxy re-encryption scheme

3.2 Existing Approaches on Proxy Re-encryption

Blaze et al. [7] first proposed the notion of proxy cryptography where Alice (A) can securely delegate her decryption rights or her digital signatures to another party Bob (B) with the help of a proxy. Many works on proxy re-encryption schemes have been proposed in the literature. We classify these schemes into two categories as depicted in Table 2: (a) Proxy re-encryption schemes that employ asymmetric ciphers (public key cryptography) to encrypt the message and (b) Proxy re-encryption schemes that employ symmetric ciphers to encrypt the message. Most of the proposed schemes use a public key primitive to encrypt the message. In [7], the authors propose the very first proxy re-encryption scheme based on Elgamal cryptosystem [15]. Alice first generates the ciphertext $C_A = (m.g^r, g^{ar})$ on message m using its pair of public/private key ($sk_A = a, \, pk_A = g^a$). The proxy uses subsequently the re-encryption key $rk_{A \rightarrow B} = b/a$ to obtain $g^{br} = (g^{ar})^{rk_{A \rightarrow B}}$. Hence, B receives the new ciphertext $C_B = (m.g^r, g^{br})$ encrypted under his secret key. This scheme is bidirectional, transitive and exposed to collusion attacks. As such, the proxy can compute $(rk_{A \rightarrow B})^{-1}$ to obtain the re-encryption key in the opposite direction from B to A. In addition, the proxy can combine the two re-encryption keys $rk_{A \rightarrow B}$ and $rk_{B \rightarrow C}$ to get the valid re-encryption key from A to C ($rk_{A \rightarrow C} = a/c = (a/b)\,.\,(b/c)$). Such property is sometimes unwanted. Furthermore, if the proxy colludes with one party, it is trivial for them both to learn the secret key of the other party. Ateniese et al. [2] proposed an unidirectional pairing-based proxy re-encryption scheme that fixes the above issues. They use a proxy key in the form of $rk_{A \rightarrow B} = g^{a/b}$. Such configuration provides non-transitivity and collusion-resistance properties. Indeed, the possession of ($rk_{A \rightarrow B} = g^{a/b}, rk_{B \rightarrow C} = g^{b/c}$) does not permit the proxy to find out $rk_{A \rightarrow C} = g^{a/c}$ due to the Decisional Diffie-Hellman Problem [8]. In addition, colluding with Bob does not help the proxy to discover the secret key of Alice and vice versa since having $g^{a/b}$ and b does not help him to recover a due to the Discrete Logarithm Problem. From then onwards, many schemes based on pairing operations have been proposed including Identity-based (IBE) proxy re-encryption schemes [19, 22]. They are proved to be secure under chosen ciphertext attack (CCA) assumption. Pairing-free proxy re-encryption schemes exist, for example [11, 12], but multiple modular exponentiations are still required.

There are several propositions on proxy re-encryption that employ symmetric ciphers to encrypt the message such as [13, 27]. The main advantage of symmetric cipher proxy re-encryption approach is the lightness of the employed symmetric cryptographic operations in terms of complexity and memory usage. In [13], Cook et al. propose two conversion functions for symmetric ciphers. In their first attempt, they assume that Alice shares with Bob a secret key $k_{ab}$. In addition, Alice and the proxy must share $k_a$. Then, Alice sends $E_{k_a}(E_{k_{ab}}(M))$ to the proxy. The proxy decrypts the obtained ciphertext with $k_a$ and sends the result $E_{k_{ab}}(M)$ to Bob. Hence, Bob does not need to share a key with the proxy and yet he can still get the message M. However, this assumes Alice and Bob must always share a common secret. Such assumption is not trivial when there exists a significant number of devices in the network, such as in the context of IoT. In their second attempt (termed as CK to be used in Table 3), the authors provide the proxy the key $k_p = k_a \oplus k_b$, built from the secret keys ($k_a, k_b$) of A and B, respectively. A computes $C = M \oplus k_a$ and sends it to the proxy. The proxy performs the conversion by computing $C' = k_p \oplus C = k_b \oplus M$. B can then decrypts $C'$ to get the message using its secret key $k_b$. This approach is efficient but not secure. Indeed, B can easily retrieve the secret key of A by computing $k_b \oplus C \oplus C' = k_a$. In [27], Syalim et al. propose a pure symmetric cipher proxy re-encryption algorithm. However, this approach requires that A and B share common secret keys a priori. Moreover, it is assumed that the proxy cannot collude with any previous users since a compromised user can recover the current encryption key if he/she has the re-encryption key.

3.3 Our Proposed Lightweight Proxy Re-encryption

In this section, we present in detail our proposed symmetric cipher proxy re-encryption. A symmetric cipher proxy re-encryption consists of five algorithms ($\mathsf {KeyGen}, \mathsf {ReKeyGen}, \mathsf {Encrypt}$, $\mathsf {Decrypt}, \mathsf {Reencrypt}$). In addition, we define $(\mathsf {Enc}, \mathsf {Dec})$ as the encryption and decryption algorithms of a symmetric encryption scheme. A key distribution center (KDC) is responsible for providing keying material. As such, KDC runs the two algorithms $\mathsf {KeyGen}$ and $\mathsf {ReKeyGen}$ to generate the needed security parameters. We suppose that Alice (A) desires to delegate the decryption right of a ciphertext $C_A$ encrypted under her secret key to Bob (B) with the help of the proxy (PR). Figure 1 describes the message exchanges of our proposed PRE scheme. The procedure is detailed as follows.

Fig. 1.

Our proposed symmetric cipher proxy re-encryption scheme

• $\mathsf {KeyGen}(k) \rightarrow (id_A, id_B, sk_A, sk_B)$: Given the security parameter k, this algorithm outputs the identifiers ($id_A, id_B$) and the secret keys ($sk_A, sk_B$) for A and B, respectively.

• $\mathsf {ReKeyGen}(id_A, sk_A, id_B, sk_B) \rightarrow rk_{A \rightarrow B}$: Given the identifiers and the secret keys of A and B, this algorithm returns the re-encryption key $rk_{A \rightarrow B} = (h(sk_A||id_B).h(sk_B||id_A))^{-1}$, where $h: {\{0, 1\}}^* \rightarrow \mathbb {Z}_p$ is a hash function that converts a string to a number on $\mathbb {Z}_p$. As we shall see, our construction results in the fact that $rk_{A \rightarrow B} = rk_{B \rightarrow A}$. This property makes our proxy-encryption scheme bidirectional meaning that the proxy only needs to store one re-encryption key to re-encrypt messages from A to B and vice versa.

• $\mathsf {Encrypt}(id_A, sk_A, M, id_B) \rightarrow C_A$: Given the identifier of B and a message M, A uses its identifier $id_A$ and its secret key $sk_A$ to generate a ciphertext $C_A$. A first chooses a random number $t \leftarrow \mathbb {Z}_p$. Then, it generates a symmetric key $K_t \leftarrow KDF(t)$, where KDF is a Key Derivation Function. Finally, it outputs the ciphertext $C_A = (\mathsf {Enc}_{K_t}(M), t.h(sk_A||id_B))$.

• $\mathsf {Reencrypt}(rk_{A \rightarrow B}, C_A) \rightarrow C_B$: Upon receiving the ciphertext $C_A = (C_1, C_2)$, PR keeps $C_1$ unchanged while multiplying $C_2$ with the re-encryption key $rk_{A \rightarrow B}$ to obtain the new ciphertext $C_B$ = $(\mathsf {Enc}_{K_t}(M)$, $t.h(sk_B||id_A)^{-1})$.

• $\mathsf {Decrypt}(id_B, sk_B, C_B, id_A) \rightarrow M$: Upon receiving $C_B = (C_1', C_2')$ $= (\mathsf {Enc}_{K_t}(M)$, $t.h(sk_B||id_A)^{-1})$, B first calculates the value of $l = h(sk_B||id_A)$ from its secret key and the identifier of A. Then, it obtains the value of t by multiplying l to $C_2'$. From t, B generates the symmetric key $K_t \leftarrow KDF(t)$. Then, it gets the message M by decrypting $C_1'$ using the generated key $K_t$: $M = \mathsf {Dec}_{K_t}(\mathsf {Enc}_{K_t}(M))$.

Correctness. The correctness of our proposed scheme is straightforward.

3.4 Comparison of Our PRE Scheme to Related Work

In Table 3, we compare several proxy re-encryption schemes in related work with our scheme based on the properties provided in Sect. 3.1. In comparing with asymmetric cipher PRE schemes, our scheme is much lighter in terms of computational cost. Indeed, the proposed construction does not necessitate any pairing or exponentiation operation. On the other hand, while providing equivalent performance compared with symmetric cipher proxy re-encryption schemes, our scheme is more robust against attacks from compromised receiver, semi-honest proxy and their corporation. We argue that our scheme provides most of the desirable properties as described in the following.

Table 3. Comparison of our scheme and related work

First, our scheme is bidirectional since $rk_{A \rightarrow B} = rk_{B \rightarrow A}$. This can be an advantage in the considered scenario (e.g. IoT) where the proxy has to store only one proxy key for any pair of devices. Second, in our construction, only KDC can provide the re-encryption key because it is generated from the secret keys of participants. This property makes our scheme interactive. However, the scheme can be made partially non-interactive such that A and B can negotiate a new proxy re-encryption key even when KDC is offline. In fact, A may generate a new secret key $sk'_A$ and compute $k_1 = h(sk'_A||id_B).h(sk_A||id_B)$. B generates also a new secret key $sk'_B$ and compute $k_2 = h(sk'_B||id_A).h(sk_B||id_A)$. $k_1, k_2$ are then sent to the proxy. The latter can now obtain the new proxy re-encryption key by computing $1/(k_1.k_2.rk_{A \rightarrow B})$ in $\mathbb {Z}_p$. Finally, as each proxy key is generated specifically for a pair of users, the proxy can only re-encrypt the ciphertext a single time. Such construction makes our scheme unconditionally non-transitive and collusion-resistant. Indeed, providing $rk_{A \rightarrow B} = (h(sk_A||id_B).h(sk_B||id_A))^{-1}$ and $rk_{B \rightarrow C} = (h(sk_B||id_C).h(sk_C||id_B))^{-1}$, the only way that the proxy can get $rk_{A \rightarrow C}$ is to have the secret keys of A and C due to one-way property of hash function. Even if B colludes with the proxy, they only have the value of $h(sk_A||id_B)$ which is only used in the communication between A and B. Such knowledge will not help them to find out A’s secret key $sk_A$. In addition, to obtain $rk_{A \rightarrow C}$, they still need both the secret keys of A and C.

4 Lightweight Authenticated and Mediated Key Agreement for IoT

In this section, we present the application of our PRE scheme presented in Sect. 3.3 to obtain a very lightweight key establishment mechanism. Our protocol is relevant even with highly resource-constrained devices in the context of IoT. The first subsection presents the network architecture and our considered scenarios. The second subsection provides the security assumptions needed for the description of the protocol. Then, we describe concretely the message exchanges of our proposal.

4.1 Network Architecture and Scenario Description

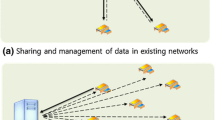
Figure 2 describes the network architecture of our proposal. The considered network of things consists of a number of tiny nodes communicating with each other and with an unconstrained resource border router (or gateway). The gateway is the bridge between the sensor network and the outside world. It may take part in the communication between two entities in a passive (transparent to the communicating parties) or active (as a mediator in the communication process) manners.

Our key establishment protocol involves the four following actors:

• Two parties: an Initiator (I) and a Responder (R), which respectively initiates the communication and responds to incoming requests.

• A partial trusted party, named as Delegatee (DG), which is responsible for assisting the key establishment process between I and R. In fact, DG is provided with a re-encryption key that allows it to translate the ciphertext from I to R. In addition, it is considered as a semi-trusted party that acts and returns correct results according to the protocol but can be curious on transmitted messages.

• A trusted Key Distribution Center (KDC), which is responsible for generating keying material and acts as the root of trust of the whole system. Besides, KDC is also in charge of delegation credential management and distribution.

Fig. 2.

Network architecture and considered scenarios (: KDC provides keying material for all actors in the system. Examples of scenario: (1) : The external user $I_1$ initiates a key agreement process (mediated by DG) with the resource-constrained sensor node $R_1$; (2) : Two unknown resource-constrained nodes ($I_2$ and $R_2$) initiate a key agreement process with the help of DG and then GW.)

In our considered scenario, I and R can be both resource-constrained devices. At the beginning, KDC provisions the keying material for all users on the system. Hence it can stay offline until the security parameters need to be refreshed. On the other hand, DG must stay online and participate actively in the key establishment procedure. Our motivation is that DG acts as a partially-trusted third party helping the constrained devices to negotiate session keys without obtaining any knowledge about these keys.

As depicted in Fig. 2, the initiator can be an external entity requesting for information of the Responder - a sensor platform device lying in a Wireless Sensor Networks (WSN). The key negotiation process is assisted by DG. In addition, when I and R are in the same WSN, DG can provide the delegation keys for the border router (or gateway) so that the key agreement process can be done locally. Note that the gateway is also considered semi-trusted as a consequence of which it only knows the delegation keys and is not able to recover the secret keys of I and R. We provide more details on the security analysis of our proposal in Sect. 5.

4.2 Security Assumptions and Notations

We suppose that I and R possess their own secret keys ($sk_I$ and $sk_R$, accordingly). However, they do not have any common secrets a priori. On the other hand, DG shares with each communicating entity X a secret symmetric key $K_{xd}$ which is employed to protect the integrity of the traffic between X and DG. As a result, DG shares the secret keys $K_{id}$ and the secret key $K_{rd}$ with I and R, respectively. In addition, we use an incremental counter in both communicating parties to mitigate the replay attacks. For example, we maintain the counter $CT_{IR}$ in I’s side for all exchanges with R. If this is the first time that I communicates with R, $CT_{IR}$ is set to 0. It is increased by 1 after every successful key agreement. Furthermore, for each entity X, we denote its identifier as $id_X$. Such identifier must be unique for each entity. We also define $(\mathsf {Enc}, \mathsf {Dec})$ as the encryption and decryption algorithms of a symmetric encryption scheme. While, ($\mathsf {AEnc}, \mathsf {ADec}$) is an authenticated encryption algorithm such that $\mathsf {AEnc}_{K_1, K_2}(M) = \mathsf {Enc}_{K_1}(M)||MAC_{K_2}(\mathsf {Enc}_{K_1}(M))$ and $\mathsf {ADec}_{K_1, K_2}(\mathsf {Enc}_{K_1}(M)||MAC_{K_2}(\mathsf {Enc}_{K_1}(M))) = M$, for each message M and two secret keys $K_1, K_2$. Each key agreement exchange of order i between I and R (Message i, for $i = 1, 2, 3$) has two components $ED_i$ and $MAC_i(K)$. $ED_i$ defines the appended security parameters and the encrypted data, while $MAC_i(K)$ denotes the MAC of $ED_i$ computed with the symmetric key K.

In addition, two hash function $h: {\{0, 1\}}^* \rightarrow \mathbb {Z}_p$ and $H: {\{0, 1\}}^* \rightarrow {\{0, 1\}}^n$ are also defined, where n is an integer number generated from the input security level. These functions are modeled as random oracles [5]. Such oracle produces a random value for each new query. Of course, if an input is asked twice, identical answers are returned. In this work, we also use a Key Derivation Function (KDF) for generating a symmetric key. KDF is based on a solid pseudorandom number generator (PRNG) (e.g. in [3]). This function is initialized with several secret values, called seeds. An attacker with the knowledge of PRNG output should not be able to guess the seeds other than by exhaustive guessing.

4.3 AKAPR Message Sequence Chart

The proposed key establishment protocol AKAPR consists of four messages as depicted in Fig. 3. The key negotiation process is mediated by DG. The detailed description of the key agreement process is given as follows.

Message 1 from I to DG: To start a new session, I first increases $CT_{IR}$ by one, where $CT_{IR}$ denotes the current counter of I for all communications with R. $CT_{IR}$ is set to zero if this is the first time I communicates with R. Next, it generates a session identifier SID at random (e.g. $SID = H(id_I||id_R||w)$, where w is randomly chosen in $\mathbb {Z}_p$). Then, I chooses at random two fresh numbers $N_i$ and t from $\mathbb {Z}_p$. The ephemeral authentication keys $AK = (AK_e, AK_a)$ are then generated from $id_I, id_R$ and t using a key derivation function (KDF). To construct the Message 1, I concatenates the session identifier SID, its identifier $id_I$ and R’s identifier $id_R$ to ($N_i, CT_{IR}$). The concatenation is then encrypted using the algorithm $\mathsf {AEnc}$. As we shall see, the resulting ciphertext is the encryption and MAC of the concatenation by the pair of keys ($AK_e, AK_a$). This guarantees that the attacker (including DG) cannot modify the encrypted text of the concatenation. Second, I masks the value of t by multiplying it with the hashed value $h(sk_I ||id_R)$, where $sk_I$ is the secret key of I. As we shall see, the result of such multiplication is randomly distributed in $\mathbb {Z}_p$ since the two used operands are also randomly generated in $\mathbb {Z}_p$. Then, the first five components of the message $(SID, id_I, id_R, \mathsf {AEnc}_{AK_e, AK_a}(id_I||id_R||N_i||CT_{IR})$, $t.h(sk_I||id_I))$ is completed by a MAC computed with $K_{id}$, to form the Message 1.

Message 2 from DG to R: Upon receiving the Message 1 from I, DG first verifies that SID is fresh. We suppose that DG stores a list of SID values for each pair of I and R. Next, DG validates that the message has not been modified by an attacker by verifying its MAC using $K_{id}$. If the verification holds, DG is also certain that the Message 1 has not been replayed. Then, it modifies the fifth component of the encryption part ($ED_1$) in the Message 1 with the delegation key $dk_{IR}$. Indeed, it multiplies $t.h(sk_I||id_R)$ with $dk_{IR} = (h(sk_I||id_R).h(sk_R||id_I))^{-1}$ to obtain $t.h(sk_R||id_I)^{-1}$. DG now concatenates the obtained result to the first four components of the Message 1 to form $ED_2$. The encryption part of the Message 2, $ED_2 = (SID, id_I, id_R, \mathsf {AEnc}_{AK_e, AK_a}(id_I||id_R||N_i||CT_{IR})$, $t.h(sk_R||id_I)^{-1}$), is then appended with a MAC computed with $K_{rd}$.

Message 3 from R to I: When receiving the Message 2 from DG, R first verifies the authenticity of the message by employing its shared key with DG, $K_{rd}$. Then, by multiplying the hashed value of its secret key $sk_R$ and the identifier of I ($id_I$) to the fifth part of $ED_2$, ($t.h(sk_R||id_I)^{-1}$), it obtains t, which is a number on $\mathbb {Z}_p$. From t, I generates the secret ephemeral authentication keys $AK = KDF(id_I, id_R, t) = (AK_e, AK_a)$. Next, it decrypts the fourth part of the Message 2 using $(AK_e, AK_a)$ to get the value of ($id_I, id_R, N_{i1}, CT'$). It verifies subsequently that $CT'$ is superior or equal to its counter number $CT_{RI}$ to be sure about the freshness of the Message 2 (see Sect. 5.1). The counter value of R, $CT_{RI}$, is now set to the value of $CT'$. To construct the Message 3, R first chooses randomly $N_r$ from $\mathbb {Z}_p$. Next, it increases $CT_{RI}$ by one. R now encrypts the concatenation of ($SID, id_R, id_I, N_{i1}, t, N_r$) with the generated key $AK_{e}$. The encrypted data is then appended with the session identifier SID to obtain the encryption part. The latter is finally integrity protected with a MAC based on the generated secret key $AK_{a}$.

Message 4 from I to R: After receiving the Message 3 from R, I first approves the authenticity of the message using $AK_{a}$. Next, it decrypts the encrypted part by employing the secret key $AK_{e}$ to get the values of ($SID_1, id_R, id_I, N_{i2}, t_1$, $N_{r1}, CT_{RI1}$). I verifies that ($SID_1, N_{i2}, t_1$) is equal to the generated values ($SID, N_i, t$). It also verifies that $CT_{RI1} = CT_{IR} + 1$. Finally, the session keys are generated from the values ($CT_{RI1}$, $N_i$, $N_{r1}$) and the identifiers of I and R: $K_{s} = KDF(CT_{RI1}, id_I, id_R,N_i, N_{r1})$. I macs the concatenation of (SID, $id_I$, $id_R$, $N_i$, $N_{r1}$) using the session key $K_{s}$ and sends directly to R the hashed value appended with the session identifier SID as a key confirmation message.

Fig. 3.

Lightweight Secure Key Agreement for IoT (Meaning of abbreviations: $dk_{IR} = (h(sk_I||id_R).h(sk_R||id_I))^{-1}$; incr(CT): CT = $CT+1$; Message i = ($ED_i, MAC_i(K)$) for $i = 1, 2, 3$, e.g. $ED_1$ = ($id_I$, $id_R$, $\mathsf {AEnc}_{AK_e, AK_a}(id_I||id_R||N_i||CT_{IR}), t.h(sk_I||id_R))$, $MAC_1(K_{id})$ = $MAC_{K_{id}}(ED_1)$. Security keys needed for each participant: I ($CT_{IR}, sk_I, K_{id}$), DG ($K_{id}, K_{rd}, dk_{IR}$), R ($CT_{RI}, sk_R, K_{rd}$).)

Upon receiving the Message 4, R first generates the session key $K_{s}$ from the identifiers ($id_I, id_R$), the obtained $N_{i1}$ in the Message 2, the generated value $N_r$ and its counter number $CT_{RI}$. Then, it calculates a MAC from the concatenation of $(SID, id_I, id_R, N_{i1}, N_r)$ using the generated session key $K_{s}$. If the latter is identical to the received Message 4, I and R can now start secure communications, e.g. using standard security protocols such as DTLS-PSK [16] where the pre-shared keys are provided beforehand by our proposal.

5 Security Analysis

In this section, we first provide an informal security analysis of AKAPR by describing its resistance against common security attacks. Then, we validate the security of AKAPR using the cryptographic protocol analyzing tool ProVerif [6].

5.1 Resistance Against Attacks

Our proposal is resistant to the following attacks:

• Replay attack: This attack is mitigated by the used counter numbers ($CT_{IR}$, $CT_{RI}$) and the random numbers ($N_i, N_r$) at run-time. The replays of messages 1 and 2 are detected thanks to the counter numbers ($CT_{IR}, CT_{RI}$). Indeed, for any new session, I increases the value of $CT_{IR}$ by one. This value is then encrypted inside the Message 1. Upon receiving the Message 2, R can be sure about the freshness of this message by comparing its counter number $CT_{RI}$ with $CT'$. If the latter is inferior than $CT_{RI}$ then the message is detected as replayed. On the other hand, the freshness of the Messages 3 and 4 are assured by the pair of random values $N_r$ and $N_i$ since they are newly generated for each session. DG can also prevent replay attacks by keeping the session identifier SID. Because $CT_{IR}$ is increased by one for each communication, the latter will vary in each session.

• Denial-of-service attack (DoS): The Dos attacks aiming at each participant are reduced in our proposal because all exchanges between parties are authenticated. Indeed, each message is appended with an authentication code (MAC) that permits the receiving party to verify if the message is altered during the transmission. Further operations are canceled if the verification fails.

• Man in the middle attack (MITM): The attacker cannot impersonate any party in our protocol since each message is protected by the secret keys that are unknown to him. As such, the Message 1 and the Message 2 are encrypted-then-maced by $(AK_e, K_{id})$ and $(AK_e, K_{rd})$, respectively. The Message 3 is encrypted then maced by the ephemeral secret keys $AK = (AK_{e}, AK_{a})$, while, the Message 4 is protected by the new generated session key $K_{s}$.

• Key escrow attack: DG is a blind participant in the key agreement procedure. It aids the key negotiation without having any knowledge on the agreed session key and the secret keys of I and R. Indeed, although DG participates in the key negotiation process, it possesses only the delegation key $dk_{IR} = (h(sk_I||id_R).h(sk_R||id_I))^{-1}$) for each pair of Initiator and Responder. In addition, without knowing the secret key of I and R, DG cannot distinguish $dk_{IR}$, $t.h(sk_R||id_I)$ and $t.h(sk_I||id_R)^{-1}$ from a random number on $\mathbb {Z}_p$. The only actor that can intercept message exchanges between I, R and DG is the KDC. However, we have assumed that KDC is a totally trusted party which is responsible for the keying material generations and stays offline.

• Collusion attack: This feature inherits the collusion-resistance property of the proposed PRE scheme in Sect. 3. As such, even if DG colludes with one party, it cannot retrieve the secret key of the other party thanks to the one-way property of the hash function h. Indeed, if R collaborates with DG, they will get the values of $t, AK, N_i$ and $N_r$. However, only the messages dedicated for R of I are affected. In fact, DG can only have the value of $h(sk_I||id_R)$ which does not help him to find the secret key of I, $sk_I$. If DG colludes with I, I can then decrypt itself the Message 3, which contains no secret information of R. The colluding parties can achieve the value of $h(sk_R||id_I)$. However, they are unable to guess the secret $sk_R$ of R thanks again to the one-way property of hash functions.

The above security attacks except the MITM attacks, are usually impossible to be detected by an automatic software verifier (e.g. ProVerif [6]). In practice, the latter is used to verify if the essential security properties, such as mutual authentication and secret key protection, are provided in the testing cryptographic protocol. We provide more details on such software verification in the next section.

5.2 Formal Security Validation with ProVerif

In this section, we present a formal verification of AKAPR using ProVerif [6]. Our verification ensures that the proposed protocol provides the secrecy of the generated session keys and the authentication of participants.

ProVerif is an automatic verifier for cryptographic protocols defined in the Dolev-Yao model [14]. In such model, the attacker is an active eavesdropper, capable of obtaining any message passing in the network, initiating a conversation with any other users and impersonating as a legitimate receiver. It is only limited by the restrictions of the cryptographic methods used. In other words, the cryptographic primitives is considered idealized in the sense that they are unbreakable without knowing the employed secret keys.

In Listing 1.2, we provide the ProVerif verification code of our protocol AKAPR while respecting the description written in Sect. 4.3. A protocol description in ProVerif is divided into three parts: the declarations, the process macros and the main process. As described in Lines 1–44, the declaration part consists of the user types, the security properties, the cryptographic primitive functions and the list of defined events and queries. We define the types, the communication channel and the identifiers of the participating parties in Lines 1–6. The tables specified in Lines 8–11 are employed to model the storage of keys in a server. Only I, R and DG can use these tables to get the associations between host names and keys. Note that we use the table $\mathsf {ctr(host, Zp)}$ to store the counter value of a specific host. To describe the synchronization of the counter values in both sides (I and R), we model only the ideal situation where there is no failed session between them. In such case, the counter values of I and R are equal. The detailed synchronization process is described in Lines 52–54, 68, 87 and 90 of Listing 1.2. Furthermore, the secrecy assumptions are specified in Lines 13–16. For example, $\mathsf {sk\_I}$ and $\mathsf {K\_{id}}$ define the secret key of I and its shared key with DG. These keys are kept secret to the attackers. Then, Lines 18–30 describe the cryptographic functions needed in our protocol. For example, the function ($\mathsf {kdf\_h(Zp, host): Zp}$) generates the hashed value $\mathsf {h(aZpNumber||aHostName)}$. On the other hand, the function ($\mathsf {mask(Zp, Zp): Zp}$) denotes a simple multiplication on $\mathbb {Z}_p$. Other functions are self-explained according to the protocol specification as depicted in Sect. 4. As we shall see, the correctness of the re-encryption process is modeled in Lines 32–35 based on the commutativity of multiplication on $\mathbb {Z}_p$. Finally, we introduce a list of events and queries in Lines 37–44. For example, the event $\mathsf {beginRkey(host, host, key)}$ represents the request from I to create a trusted session with R. The defined events play as reference points for the protocol execution order.

In ProVerif, we can ensure the authentication by testing the correspondence assertions between the aforementioned events. Indeed, we verify the mutual authentication between I and R using queries defined in Lines 43–44. For example, the first query in Line 43 says that, if event $\mathsf {endRkey(host, host, key)}$ occurs then, event $\mathsf {beginRkey(host, host, key)}$ must have occurred before. Furthermore, our second interest of this protocol modeling is to verify the secrecy of the negotiated session key $\mathsf {K\_s}$. To do so, I and R choose a random number in each side and output the ciphertext encrypted with $\mathsf {K\_s}$. Then, they challenge the attacker to find the encrypted data by the queries specified in Lines 41–42. The attacker can obtain the underlying data if and only if having the secret key $\mathsf {K\_s}$ since the cryptographic primitives are considered as black-boxes in ProVerif.

The second part of AKAPR ProVerif program describes the process macros for participants I, R and DG. They are specified in Lines 46–74, Lines 76–99 and Lines 101–109, respectively. These macros present the operations of I, R and DG during AKAPR execution. Note that in lines 57, 71, 86 and 98, we insert the events that we specified earlier. The other four process macros $\mathsf {processDK, processKD}$, $\mathsf {processK}$ and $\mathsf {processCTR}$ fill the four tables of secret keys defined in Lines 8–11.

In the last part of Listing 1.2, we specify the main process (Lines 127–141) of the AKAPR ProVerif program. It instantiates the keying materials needed, inserts these keys to the right tables and runs the defined macros unlimited times.

The output of the program when running with ProVerif is summarized in Listing 1.1.

The result in Lines 1–2 informs us that AKAPR provides mutual authentication of the two participants I and R. As such, the proved correspondence property in Line 1 implies that R authenticates I by the fact that I can correctly retrieve the session key $\mathsf {K_s}$. On the other hand, Line 2 shows that I authenticates R since the latter can obtain the correct ephemeral key $\mathsf {AK}$ after receiving the Message 2. In addition, Lines 3–4 show the results of the queries $\mathsf {not \, attacker(secretI[\,])}$ and $\mathsf {not \, attacker(secretR[\,])}$ returned by ProVerif. As we shall see, these results are true, which means that the secrecy of the random values $\mathsf {secretI}$ and $\mathsf {secretR}$ are preserved by the protocol. In other words, the secrecy of the session key generated by AKAPR is also preserved.

The above ProVerif verification has several limitations. Indeed, in ProVerif, the hypothesis of perfect cryptography is considered, meaning that the only way to decrypt an encrypted message is to use the right secret key. Besides, in Line 18–35, we have to model the modular multiplication and its commutative property required in the re-encryption process by defining several new functions. This is necessary because real modular multiplication cannot be handled by ProVerif. In fact, ProVerif verification might not terminate when dealing with protocols that use algebraic operations such as modular multiplication or Exclusive-or. In addition, several security protocols that are conceptually safe, but are found flawed when considering algebraic properties as described in [21]. As a result, one can complete the above formal verification using other tools such as CryptoVerif [10], CL-Atse [28] or OFMC [4], which support most of algebraic properties and provide more realistic assumptions, e.g. the hypothesis of perfect cryptography is not required.

6 Conclusion

In this paper, we first introduced a novel proxy re-encryption scheme that requires only symmetric cipher to encrypt data. We showed that although our scheme is bidirectional and single-use, it provides the most important features: non-transitivity and collusion-resistance. Furthermore, the scheme is much more efficient when compared with related solutions that use asymmetric approaches. Second, we proposed a novel authenticated delegation-based and lightweight key agreement protocol to be used in the Internet of Things. This protocol is built upon the proposed proxy re-encryption scheme. The security of our solution has been formally validated by ProVerif. In addition, thanks to the used symmetric primitives, the proposed key agreement mechanism is very lightweight since it does not require any expensive cryptographic operations such as pairing operation or modular exponentiation. The proposed protocol can be applied even in class 1 devices with extremely resource-constrained profile.

Appendix