Abstract
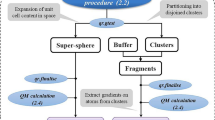
Determining the interaction strength between proteins and small molecules is key to analyzing their biological function. Quantum-mechanical calculations such as Density Functional Theory (DFT) give accurate and theoretically well-founded results. With common implementations the running time of DFT calculations increases quadratically with molecule size. Thus, numerous subsystem-based approaches have been developed to accelerate quantum-chemical calculations. These approaches partition the protein into different fragments, which are treated separately. Interactions between different fragments are approximated and introduce inaccuracies in the calculated interaction energies.
To minimize these inaccuracies, we represent the amino acids and their interactions as a weighted graph in order to apply graph partitioning. None of the existing graph partitioning work can be directly used, though, due to the unique constraints in partitioning such protein graphs. We therefore present and evaluate several algorithms, partially building upon established concepts, but adapted to handle the new constraints. For the special case of partitioning a protein along the main chain, we also present an efficient dynamic programming algorithm that yields provably optimal results. In the general scenario our algorithms usually improve the previous approach significantly and take at most a few seconds.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Andreev, K., Racke, H.: Balanced graph partitioning. Theor. Comput. Syst. 39(6), 929–939 (2006)
Buluç, A., Meyerhenke, H., Safro, I., Sanders, P., Schulz, C.: Recent advances in graph partitioning. Accepted as Chapter in AlgorithmEngineering, Overview Paper concerning the DFG SPP 1307 (2016). Preprint available at http://arxiv.org/abs/1311.3144
Clauset, A., Newman, M.E.J., Moore, C.: Finding community structure in very large networks. Phys. rev. E 70(6), 066111 (2004)
Cramer, C.J.: Essentials of Computational Chemistry. Wiley, New York (2002)
Delling, D., Fleischman, D., Goldberg, A.V., Razenshteyn, I., Werneck, R.F.: An exact combinatorial algorithm for minimum graph bisection. Math. Program. 153(2), 417–458 (2015)
Fedorov, D.G., Kitaura, K.: Extending the power of quantum chemistry to large systems with the fragment molecular orbital method. J. Phys. Chem. A 111, 6904–6914 (2007)
Fedorov, D.G., Nagata, T., Kitaura, K.: Exploring chemistry with the fragment molecular orbital method. Phys. Chem. Chem. Phys. 14, 7562–7577 (2012)
Fiduccia, C., Mattheyses, R.: A linear time heuristic for improving network partitions. In: Proceedings of the 19th ACM/IEEE Design Automation Conference, Las Vegas, NV, pp. 175–181, June 1982
Guerra, C.F., Snijders, J.G., te Velde, G., Baerends, E.J.: Towards an order-N DFT method. Theor. Chem. Acc. 99, 391 (1998)
Garey, M.R., Johnson, D.S., Stockmeyer, L.: Some simplified NP-complete problems. In: Proceedings of the 6th Annual ACM Symposium on Theory of Computing (STOC 1974), pp. 47–63. ACM Press (1974)
Ghaddar, B., Anjos, M.F., Liers, F.: A branch-and-cut algorithm based on semidefinite programming for the minimum k-partition problem. Ann. OR 188(1), 155–174 (2011)
Gordon, M.S., Fedorov, D.G., Pruitt, S.R., Slipchenko, L.V.: Fragmentation methods: a route to accurate calculations on large systems. Chem. Rev. 112, 632–672 (2012)
He, X., Zhu, T., Wang, X., Liu, J., Zhang, J.Z.H.: Fragment quantum mechanical calculation of proteins and its applications. Acc. Chem. Res. 47, 2748–2757 (2014)
Hendrickson, B., Leland, R.: A multi-level algorithm for partitioning graphs. In: Proceedings Supercomputing 1995, p. 28. ACM Press (1995)
Jacob, C.R., Neugebauer, J.: Subsystem density-functional theory. WIREs Comput. Mol. Sci. 4, 325–362 (2014)
Jacob, C.R., Visscher, L.: A subsystem density-functional theory approach for the quantumchemical treatment of proteins. J. Chem. Phys. 128, 155102 (2008)
Jensen, F.: Introduction to Computational Chemistry, 2nd edn. Wiley, Chichester (2007)
Kiewisch, K., Jacob, C.R., Visscher, L.: Quantum-chemical electron densities of proteins and of selected protein sites from subsystem density functional theory. J. Chem. Theory Comput. 9, 2425–2440 (2013)
Lanyi, J.K., Schobert, B.: Structural changes in the l photointermediate of bacteriorhodopsin. J. Mol. Biol. 365(5), 1379–1392 (2007)
Ochsenfeld, C., Kussmann, J., Lambrecht, D.S.: Linear-scaling methods in quantum chemistry. In: Lipkowitz, K.B., Cundari, T.R., Boyd, D.B. (eds.) Reviews in Computational Chemistry, vol. 23, pp. 1–82. Wiley-VCH, New York (2007)
Olsen, J.G., Flensburg, C., Olsen, O., Bricogne, G., Henriksen, A.: Solving the structure of the bubble protein using the anomaloussulfur signal from single-crystal in-house CuK\(\alpha \) diffractiondata only. Acta Crystallogr. Sect. D 60(2), 250–255 (2004)
Ormö, M., Cubitt, A.B., Kallio, K., Gross, L.A., Tsien, R.Y., Remington, S.J.: Crystal structure of the aequorea victoria green fluorescent protein. Science 273(5280), 1392–1395 (1996)
Pavlopoulos, G.A., Secrier, M., Moschopoulos, C.N., Soldatos, T.G., Kossida, S., Aerts, J., Schneider, R., Bagos, P.G.: Using graph theory to analyze biological networks. BioData Min. 4(1), 1–27 (2011)
Ramage, R., Green, J., Muir, T.W., Ogunjobi, O.M., Love, S., Shaw, K.: Synthetic, structural and biological studies of the ubiquitin system: the total chemical synthesis of ubiquitin. Biochem. J. 299(1), 151–158 (1994)
Sanders, P., Schulz, C.: Think locally, act globally: highly balanced graph partitioning. In: Bonifaci, V., Demetrescu, C., Marchetti-Spaccamela, A. (eds.) SEA 2013. LNCS, vol. 7933, pp. 164–175. Springer, Heidelberg (2013)
Staudt, C., Sazonovs, A., Meyerhenke, H.: NetworKit: an interactive tool suite for high-performance networkanalysis. CoRR, abs/1403.3005 (2014)
Tronrud, D.E., Allen, J.P.: Reinterpretation of the electron density at the site of the eighth bacteriochlorophyll in the fmo protein from pelodictyon phaeum. Photosynth. Res. 112(1), 71–74 (2012)
von Looz, M., Wolter, M., Jacob, C.,Meyerhenke, H.: Better partitions of protein graphs for subsystem quantum chemistry. Technical Report 5, Karlsruhe Institute of Technology (KIT), 3 (2016). http://digbib.ubka.uni-karlsruhe.de/volltexte/1000052814
Wesolowski, T.A., Weber, J.: Kohn-Sham equations with constrained electron density: an iterative evaluation of the ground-state electron density of interaction molecules. Chem. Phys. Lett. 248, 71–76 (1996)
Zhang, D.W., Zhang, J.Z.H.: Molecular fractionation with conjugate caps for full quantummechanical calculation of protein-molecule interaction energy. J. Chem. Phys. 119, 3599–3605 (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
von Looz, M., Wolter, M., Jacob, C.R., Meyerhenke, H. (2016). Better Partitions of Protein Graphs for Subsystem Quantum Chemistry. In: Goldberg, A., Kulikov, A. (eds) Experimental Algorithms. SEA 2016. Lecture Notes in Computer Science(), vol 9685. Springer, Cham. https://doi.org/10.1007/978-3-319-38851-9_24
Download citation
DOI: https://doi.org/10.1007/978-3-319-38851-9_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-38850-2
Online ISBN: 978-3-319-38851-9
eBook Packages: Computer ScienceComputer Science (R0)