Abstract
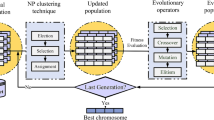
This paper presents a heuristic search-based approach for estimating the number of clusters within a dataset based on an ensemble of clustering methods. We combine a number of clustering results into near-optimal subsets using two distinct approaches. Firstly, a Gray code-based implementation evaluates the quality of all possible subsets; the quality and consistency were excellent, but the search was exhaustive, leading to exponential run-time as the volume and dimension of the dataset increased. For this reason, a Random Mutation Hill Climbing-based alternative is introduced, which evaluates the subsets in small increments, mimicking the Gray code implementation, with a minimum of ninety-two per cent accuracy (mean 96%) and a significant gain in speed (linear as opposed to exponential run-time). Our algorithms are tested on real-world and benchmark datasets, and their performance is compared to other state-of-the-art estimators with promising results. Additionally, a heuristic is presented to guide when to use the exhaustive or heuristic search.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Aggarwal, C.C., Philip, S.Y., Han, J., Wang, J.: A framework for clustering evolving data streams. In: Proceedings 2003 VLDB Conference, pp. 81–92. Elsevier (2003)
Arica, N., Yarman-Vural, F.T.: An overview of character recognition focused on off-line handwriting. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 31(2), 216–233 (2001)
Ayed, S., Arzoky, M., Swift, S., Counsell, S., Tucker, A.: An exploratory study of the inputs for ensemble clustering technique as a subset selection problem. In: Proceedings of SAI Intelligent Systems Conference, pp. 1041–1055. Springer (2018)
Charrad, M., Ghazzali, N., Boiteau, V., Niknafs, A.: NbClust: an R package for determining the relevant number of clusters in a data set. J. Stat. Softw. 61(6), 1–36 (2014). www.jstatsoft.org/v61/i06/
Doran, R.W.: The gray code. J. Univers. Comput. Sci. 13(11), 1573–1597 (2007)
Dua, D., Graff, C.: Uci machine learning repository (2017). www.archive.ics.uci.edu/ml
Elhag, A., Özcan, E.: Data clustering using grouping hyper-heuristics. In: European Conference on Evolutionary Computation in Combinatorial Optimization, pp. 101–115. Springer (2018)
Fränti, P., Sieranoja, S.: K-means properties on six clustering benchmark datasets (2018). www.cs.uef.fi/sipu/datasets/
Hamerly, G., Elkan, C.: Learning the k in k-means. In: Advances in Neural Information Processing Systems 16 (2003)
Higham, D.J., Kalna, G., Kibble, M.: Spectral clustering and its use in bioinformatics. J. Comput. Appl. Math. 204(1), 25–37 (2007)
Hubert, L., Arabie, P.: Comparing partitions. J. Classif. 2(1), 193–218 (1985)
Kass, R.E., Wasserman, L.: A reference bayesian test for nested hypotheses and its relationship to the schwarz criterion. J. Am. Stat. Assoc. 90(431), 928–934 (1995)
Kaufman, L., Rousseeuw, P.J.: Partitioning around medoids (program pam). In: Finding Groups in Data: An Introduction to Cluster Analysis, vol. 344, pp. 68–125 (1990)
Kent, J., Bibby, J., Mardia, K.: Multivariate analysis (probability and mathematical statistics) (2006)
McCarthy, M., Wiltshire, S.: Expectation maximization algorithm (e-m algorithm). Dictionary of Bioinformatics and Computational Biology (2004)
Odebode.A, Tucker.A, A.M.,S, S.: Estimating the optimal number of clusters from subsets of ensembles. In: Proceedings of the 11th International Conference on Data Science, Technology and Applications, pp. 383–391 (2022)
Pelleg, D., Moore, A.W., et al.: X-means: extending k-means with efficient estimation of the number of clusters. In: Icml, vol. 1, pp. 727–734 (2000)
Rayana, S.: ODDS library (2016). www.odds.cs.stonybrook.edu
Strehl, A., Ghosh, J.: Cluster ensembles–a knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 3(Dec), 583–617 (2002)
Swift, S., Tucker, A., Vinciotti, V., Martin, N., Orengo, C., Liu, X., Kellam, P.: Consensus clustering and functional interpretation of gene-expression data. Genome Biol. 5(11), 1–16 (2004)
Topchy, A., Jain, A.K., Punch, W.: Clustering ensembles: models of consensus and weak partitions. IEEE Trans. Pattern Anal. Mach. Intell. 27(12), 1866–1881 (2005)
Vega-Pons, S., Ruiz-Shulcloper, J.: A survey of clustering ensemble algorithms. Int. J. Pattern Recognit Artif Intell. 25(03), 337–372 (2011)
Vishnuvarthanan, G., Rajasekaran, M.P., Subbaraj, P., Vishnuvarthanan, A.: An unsupervised learning method with a clustering approach for tumor identification and tissue segmentation in magnetic resonance brain images. Appl. Soft Comput. 38, 190–212 (2016)
Zhang, Y., Zhao, Y.: Automated clustering algorithms for classification of astronomical objects. Astron. & Astrophys. 422(3), 1113–1121 (2004)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Odebode, A.A., Arzoky, M., Tucker, A., Mann, A., Maramazi, F., Swift, S. (2024). Using Clustering Ensembles and Heuristic Search to Estimate the Number of Clusters in Datasets. In: Arai, K. (eds) Intelligent Systems and Applications. IntelliSys 2023. Lecture Notes in Networks and Systems, vol 824. Springer, Cham. https://doi.org/10.1007/978-3-031-47715-7_23
Download citation
DOI: https://doi.org/10.1007/978-3-031-47715-7_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-47714-0
Online ISBN: 978-3-031-47715-7
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)