Abstract
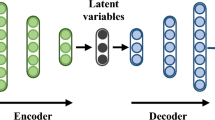
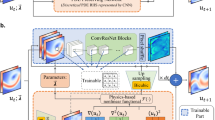
Data-driven modelling has recently gained interest in the scientific computing community with the purpose of emulating complex large scale systems. Surrogate modelling based on autoencoders (AEs) is widely employed across several engineering fields to model the time-history response of nonlinear high-dimensional dynamical systems from a set of design parameters. In this direction, this paper introduces an efficient deep learning scheme consisting of a two-steps autoencoding framework in conjunction with Neural Ordinary Differential Equations (NODEs), a novel approach for modelling time-continuous dynamics. The proposition aims at alleviating the drawbacks of similar methodologies employed for the same task, namely Parametrized NODE (PNODE) and the two-steps AE-based surrogate models, to provide a more powerful predictive tool. The effectiveness of the conceived methodology has been assessed by considering the task of emulating the spatiotemporal dynamics described by the 1D viscous Burgers’ equation. The outcomes of our empirical analysis demonstrate that our approach outperforms the alternative state-of-the-art models in terms of predictive capability.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Burgers, J.: A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199 (1948)
Chalvidal, M., Ricci, M., VanRullen, R., Serre, T.: Neural optimal control for representation learning. arXiv abs/2006.09545 (2020)
Chen, R.T.Q., Rubanova, Y., Bettencourt, J., Duvenaud, D.K.: Neural ordinary differential equations. In: Advances in Neural Information Processing Systems, vol. 31. Curran Associates, Inc. (2018)
Chen, X., et al.: Forecasting the outcome of spintronic experiments with neural ordinary differential equations. Nat. Commun. 13(1), 1016 (2022)
Dikeman, H.E., Zhang, H., Yang, S.: Stiffness-reduced neural ode models for data-driven reduced-order modeling of combustion chemical kinetics. In: AIAA SCITECH 2022 Forum, p. 0226 (2022)
Dupont, E., Doucet, A., Teh, Y.W.: Augmented neural odes. In: Advances in Neural Information Processing Systems, vol. 32 (2019)
Dupuis, R., Jouhaud, J.C., Sagaut, P.: Surrogate modeling of aerodynamic simulations for multiple operating conditions using machine learning. AIAA J. 56(9), 3622–3635 (2018)
Fresca, S., Dede’, L., Manzoni, A.: A comprehensive deep learning-based approach to reduced order modeling of nonlinear time-dependent parametrized PDEs. J. Sci. Comput. 87, 1–36 (2021)
Gergs, T., Borislavov, B., Trieschmann, J.: Efficient plasma-surface interaction surrogate model for sputtering processes based on autoencoder neural networks. J. Vac. Sci. Technol. B 40(1), 012802 (2022)
Gonzalez, F.J., Balajewicz, M.: Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems. arXiv preprint arXiv:1808.01346 (2018)
Guo, M., Hesthaven, J.S.: Reduced order modeling for nonlinear structural analysis using gaussian process regression. Comput. Methods Appl. Mech. Eng. 341, 807–826 (2018)
Hasegawa, K., Fukami, K., Murata, T., Fukagata, K.: Machine-learning-based reduced-order modeling for unsteady flows around bluff bodies of various shapes. Theoret. Comput. Fluid Dyn. 34, 367–383 (2020)
Hesthaven, J., Ubbiali, S.: Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 363, 55–78 (2018)
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. In: 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015, Conference Track Proceedings (2015)
Lazzara, M., Chevalier, M., Colombo, M., Garcia, J.G., Lapeyre, C., Teste, O.: Surrogate modelling for an aircraft dynamic landing loads simulation using an LSTM autoencoder-based dimensionality reduction approach. Aerosp. Sci. Technol. 126, 107629 (2022)
Lee, K., Parish, E.J.: Parameterized neural ordinary differential equations: applications to computational physics problems. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 477(2253), 20210162 (2021)
Maulik, R., Lusch, B., Balaprakash, P.: Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders. Phys. Fluids 33(3), 037106 (2021)
Maulik, R., Mohan, A., Lusch, B., Madireddy, S., Balaprakash, P., Livescu, D.: Time-series learning of latent-space dynamics for reduced-order model closure. Physica D 405, 132368 (2020)
Milan, P.J., Torelli, R., Lusch, B., Magnotti, G.: Data-driven model reduction of multiphase flow in a single-hole automotive injector. At. Sprays 30(6) (2020)
Na, J., Jeon, K., Lee, W.B.: Toxic gas release modeling for real-time analysis using variational autoencoder with convolutional neural networks. Chem. Eng. Sci. 181, 68–78 (2018)
Nakamura, T., Fukami, K., Hasegawa, K., Nabae, Y., Fukagata, K.: Convolutional neural network and long short-term memory based reduced order surrogate for minimal turbulent channel flow. Phys. Fluids 33(2), 025116 (2021)
Nikolopoulos, S., Kalogeris, I., Papadopoulos, V.: Non-intrusive surrogate modeling for parametrized time-dependent partial differential equations using convolutional autoencoders. Eng. Appl. Artif. Intell. 109, 104652 (2022)
Portwood, G.D., et al.: Turbulence forecasting via neural ODE. arXiv preprint arXiv:1911.05180 (2019)
Rahman, S.M., Pawar, S., San, O., Rasheed, A., Iliescu, T.: Nonintrusive reduced order modeling framework for quasigeostrophic turbulence. Phys. Rev. E 100, 053306 (2019)
Raviv, L., Lupyan, G., Green, S.C.: How variability shapes learning and generalization. Trends Cogn. Sci. 26(6), 462–483 (2022)
Rubanova, Y., Chen, R.T., Duvenaud, D.K.: Latent ordinary differential equations for irregularly-sampled time series. In: Advances in Neural Information Processing Systems, vol. 32 (2019)
Salvador, M., Dede, L., Manzoni, A.: Non intrusive reduced order modeling of parametrized PDEs by kernel pod and neural networks. Comput. Math. Appl. 104, 1–13 (2021)
Sekar, V., Jiang, Q., Shu, C., Khoo, B.C.: Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 31(5), 057103 (2019)
Shankar, V., et al.: Learning non-linear spatio-temporal dynamics with convolutional neural odes. In: Third Workshop on Machine Learning and the Physical Sciences (NeurIPS 2020) (2020)
Sharif, S.A., Hammad, A., Eshraghi, P.: Generation of whole building renovation scenarios using variational autoencoders. Energy Build. 230, 110520 (2021)
Tenenbaum, J.B., Griffiths, T.L.: Generalization, similarity, and bayesian inference. Behav. Brain Sci. 24(4), 629640 (2001)
Thangamuthu, A., Kumar, G., Bishnoi, S., Bhattoo, R., Krishnan, N.M.A., Ranu, S.: Unravelling the performance of physics-informed graph neural networks for dynamical systems. In: Thirty-sixth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (2022)
Wang, J., He, C., Li, R., Chen, H., Zhai, C., Zhang, M.: Flow field prediction of supercritical airfoils via variational autoencoder based deep learning framework. Phys. Fluids 33(8), 086108 (2021)
Wang, Z., Xiao, D., Fang, F., Govindan, R., Pain, C.C., Guo, Y.: Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Meth. Fluids 86(4), 255–268 (2018)
Xu, J., Duraisamy, K.: Multi-level convolutional autoencoder networks for parametric prediction of spatio-temporal dynamics. Comput. Methods Appl. Mech. Eng. 372, 113379 (2020)
Acknowledgement
This work has been supported by Airbus Operations SAS and the French National Agency for Technological Research (ANRT) within the CIFRE framework (grant N\(^o\) 2019/1815).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Lazzara, M., Chevalier, M., Lapeyre, C., Teste, O. (2023). NeuralODE-Based Latent Trajectories into AutoEncoder Architecture for Surrogate Modelling of Parametrized High-Dimensional Dynamical Systems. In: Iliadis, L., Papaleonidas, A., Angelov, P., Jayne, C. (eds) Artificial Neural Networks and Machine Learning – ICANN 2023. ICANN 2023. Lecture Notes in Computer Science, vol 14259. Springer, Cham. https://doi.org/10.1007/978-3-031-44223-0_40
Download citation
DOI: https://doi.org/10.1007/978-3-031-44223-0_40
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-44222-3
Online ISBN: 978-3-031-44223-0
eBook Packages: Computer ScienceComputer Science (R0)