Abstract
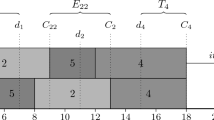
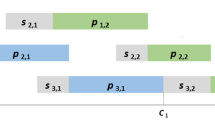
In this paper, three configurations of the customer order scheduling problem are presented. In contrast to classical scheduling problems, the customer order scheduling problem considers the scheduling of jobs that belong to customer orders and each order is only completed when each job of the order has finished. The studied configurations are the minimization of the sum of order completion times and the minimization of the earliness-tardiness in a machine environment where each order places one job on each machine. Furthermore, the minimization of the sum of order completion times in a flow shop environment is investigated. This paper states properties of the three problem configurations and describes developed solution methods that performed well in a computational experiment.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Framinan, J. M., & Perez-Gonzalez, P. (2017). New approximate algorithms for the customer order scheduling problem with total completion time objective. Computers and Operations Research, 78, 181–192. https://doi.org/10.1016/j.cor.2016.09.010
Leung, J. Y. -T., Li, H., & Pinedo, M. (2005) Order scheduling in an environment with dedicated resources in parallel. Journal of Scheduling, 8(5), 355–386. https://doi.org/10.1007/s10951-005-2860-x
Zipfel, B., Neufeld, J. S., & Buscher, U. (2021). Customer order scheduling in an additive manufacturing environment. In A. Dolgui, A. Bernard, D. Lemoine, G. von Cieminski & Romero, D. (Eds.), Advances in production management systems. Artificial intelligence for sustainable and resilient production systems. APMS 2021. IFIP advances in information and communication technology (Vol. 633, pp. 101–109). Springer, Cham. https://doi.org/10.1007/978-3-030-85910-7_11
Sung, C. S., & Yoon, S. H. (1998). Minimizing total weighted completion time at a preassembly stage composed of two feeding machines. International Journal of Production Economics, 54(3), 247–255. https://doi.org/10.1016/S0925-5273(97)00151-5
Leung, J. Y. T., Lee, C., Ng, C., & Young, G. (2008). Preemptive multiprocessor order scheduling to minimize total weighted flowtime. European Journal of Operational Research, 190(1), 40–51. https://doi.org/10.1016/j.ejor.2007.05.052
Framinan, J. M., & Perez-Gonzalez, P. (2018). Order scheduling with tardiness objective: Improved approximate solutions. European Journal of Operational Research, 266(3), 840–850. https://doi.org/10.1016/j.ejor.2017.10.064
Zhao, Z., Zhou, M., & Liu, S. (2022). Iterated greedy algorithms for flow-shop scheduling problems: A tutorial. IEEE Transactions on Automation Science and Engineering, 19(3), 1941–1959. https://doi.org/10.1109/TASE.2021.3062994
Nawaz, M., Enscore, E. E., & Ham, I. (1983). A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega, 11(1), 91–95. https://doi.org/10.1016/0305-0483(83)90088-9
Framinan, J. M., & Leisten, R. (2008). Total tardiness minimization in permutation flow shops: A simple approach based on a variable greedy algorithm. International Journal of Production Research, 46(22), 6479–6498. https://doi.org/10.1080/00207540701418960
Wu, C. C., Yang, T. H., Zhang, X., Kang, C. C., Chung, I. H., & Lin, W. C. (2019). Using heuristic and iterative greedy algorithms for the total weighted completion time order scheduling with release times. Swarm and Evolutionary Computation, 44, 913–926. https://doi.org/10.1016/j.swevo.2018.10.003
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Hoffmann, J. (2023). Solving Customer Order Scheduling Problems with an Iterated Greedy Algorithm. In: Grothe, O., Nickel, S., Rebennack, S., Stein, O. (eds) Operations Research Proceedings 2022. OR 2022. Lecture Notes in Operations Research. Springer, Cham. https://doi.org/10.1007/978-3-031-24907-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-24907-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-24906-8
Online ISBN: 978-3-031-24907-5
eBook Packages: Business and ManagementBusiness and Management (R0)