Abstract
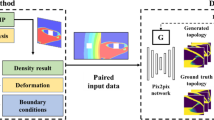
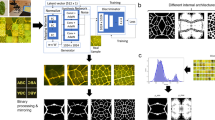
Topology optimization is a powerful tool for producing an optimal free-form design from input mechanical constraints. However, in its traditional-density-based approach, it does not feature a proper definition for the external boundary. Therefore, the integration of shape-related constraints remains hard. It requires the experts’ intervention to interpret the generated designs into parametric shapes; thus, making the design process time-consuming. With the growing role of additive manufacturing in the industry, developing a design approach considering mechanical and geometrical constraints simultaneously becomes an interesting way to integrate manufacturing and aesthetics constraints into mechanical design. In this paper, we propose to generate mechanically and geometrically valid designs using a deep-learning solution trained via a dual-discriminator Generative Adversarial Network (GAN) framework. This Deep-learning-geometrical-driven solution generates designs very similar to traditional topology optimization’s outputs in a fraction of time.
Moreover, it allows an easy shape fine-tuning by a simple increase/decrease of the input geometrical condition (here the total-bar-count), a task that a traditional topology optimization cannot achieve.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
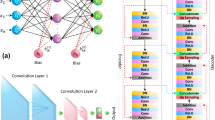
The architecture of the residual unit block used in this work is detailed in [32].
- 2.
The stem and inception/reduction blocks used defers from the original paper [27] only by the number of input/output feature maps.
- 3.
This code is available on the GitHub repository: https://github.com/dbetteb/TOP_OPT.git.
- 4.
A loaded node \(n_e\) located at line \(i\) and column \(j\) tilted \(\theta \) degrees has \(F_x(i,j) = cos(\theta )\) and \(F_y(i,j) = sin(\theta )\); the magnitude of the loads were set to \(1.0\) \(N\).
- 5.
A fixed bar is a bar where boundary conditions are applied. A loaded bar is a bar where a load is applied.
References
Abueidda, D.W., Koric, S., Sobh, N.A.: Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 237, 106283 (2020)
Adam, G.A., Zimmer, D.: Design for additive manufacturing–element transitions and aggregated structures. CIRP J. Manuf. Sci. Technol. 7(1), 20–28 (2014)
Allaire, G., Jouve, F., Toader, A.M.: A level-set method for shape optimization. Comput. R. Math. 334(12), 1125–1130 (2002)
Bendsøe, M.P.: Optimal shape design as a material distribution problem. Struct. optim. 1(4), 193–202 (1989)
Bendsøe, M.P., Sigmund, O.: Material interpolation schemes in topology optimization. Arch. Appl. Mech. 69(9–10), 635–654 (1999)
Bi, S., Zhang, J., Zhang, G.: Scalable deep-learning-accelerated topology optimization for additively manufactured materials. arXiv preprint arXiv:2011.14177 (2020)
Goodfellow, I., et al.: Generative adversarial nets. In: Advances in Neural Information Processing Systems, pp. 2672–2680 (2014)
Guo, Y., Liu, Y., Oerlemans, A., Lao, S., Wu, S., Lew, M.S.: Deep learning for visual understanding: a review. Neurocomputing 187, 27–48 (2016)
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778 (2016)
Hoyer, S., Sohl-Dickstein, J., Greydanus, S.: Neural reparameterization improves structural optimization. arXiv preprint arXiv:1909.04240 (2019)
Kallioras, N.A., Kazakis, G., Lagaros, N.D.: Accelerated topology optimization by means of deep learning. Struct. Multi. Optim. 62(3), 1185–1212 (2020)
Leary, M., Merli, L., Torti, F., Mazur, M., Brandt, M.: Optimal topology for additive manufacture: a method for enabling additive manufacture of support-free optimal structures. Mater. Des. 63, 678–690 (2014)
Li, S., Yuan, S., Zhu, J., Wang, C., Li, J., Zhang, W.: Additive manufacturing-driven design optimization: building direction and structural topology. Add. Manuf. 36, 101406 (2020)
Malviya, M.: A systematic study of deep generative models for rapid topology optimization (2020)
Mass, Y., Amir, O.: Topology optimization for additive manufacturing: accounting for overhang limitations using a virtual skeleton. Add. Manuf. 18, 58–73 (2017)
Mirza, M., Osindero, S.: Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014)
Nie, Z., Lin, T., Jiang, H., Kara, L.B.: Topologygan: topology optimization using generative adversarial networks based on physical fields over the initial domain. arXiv preprint arXiv:2003.04685 (2020)
Radford, A., Metz, L., Chintala, S.: Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434 (2015)
Rawat, S., Shen, M.H.H.: A novel topology optimization approach using conditional deep learning. arXiv preprint arXiv:1901.04859 (2019)
Rawat, W., Wang, Z.: Deep convolutional neural networks for image classification: a comprehensive review. Neural Comput. 29(9), 2352–2449 (2017)
Ronneberger, O., Fischer, P., Brox, T.: U-Net: convolutional networks for biomedical image segmentation. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 234–241. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24574-4_28
Sharpe, C., Seepersad, C.C.: Topology design with conditional generative adversarial networks. In: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, vol. 59186, p. V02AT03A062. American Society of Mechanical Engineers (2019)
Sigmund, O.: A 99 line topology optimization code written in matlab. Struct. Mult. Optim. 21(2), 120–127 (2001)
Sigmund, O., Petersson, J.: Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 16(1), 68–75 (1998)
Sosnovik, I., Oseledets, I.: Neural networks for topology optimization. Russ. J. Numer. Anal. Math. Modell. 34(4), 215–223 (2019)
Subedi, S.C., Verma, C.S., Suresh, K.: A review of methods for the geometric post-processing of topology optimized models. Journal of Computing and Information Science in Engineering, vol. 20, no. 6 (2020)
Szegedy, C., Ioffe, S., Vanhoucke, V., Alemi, A.A.: Inception-v4, inception-resnet and the impact of residual connections on learning. In: Thirty-First AAAI Conference on Artificial Intelligence (2017)
Ulu, E., Zhang, R., Kara, L.B.: A data-driven investigation and estimation of optimal topologies under variable loading configurations. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 4(2), 61–72 (2016)
Wang, C., Qian, X.: Simultaneous optimization of build orientation and topology for additive manufacturing. Add. Manuf. 34, 101246 (2020)
Yu, Y., Hur, T., Jung, J., Jang, I.G.: Deep learning for determining a near-optimal topological design without any iteration. Struct. Multi. Optim. 59(3), 787–799 (2018). https://doi.org/10.1007/s00158-018-2101-5
Zhang, W., Zhou, L.: Topology optimization of self-supporting structures with polygon features for additive manufacturing. Comput. Methods Appl. Mech. Eng. 334, 56–78 (2018)
Zhang, Z., Liu, Q., Wang, Y.: Road extraction by deep residual u-net. IEEE Geosci. Remote Sens. Lett. 15(5), 749–753 (2018)
Zhao, Z.Q., Zheng, P., Xu, S.T., Wu, X.: Object detection with deep learning: a review. IEEE Trans. Neural Netw. Learn. Syst. 30(11), 3212–3232 (2019)
Acknowledgement
This work was supported by Expleo France.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Almasri, W., Bettebghor, D., Ababsa, F., Danglade, F., Adjed, F. (2021). Deep Learning Architecture for Topological Optimized Mechanical Design Generation with Complex Shape Criterion. In: Fujita, H., Selamat, A., Lin, J.CW., Ali, M. (eds) Advances and Trends in Artificial Intelligence. Artificial Intelligence Practices. IEA/AIE 2021. Lecture Notes in Computer Science(), vol 12798. Springer, Cham. https://doi.org/10.1007/978-3-030-79457-6_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-79457-6_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79456-9
Online ISBN: 978-3-030-79457-6
eBook Packages: Computer ScienceComputer Science (R0)