Abstract
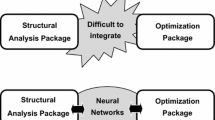
In this study, Differential Evolution, a powerful metaheuristic algorithm, is employed to optimize the weight of truss structures. One of the major challenges of all metaheuristic algorithms is time-consuming where a large number of structural analyses are required. To deal with this problem, neural networks are used to quickly evaluate the response of the structures. Firstly, a number of data points are collected from a parametric finite element analysis, then the obtained datasets are used to train neural network models. Secondly, the trained models are utilized to predict the behavior of truss structures in the constraint handling step of the optimization procedure. Neural network models are developed using Python because this language supports many useful machine learning libraries such as scikit-learn, tensorflow, keras. Two well-known benchmark problems are optimized using the proposed approach to demonstrate its effectiveness. The results show that using neural networks helps to greatly reduce the computation time.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Rajeev, S., Krishnamoorthy, C.S.: Discrete optimization of structures using genetic algorithms. J. Struct. Eng. 118(5), 1233–1250 (1992)
Beyer, H.G.: The Theory of Evolution Strategies. Springer, Heidelberg (2001). https://doi.org/10.1007/978-3-662-04378-3s
Price, K.V., Storn, R.M., Lampien, J.A.: Differential Evolution: A Practical Approach to Global Optimization. Springer, Heidelberg (2005). https://doi.org/10.1007/3-540-31306-0
Eberhart, R., Kennedy, J.: Particle swarm optimization. In: Proceedings of ICNN 1995-International Conference on Neural Networks, vol. 4, pp. 1942–1948. IEEE (1995)
Dorigo, M., Stützle, T.: Ant Colony Optimization. MIT Press, Cambridge (2004)
Karaboga, D.: An idea based on honey bee swarm for numerical optimization. Technical report - TR06, vol. 200, pp. 1–10 (2005)
Latif, M.A., Saka, M.P.: Optimum design of tied-arch bridges under code requirements using enhanced artificial bee colony algorithm. Adv. Eng. Softw. 135, 102685 (2019)
Papadrakakis, M., Lagaros, N.D., Tsompanakis, Y.: Optimization of large-scale 3-D trusses using evolution strategies and neural networks. Int. J. Space Struct. 14(3), 211–223 (1999)
Kaveh, A., Gholipour, Y., Rahami, H.: Optimal design of transmission towers using genetic algorithm and neural networks. Int. J. Space Struct. 23(1), 1–19 (2008)
Krempser, E., Bernardino, H.S., Barbosa, H.J., Lemonge, A.C.: Differential evolution assisted by surrogate models for structural optimization problems. In: Proceedings of the international conference on computational structures technology (CST), vol. 49. Civil-Comp Press (2012)
Penadés-Plà, V., García-Segura, T., Yepes, V.: Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 179, 556–565 (2019)
Vesterstrom, J., Thomsen, R.: A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In: Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753), Portland, USA, vol. 2, pp. 1980–1987. IEEE (2004)
Hieu, N.T., Tuan, V.A.: A comparative study of machine learning algorithms in predicting the behavior of truss structures. In: Proceeding of the 5th International Conference on Research in Intelligent and Computing in Engineering RICE 2020. Springer (2020). (accepted for publication)
Storn, R., Price, K.: Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11(4), 341–359 (1997)
Lampinen, J.: A constraint handling approach for the differential evolution algorithm. In: Proceedings of the 2002 Congress on Evolutionary Computation (IEEE Cat. No. 02TH8600), Portland, USA, vol. 2, pp. 1468–1473. IEEE (2002)
Goodfellow, I., Bengio, Y., Courville, A.: Deep Learning. MIT Press, Cambridge (2016)
Rumelhart, D.E., Hinton, G.E., Williams, R.J.: Learning representations by back-propagating errors. Nature 323(6088), 533–536 (1986)
Differential Evolution Code Homepage. https://www.icsi.berkeley.edu/~storn/code.html. Accessed 28 Jan 2020
PyNiteFEA Homepage. https://pypi.org/project/PyNiteFEA/. Accessed 22 Apr 2020
Keras Document Homepage. https://keras.io/. Accessed 22 Apr 2020
Lee, S., Ha, J., Zokhirova, M., Moon, H., Lee, J.: Background information of deep learning for structural engineering. Arch. Comput. Meth. Eng. 25(1), 121–129 (2018)
Du, F., Dong, Q.Y., Li, H.S.: Truss structure optimization with subset simulation and augmented Lagrangian multiplier method. Algorithms 10(4), 128 (2017)
Acknowledgment
This work was supported by the Domestic Ph.D. Scholarship Programme of Vingroup Innovation Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Nguyen, TH., Vu, AT. (2020). Using Neural Networks as Surrogate Models in Differential Evolution Optimization of Truss Structures. In: Nguyen, N.T., Hoang, B.H., Huynh, C.P., Hwang, D., Trawiński, B., Vossen, G. (eds) Computational Collective Intelligence. ICCCI 2020. Lecture Notes in Computer Science(), vol 12496. Springer, Cham. https://doi.org/10.1007/978-3-030-63007-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-63007-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-63006-5
Online ISBN: 978-3-030-63007-2
eBook Packages: Computer ScienceComputer Science (R0)