Speckle Reduction for Fourier Ptychographic Reconstruction Using Gamma-Correction and Reshaped Wirtinger Flow Optimization

Abstract

Fourier ptychography is a newly reported computational imaging technique, which is used for long-distance, sub-diffraction imaging recently. Compared to conventional Fourier ptychographic microscopy, there is pronounced laser speckle noise in captured images. In this work, a new framework is proposed to suppress speckle noise and reconstruct the high-resolution image for diffuse object. We introduce a random phase to simulate the effects of rough surface during imaging process, and then recover the high-resolution spectrum following two steps: the first is to promote the noisy captured images using Gamma-correction, and the second step is to recover the Fourier spectrum using reshaped Wirtinger flow optimization. Experiments on both simulation and real data demonstrate that the proposed method incorporates speckle noise reduction into reconstruction process, which can achieve better results on both visual and quantitative metrics compared to previous work.

1 Introduction

Fourier Ptychography (FP) is a novel method to improve spatial resolution in microscopy, which can beyond the diffraction-limit of objective lens. This technique illuminates the target with different angels, and correspondingly captures multiple low-resolution images describing different spatial spectrum bands of the target. By stitching these spectrum bands together in the Fourier space, the entire high-resolution spatial spectrum can be reconstructed, including both phase and amplitude [1, 2]. Recently, initial work in macroscopic imaging suggests that FP has potential benefits in improving spatial resolution for long-distance imaging [3]. Holloway et al. demonstrate that Fourier ptychography can dramatically improve the resolution of stand-off scenery and their experiments show resolution gains of are achievable [4]. The following research of them proposes FP for diffuse objects could produce speckle on the image plane, which deteriorates perceptual quality of the recovered high-resolution image [5]. There are two methods to suppress speckle noise including optical processing and digital image processing. Optical processing reduces the speckle noise by reducing the spatial coherence of laser beams or diversifying the wavelength and angle [6, 7]. Digital image processing is also important for the suppression of speckle. Several algorithms have been proposed for reducing speckle such as wavelet-based transformations [8], Lee-filter [9], nonlocal means algorithm [10], etc. Besides, the recent research [11] shows that gamma-correction of noisy hologram can affect the speckle noise reduction effect, which does not introduce a lot of computational complexity.

In fact, Fourier ptychography can reduce the speckle size by reducing diffraction blur. Thus, an effective reconstruction algorithm is also important for suppressing speckle noise. Mathematically, FP can be considered as a typical phase retrieval optimization process, which aims to recover the complex high-resolution spatial spectrum. Alternating projection (AP) [12] is a phase retrieval algorithm, which has been widely used in conventional Fourier ptychography including the latest macroscopic Fourier ptychography. AP algorithm is easy to use and converges quickly, but is sensitive to measurement noise. Wirtinger flow optimization for Fourier Ptychography (WFP) is a novel application of Wirtinger Flow optimization proposed by Bian [13, 14], which minimizes the intensity error between estimated low-resolution images and corresponding measurements using the gradient scheme and Wirtinger calculus [15]. Zhang et al. propose a reshaped Wirtinger flow approach for solving quadratic system of equations [16]. The experiments demonstrate this lower-order loss function based on absolute magnitude has great advantages in statistical and computational efficiency compared to Wirtinger Flow optimization. Here this optimization algorithm is first used for Fourier ptychographic reconstruction and we call it Reshaped-WFP (reshaped Wirtinger flow optimization for Fourier Ptychography).

Based on previous work, a new framework is proposed to reduce the effects of speckle noise and improve quality of the reconstructed high-resolution image. The advantages of our work are three aspects: A random optical phase is introduced to simulate the effects of rough surface toward long-distance imaging using FP; Gamma-correction is used as data preprocessing for captured low-resolution images to suppress the speckle noise; Reshaped Wirtinger flow optimization for Fourier Ptychography (Reshaped-WFP) is implemented as the reconstruction algorithm to retrieval the high-resolution spatial spectrum, which can increase peak signal to noise ratio (PSNR) and reduce relative error (RE).

2 Methods

2.1 Image Formation Model for Diffuse Objects

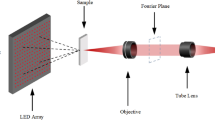
Most real-world objects are ‘optically rough’ on the scale of optical wavelength. The surface of them has many microscopic scattering points fluctuating randomly. Each point along the surface acts as a secondary source when coherent light illuminates the object. These secondary light sources scattering from the points interfere with each other to produce speckle on the image plane [17]. The speckle overlaps with the image and distorts the recovered results, which should be suppressed for laser illumination imaging. The roughness of object’s surface plays a decisive role in speckle phenomenon. It can be described by three important parameters including root mean square (rms) height, correlation length of surface height and rms slope. These parameters depict statistical characteristics of the surface height, which can uniquely determine the roughness of surface. As a preliminary simulation study, only rms height and rms slope are taken into consideration to simulate the rough surface here. Besides, the Gaussian distribution is important to describe surface scattering models because it is suitable for most scenarios. The target is considered as an ideal smooth model with a rough surface following Gaussian distribution, as shown in Fig. 1. The laser beam with center $\lambda$ wavelength illuminates the object located at the coordinate plane $r_{0}$ and scatters. The complex amplitude of optical field in the Fraunhofer plane $r^{\prime}$ can be described as

Fig. 1.

The schematic diagram of speckle field produced by surface scattering in the Fraunhofer plane.

$$ U\left( {r'} \right) = \int {\psi \left( {r_{0} } \right)} \exp (\frac{{ - i4\pi z\left( {r_{0} } \right)}}{\lambda }\exp (\frac{{ - i2\pi r_{0} \cdot r'}}{\lambda z})dr_{0} $$

(1)

where $\psi (r_{0} )$ denotes illuminated field emerging from the smooth object, $z(r_{0} )$ is the height function of random surface following Gauss distribution, ${{4\pi z(r_{0} )} \mathord{\left/ {\vphantom {{4\pi z(r_{0} )} \lambda }} \right. \kern-0pt} \lambda }$ is the optical phase and is the distance between observation plane and scattering surface. Specially, a phase function $\exp ({{ - i4\pi z(r_{0} )} \mathord{\left/ {\vphantom {{ - i4\pi z(r_{0} )} \lambda }} \right. \kern-0pt} \lambda })$ is introduced to simulate the scattering for random rough surface. We could change the variance $\sigma_{z}^{2}$ of height function to control the roughness of objects.

We describe our camera aperture using the pupil function $P(x^{\prime},y^{\prime})$, which can be considered as an ideal low-pass filter. $(x^{\prime},y^{\prime})$ are the 2D spatial frequency coordinates in the Fraunhofer plane. Since optical field is limited by camera aperture, the light field immediately after the aperture is given by product $U(r^{\prime})P(x^{\prime},y^{\prime})$. This band limited optical field then propagates to the image plane and is recorded by camera sensor.

$$ I(x,y) = \left| {F^{ - 1} \left[ {U(r^{\prime})P(x^{\prime},y^{\prime})} \right]} \right|^{2} $$

(2)

where $I(x,y)$ is a simulated image with laser speckle noise, $(x,y)$ are the 2D spatial frequency coordinates in the image plane, and $F^{ - 1}$ denotes the inverse Fourier transform.

Then we recenter the camera in Fourier plane at $m$ different locations $(c_{x'} (i),c_{{y^{\prime}}} (i)),i = 1,2, \cdots m$. From previous work, adequate reconstruction results can be achieved when two adjacent positions satisfy the overlap ratio of 65% or more [1]. The final series of low-resolution images can be given as

$$ I_{i} (x,y) = \left| {F^{ - 1} \left[ {U(r^{\prime})P(x^{\prime} - c_{{x^{\prime}}} (i),y^{\prime} - c_{{y^{\prime}}} (i))} \right]} \right|^{2} $$

(3)

2.2 Data Preprocessing Using Gamma-Correction

Gamma-correction is a simple and efficient method to suppress speckle noise in holographic imaging [11]. Here, it is extended to fourier ptychography framework to preprocess the captured images. The scattering of the rough surface can change the polarization state of the incident light and the probability distribution of speckle image’s intensity is described as

$$ p(I_{i} ) = 4\frac{{I_{i} }}{{\mu^{2} }}\exp ( - 2\frac{{I_{i} }}{\mu })\,\,\,\,\,\,\,\,\,\,\, \, for \, I_{i} \ge 0 $$

(4)

where $\mu$ is the mean intensity. Equation (5) is the Fourier transform of Eq. (4)

$$ F(\omega ) = \frac{1}{2 + j\mu \omega } $$

(5)

From the Eq. (5), it is clear that the Fourier transform curve becomes smooth with decrease of $\mu$. The Gamma-correction used to suppress the intensity of speckle noise can be given as

$$ I_{pi} = cI_{i}^{\Gamma } $$

(6)

where $I_{i}$ is the normalized intensity of original captured image, $I_{pi}$ is the image after Gamma-correction and $c$ is a positive constant. We use a $512px \times 512px$ ‘Lena’ image shown in Fig. 2(a) as the measured images with strong speckle noise $\sigma_{z}^{2} { = 0} . 1 4$. Figure 2(b) is the normalized intensity distribution after gamma-correction with ${\Gamma} = 1.2$. It can be seen that the intensity distribution of target becomes steeper using gamma-correction, which means the number of low gray values increased and the number of high gray values reduced. Thus, the mean intensity $\mu$ of noisy image is also reduced in this transformation. The Fourier transform function curve after gamma-correction becomes smoother, so the contrast of the FFT transformation is lower than before. It’s very beneficial for reconstruction which can be verified by following experiments.

Fig. 2.

(a) A simulated image with laser speckle noise. (b) Normalized intensity distribution of (a) using Gamma-correction.

However, the imaging objects and noise intensity are unknown for most applications. Obtaining the reasonable value of $\Gamma$ which can fit most real situations is crucial for the preprocessing step. To address this problem, we first estimate the variance of captured images and then calculate the $\Gamma$ based on it. From the Subsect. 2.1, it can be seen that $I_{i}$ is a series of low resolution images corrupted with diffraction blur and speckle noise. Estimating the variance of all images is inapplicable because it requires high computation cost. Then the center image is selected to estimate the value of $\Gamma$. Speckle can be regarded as multiplicative noise following negative exponential distribution [17]. To estimate speckle noise level, the natural logarithm of the captured center image is taken to convert the noise into a more convenient additive model $\xi_{c} = \ln (I_{c} )$. Here the new variable $\xi_{c}$ is modeled as a noise-free signal $\xi_{c}^{\prime }$ corrupted by additive noise $\eta$, which can be described as $\xi_{c} = \xi_{c}^{\prime } + \eta$. Specifically, $\eta$ is signal-independent additive noise with zero mean and $\sigma_{\eta }^{2}$ variance. A novel method to estimate the noise level of $\xi_{c}$ is based on principal component analysis (PCA) of image blocks, which has higher computational efficiency and better accuracy compared with other methods. From the previous research [18], the m smallest eigenvalues of $\Sigma _{{\xi_{c} }}$ equal $\sigma_{\eta }^{2}$ if the information in noise-free image $\xi_{c}^{\prime }$ is redundant. Where $\Sigma _{{\xi_{c} }}$ is the population covariance matrices of $\xi_{c}$. Then the value of $\Gamma$ can be computed by

$$ {\Gamma} = \,k\sigma_{\eta }^{2} + b $$

(7)

A large number of experiments indicate that the reasonable value of ranges from 1 to 1.25. In this work, $k = 1{\text{ and }}b = 1.07$ can fit the most scenes. Figure 3(a) provides six test images and Fig. 3(b) provides $\Gamma$ value of them under different speckle noise level.

Fig. 3.

(a) Six test images. (b) The estimated $\Gamma$ value for test images with different speckle noise level.

2.3 Reshaped-WFP Optimization

To obtain the high-resolution image, we use Reshaped-WFP optimization to recover the high resolution complex field in the aperture plane. Reshaped Wirtinger flow is a recently reported algorithm to recover a vector $x$ based on the magnitude measurements $y = \left\{ {\left| {\left\langle {a_{i} ,x} \right\rangle } \right|} \right\}_{i = 1}^{m}$ and the design vectors $\left\{ {a_{i} } \right\}_{i = 1}^{m}$. It solves the problem by minimizing the nonconvex loss function via a gradient algorithm, and enjoys geometric convergence to a global optimal as long as the number of measurements is at the order of $O(n)$, where $n$ is the dimension of $x$. In this work, we extend the Reshaped Wirtinger flow optimization to fourier ptychographic reconstruction algorithm. Here the high resolution spectrum of target is considered as the vector of interest, fourier ptychographic imaging process is considered as the design vectors, and the captured images after gamma-correction are taken as the magnitude measurements. Then the loss function is given as

$$ \hbox{min} \, f(\hat{U}) = \frac{1}{2m}\sum\limits_{i = 1}^{m} {(\left| {A_{i} \hat{U}} \right| - \sqrt {I_{pi} } )^{2} } $$

(8)

the gradient of the loss function is

$$ \nabla f(\hat{U}) = \frac{1}{m}\sum\limits_{i = 1}^{m} {(A_{i} \hat{U} - \sqrt {I_{pi} } \cdot \text{sgn} (A_{i} \hat{U}))} A_{i}^{T} = \frac{1}{m}\sum\limits_{i = 1}^{m} {(A_{i} \hat{U} - \sqrt {I_{pi} } \cdot \frac{{A_{i} \hat{U}}}{{\left| {A_{i} \hat{U}} \right|}})} A_{i}^{T} $$

(9)

In implementation, $\hat{U}$ can be solved in a descending manner as

$$ \hat{U}^{(t + 1)} = \hat{U}^{(t)} - \frac{\mu }{m}\sum\limits_{i = 1}^{m} {(A_{i} \hat{U} - \sqrt {I_{pi} } \cdot \frac{{A_{i} \hat{U}}}{{\left| {A_{i} \hat{U}} \right|}})} A_{i}^{T} $$

(10)

where $\mu$ is the gradient descent step size set by user and plural vector $\hat{U} \in {\mathbb{C}}^{n}$ denotes the high resolution spatial spectrum we need. Specifically, $A_{i}$ corresponds to the imaging process of Eq. (3) which is composed of two components including inverse fourier transform $F^{ - 1}$ and down sampling of pupil $P(x^{\prime} - c_{{x^{\prime}}} (i),y^{\prime} - c_{{y^{\prime}}} (i))$.

The proposed reconstruction algorithm is summarized as Algorithm 1.

3 Experiments

In this section, a series of experiments are conducted on both simulation and real data, to demonstrate the performance of proposed algorithm.

3.1 Experiment on Simulation Data

In order to better fit the real situation, the sub-imaging setup parameters are set as follows. The illumination wavelength is 632.8 nm, the focal length of the lens is 75 mm and the aperture diameter is 2.3 mm which corresponds to an ideal pupil function (all ones in the pupil circle and all zeros outside). Similar to the research [14], the overlap ratio between two adjacent pictures is set to be $\xi = 65\%$. We use the $512px \times 512px$ ‘Lena’ image from the USC-SIPI image database [19] as ground truth and the pixel size of captured images is 2.2 um. The number of horizontal and vertical measurements is $m = 15 \times 15$. The captured LR images’ pixel numbers are set to be one fifth of the reconstruction image along both dimensions, and are obtained according to Eq. (3).

Based on the above parameter settings and Fourier ptychography imaging method, the simulation of our sub-diffraction imaging process is synthesized by the following steps: (1) Adding rough surface to the ground truth image to simulate a diffuse object. (2) We perform the FFT transformation on the obtained image and pick out the corresponding sub-region by multiplying it with the pupil function. (3) Translating the pupil to capture different regions of the Fourier domain and get a series of noisy images with limited spectrum. (4) Gamma-correction of these low resolution images to initially suppress the intensity

In addition to visual effects, two quantitative evaluation criteria are adopted to objectively evaluate the quality of algorithms. The first one is peak signal to noise ratio (PSNR), which is widely used to assess the image quality after processing. It can intuitively describe the intensity difference between two images, and would be greater for higher quality image. Another criterion is relative error (RE) [20], which is given as

$$ RE(z,\hat{z}) = \frac{{\min_{\phi \in [0,2\pi )} \left\| {e^{ - j\phi } z - \hat{z}} \right\|^{2} }}{{\left\| {\hat{z}} \right\|^{2} }} $$

(11)

It is mainly used to measure the difference between two complex functions $z{\text{ and }}\hat{z}$, here to compare the recovered spectrum with original spectrum. The RE scores range from 0 to 1, and is smaller for higher quality recovery.

To demonstrate the performance and advantages of proposed algorithm, a series of experiments are simulated on synthetic data. We compare our algorithm with the AP algorithm, which is also used in research [4, 5] to recover the image with speckle noise for long-distance, sub-diffraction imaging. Here the update of pupil function does not be considered for simplicity. The fluctuation of object’s surface follows Gaussian distribution, and the variance $\sigma_{z}^{2}$ of height function ranges from 0.08 to 0.16. With the increase of variance $\sigma_{z}^{2}$, the surface roughness of object increases and the speckle noise becomes more pronounced. By algorithm testing, the number of iterations is set to 300 to ensure the convergence of proposed algorithm.

The quantitative results are shown in Fig. 4(a) and (b). It is clear that the qualities of reconstructed images degrade with the increase of surface roughness, the PSNR becomes smaller and the RE becomes larger. However, the proposed algorithm has obvious advantages in PSNR and RE for different levels of speckle noise compared to AP. It can raise PSNR by almost 5 dB and reduce RE by almost 0.3, even in strong noise levels. Besides, the reconstruction quality of our algorithm does not degenerate a lot with the increase of surface roughness. This demonstrates the robustness of proposed method to laser speckle noise, and thus it has a wider application value toward long-distance Fourier Ptychography reconstruction. Figure 5 provides the visual reconstruction results, and the variance is fixed at 0.10. Figure 5(a) is one of the captured images simulated by the proposed framework, which is hardly to recognize due to speckle noise corruption. Figure 5(b) and (c) are recovered high-resolution amplitude images using AP and the proposed algorithm, respectively. There is a lot of speckle in Fig. 5(b) because AP is sensitive to measurement noise. Figure 5(c) is of higher quality than Fig. 5(b), which can remove most of noise without losing crucial high frequency details. This is because the proposed algorithm incorporates speckle noise reduction into the reconstruction process. The convergence rate of above methods is shown in Fig. 5(d) and (e). It demonstrates that our proposed algorithm could obtain a good result in the fiftieth iteration, and converge within 200 iterations. There is no great difference in convergence speed compared with AP. Therefore, the proposed algorithm could obtain satisfying reconstruction quality with less speckle noise and more image details, which outperform the AP on both visual and quantitative results.

Fig. 4.

(a) Quantitative comparison for the PSNR (dB) at different speckle noise levels. (b) Quantitative comparison for the RE at different speckle noise levels.

Fig. 5.

Comparison of the reconstruction results. (a) Original image (b) Simulated acquisition image. (c) The reconstructed image using AP. (d) The reconstructed image using proposed algorithm. (e) The convergence rate of different methods for PSNR. (f) The convergence rate of different methods for RE

3.2 Experiment on Real Data

To further verify the performance of proposed algorithm, we use the real data set from research [4] as initial input images (http://jrholloway.com/projects/towardCCA). The scene is a translucent Dasani water bottle label and we only intercept part of them, as shown in Fig. 6. Due to the roughness surface, this diffuse water bottle label has a random phase which can produce a highly varying optical field at the image plane, and thus the captured images contain laser speckle noise. The real data set is captured by the setup with 81% overlap between adjacent images. The number of horizontal and vertical measurements is 17 and other parameters are the same as those in simulation process. Figure 6(a) is the center image of the data set, which is degraded by speckle and diffraction blur. Figure 6(b) and (c) are reconstruction intensity images using AP and the proposed algorithm respectively. Compared to AP, our algorithm can remove some of the artifacts and reduce the contrast of speckle as shown in Fig. 6(c). Figure 6(d) and (e) are detail regions of Fig. 6(b) and (c), which can be seen that the proposed algorithm has lower speckle compared to AP in visual.

Fig. 6.

Reconstruction comparison on real data set. (a) The center image of real data set. (b) The recovered intensity image using AP. (c) The recovered intensity image using proposed algorithm. (d) The detail region of (b). (e) The detail region of (c).

4 Conclusions and Discussions

This paper proposes a new reconstruction framework for long-distance, sub-diffraction imaging using Fourier ptychography, which aims to reduce the speckle noise produced by diffuse objects. Compared to previous FP implementations, a randomly distributed phase is introduced to obtain noisy images with different levels of speckle. Then we use Gamma-correction as data preprocessing, which can preliminary suppress speckle noise without large computational complexity. Based on the recently reported reshaped Wirtinger flow optimization, we recover the high resolution spectrum as solving quadratic system of equations, and present a solution utilizing the gradient descent scheme. The results demonstrate that proposed algorithm can get better quantitative and visual effects compared to AP algorithm which is mainly used in this field now. Specially, the recovered image with less noise and more details can be achieved because no filter is used during the reconstruction. From the previous research, Fourier ptychographic imaging for long distance has potential significance in many computer vision and imaging applications including remote sensing and surveillance. However, Speckle noise and the robustness of reconstruction algorithm are main barriers to build a real system. This work solves these problems and will help a lot to realize a full-scale implementation.